--- type: slide tags: MANDELBROT,fractales title: 2024 centenaire MANDELBROT DIMENSION autoSlide: 10 slideOptions: defaultTiming: 20 transition: slide progress: true parallaxBackgroundImage: "https://minio.apps.education.fr/codimd-prod/uploads/upload_c6279aa629a6bf4c65c455cb593234d1.jpg" --- # 2024 centenaire MANDELBROT ## dimensions fractales  --- ## Dimensions 1,2,3,4! 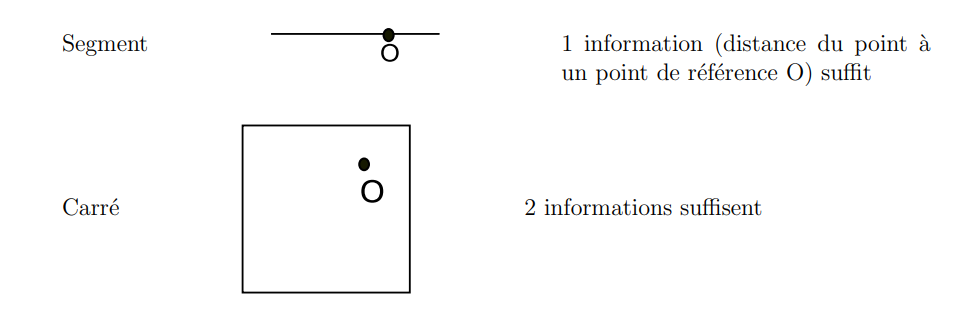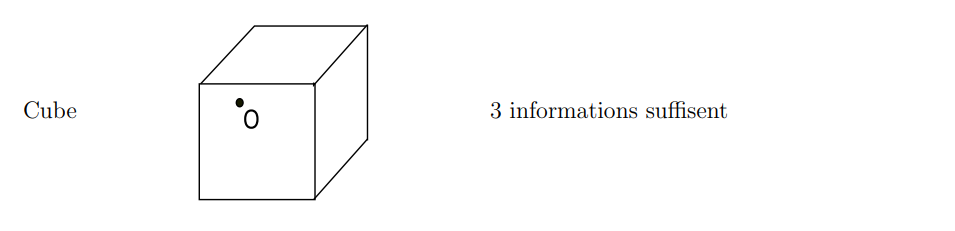{%youtube ShvJVdNMCUg %} --- dimension fractale {%youtube eKY_1j9VrEA %} --- {%youtube gB9n2gHsHN4 %} ---- Aller à 4:40 {%youtube iFA3g_4myFw %} ---- LECTURE CONSEILLEE Le monde fascinant des objets fractals -- Florence Messineo (PEANO) https://laboutique.edpsciences.fr/produit/952/9782759820924/les-fractales-en-images/preview?escape=false#lg=1&slide=0(bd) --- ## Dimension On a l’habitude de penser à la notion de dimension en termes de degrés de liberté (nombre de directions indépendantes ou nombre d’informations nécessaires pour localiser un point). 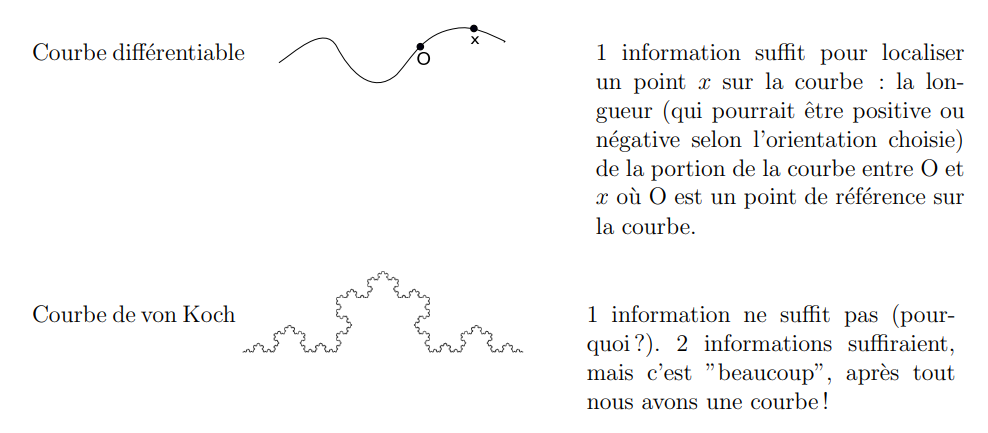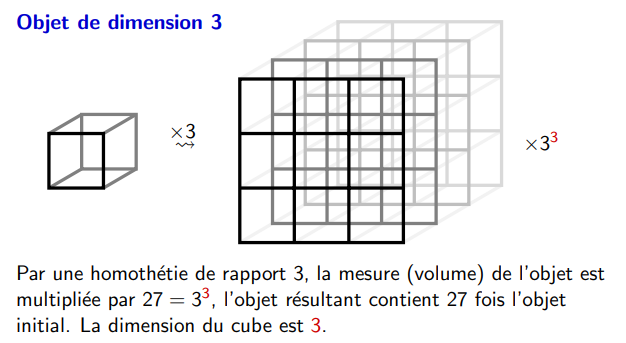---   ---  --- Il y a une autre façon de voir la dimension ---  ---  --- Peu importe le facteur d'agrandissement/reduction s, on aura toujours $N = s^d$ , où $d$ est la dimension. 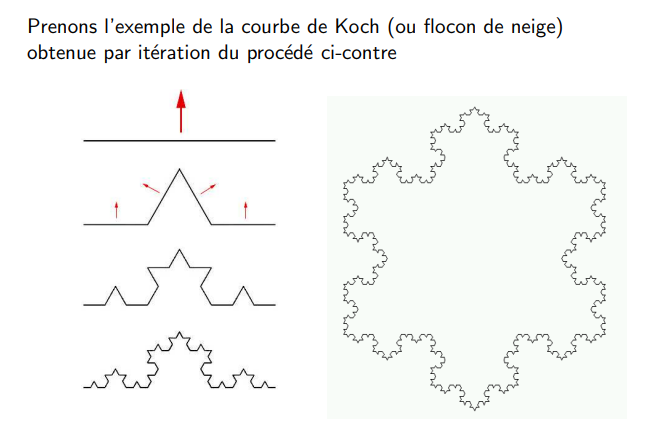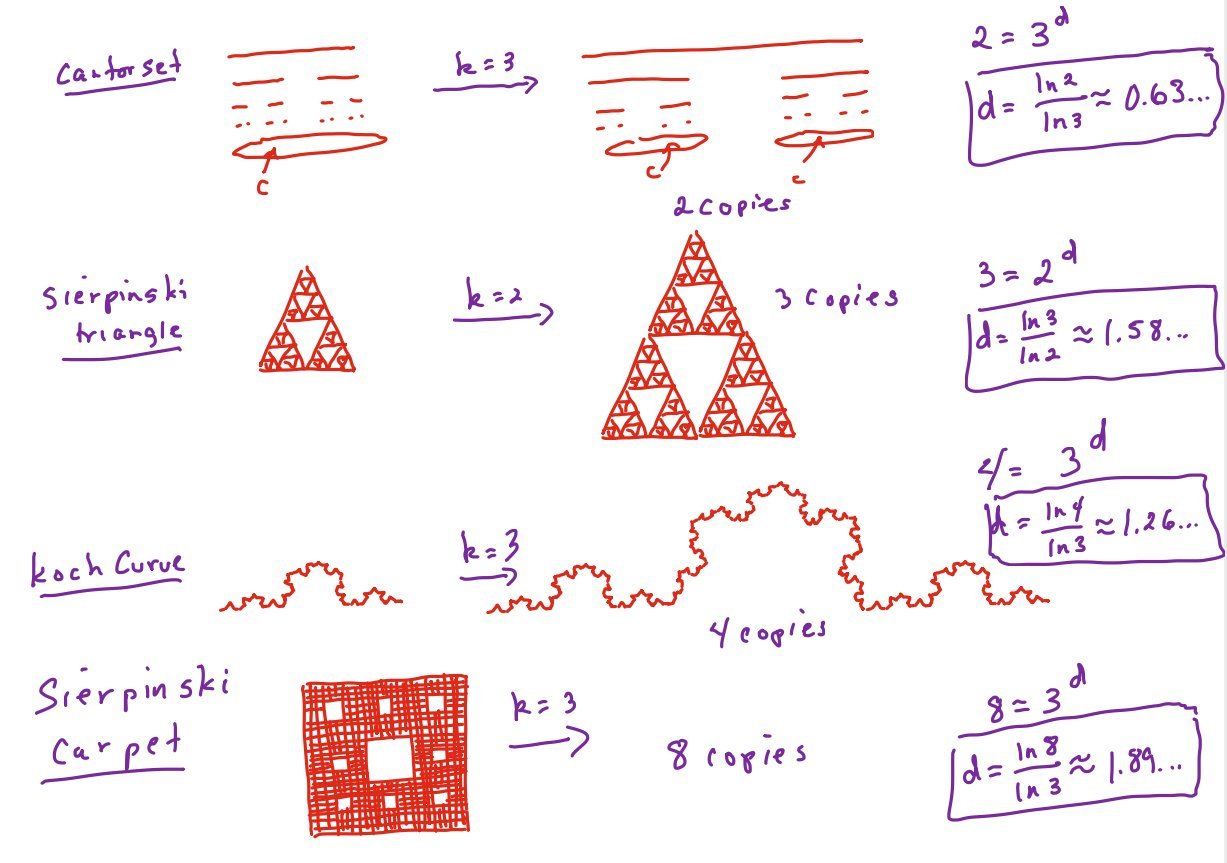L’égalité $N = s^d$ s’écrit aussi sous la forme $d = \frac{log N }{log s}$ ---  ---  --- ## poussière de Cantor  Par une homothétie de rapport 3, l’objet devient un objet de nature identique, contenant 2 morceaux de même taille que l’objet initial, donc de mesure 2 fois plus grande. 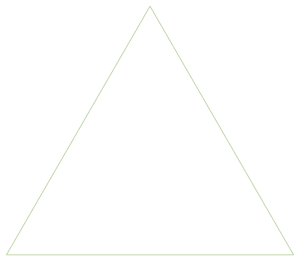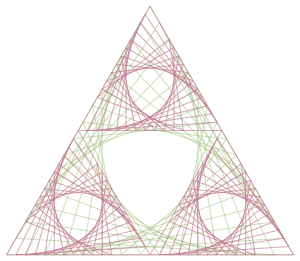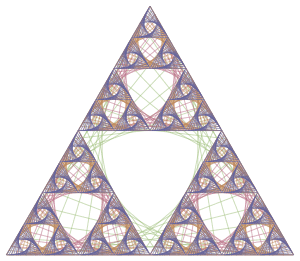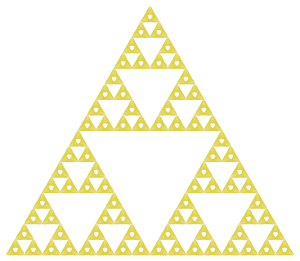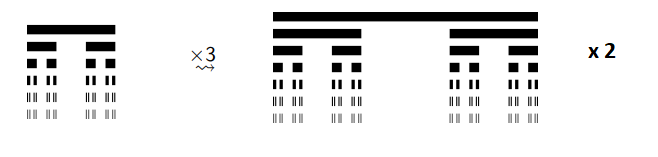Ceci conduit à poser$3^d=2$ soit $d=\frac{ln(3)} {ln(2)} \approx 0,63$ --- ## Tapis de Sierpinski  Par une homothétie de rapport 3, l’objet devient un objet de nature identique, contenant 8 morceaux de même taille que l’objet initial, donc de mesure 8 fois plus grande. Ceci conduit à poser$3^d=8$ soit $d=\frac{ln(8)} {ln(2)} \approx = 1,89$ --- ## éponge de Menger  Par une homothétie de rapport 3, l’objet devient un objet de nature identique, contenant 20 morceaux de même taille que l’objet initial, donc de mesure 20 fois plus grande. Ceci conduit à poser$3^d=20$ soit $d=\frac{ln(20)} {ln(3)} \approx = 2,73$ --- ## Dimension de Bouligand. Imaginons que l’on veuille calculer la dimension d’un objet fractal qui n’a pas de similitude interne comme par exemple la côte de la Grande Bretagne. L’idée est de recouvrir cet objet par une maille carrée de plus en plus fine et de ne compter que les carrés qui recouvrent l’objet. 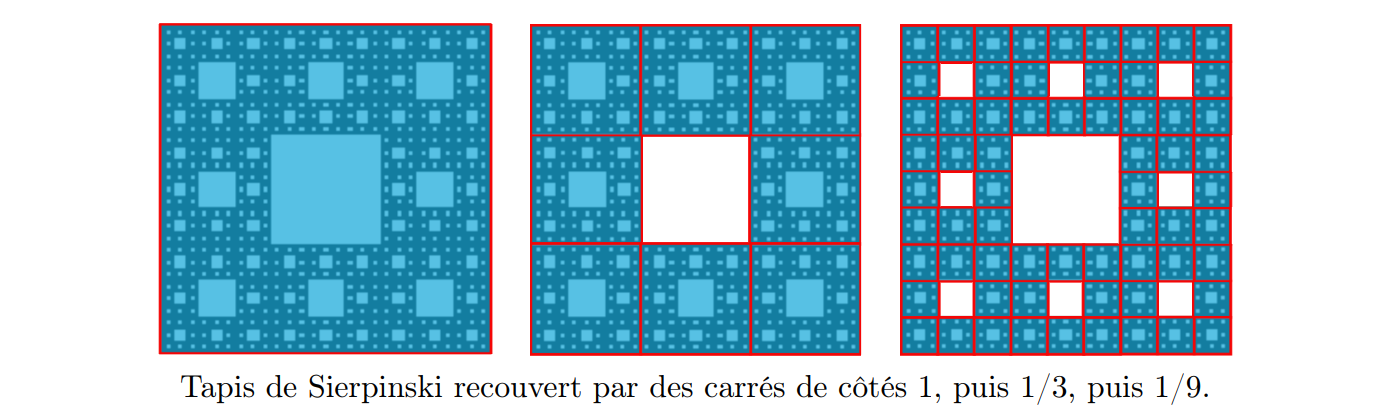Commençons à appliquer ce procédé au tapis de Sierpinski pour voir que l’on retrouve bien la valeur précédemment calculée d =ln(8)/ln(3) . ---- On recouvre avec un carré initial, disons de côté 1, puis par 8 carrés de côté 1/3, puis avec des côtés de $(1/3)^2$ il en faut $8 \times 8 = 8^2$ , et ainsi de suite. Il faudra 8^n carrés de côtés $(1/3)^n$. ---- Pour passer d’un petit carré de côté 1/3 n au carré unitaire initial, il faut le multiplier par son inverse : $3^n$. Lorsqu’on effectue cet agrandissement on obtient la figure initiale qui comporte donc $8^n$ copies de ce petit carré. D’après notre formeule précédente on obtient donc une dimension fractale pour le tapis de Sierpinski qui vaut : $$\frac{ln(8^n)}{ln(3^n)}=\frac{n ln(8)}{n ln(3)} =\frac{ln(8)}{ln(3)}$$ ---  ---- Et on retrouve exactement la valeur précédemment calculée. Dans ce cas, cela ne dépend pas de la taille des côtés des carrés choisis, à cause de la propriété de similitude interne du tapis de Sierpinski. On généralise alors cette méthode pour calculer par exemple la dimension fractale de la côte de la Grande Bretagne : On recouvre l’île par une maille carrée dont les côtés sont de plus en plus petits. ---- Alors par analogie avec le calcul précédent, on considère que l’objet est localement à similitude interne : si les carrés sont de côtés ε alors c’est en appliquant un agrandissement de 1/ε qu’on obtient le carré de longueur 1 et on peut estimer que chacun de ces petits carrés est une miniature d’un carré de côté 1. Si on note Nε le nombre de carrés nécessaires au recouvrement de la côte, sa dimension fractale sera pour ε assez petit : $d ≈\frac{ln(Nε)}{ln(1/ε)}$ ----  On compte le nombre Nε de carrés de côtés ε pour recouvrir la côte de la Grande Bretagne. 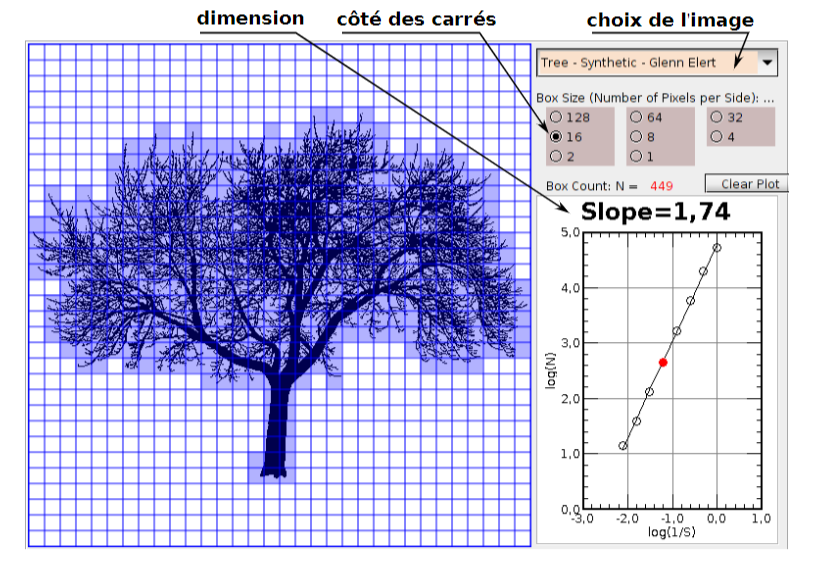Pour ε assez petit, la dimension fractale est environ $\frac{ln(Nε)}{ln(1/ε)}$ ---- Son avantage est de pouvoir se prêter à des calculs effectifs (par ordinateur) du comptage de carrés, donnant une valeur approchée de la dimension de n’importe quelle fractale dont on a une image. ---- $d = \frac{ln(Nε)}{ln(1/ε)}$ "équivaut à" $Nε = C × (\frac{1}{ε})^d$ où C est une constante Avec le logarithme, cela donne: $$ln(Nε) = d\times ln(1/ε)+ln(C)$$ --- Autrement dit en posant Y = ln(Nε) et X = ln(1/ε) cette relation est de la forme Y = dX + C c’est à dire que le graphique de Y = ln(Nε) en fonction de X = ln(1/ε) doit donner une droite dont la pente est la dimension cherchée : d. En pratique on utilise un logiciel qui trace un maillage carré sur la figure fractale, compte les carrés la recouvrant et place un point sur le graphique pour chaque taille de carrés choisie. On calcule alors la pente de la droite qui nous donne d. 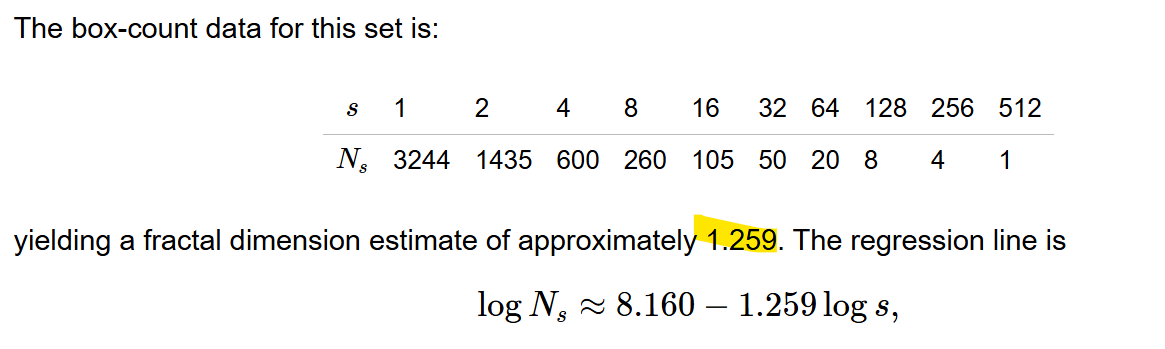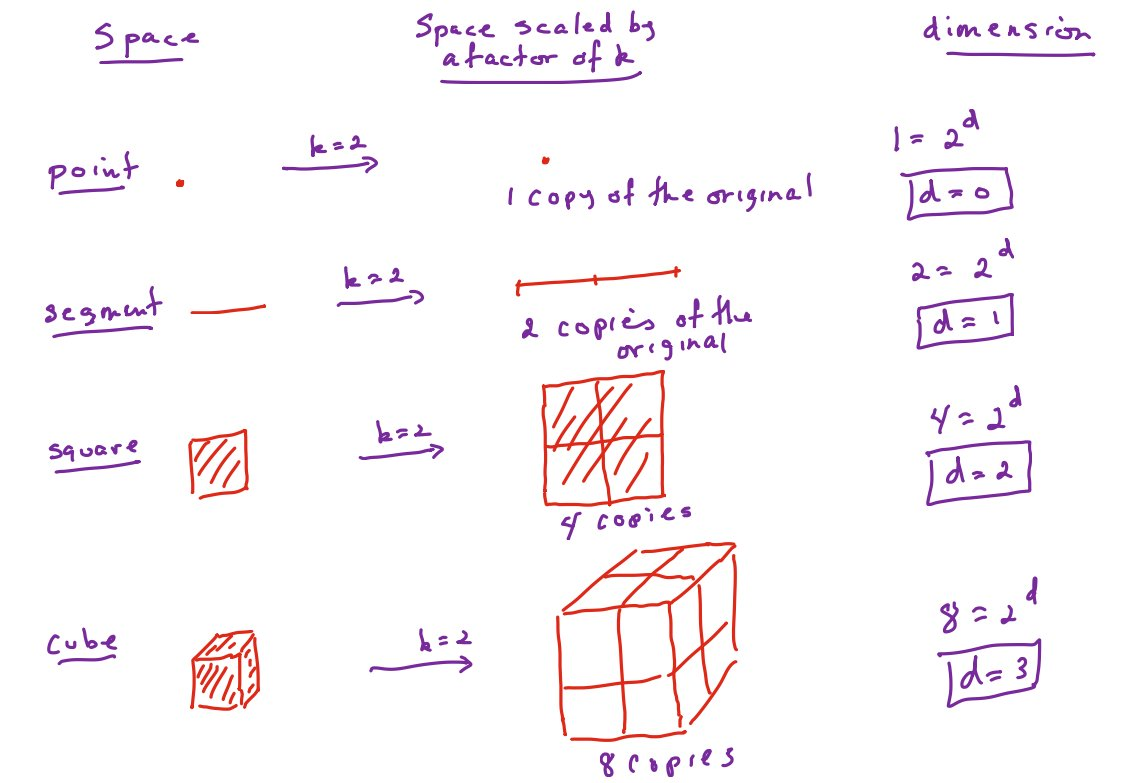---- http://prof.pantaloni.free.fr/IMG/pdf/Dimension-dim-fractale.pdf  ---- https://marksmath.org/visualization/box_counter.html   --- https://nuage03.apps.education.fr/index.php/s/etW5sJ9z2HENbGi ---  ---  --- https://twitter.com/mathemaniac/status/1251570400200294402 --- <iframe width="100%" height="500" src="https://depot-e.uqtr.ca/id/eprint/1565/1/000135084.pdf#page=95" > </iframe> --- <iframe width="100%" height="500" src="https://pedagogie.ac-orleans-tours.fr/fileadmin/user_upload/maths/Autres_ressources_pour_la_classe/Rubrique_%C3%A0_Brac/Atelierfractales2.pdf" > </iframe> --- []( https://www.yumpu.com/fr/document/read/39652233/dimensions-fractales-kafemath)