--- type: slide tags: diapo, nderiv, derivée, rdvm #mots clefs title: 'Le nombre dérivé - RDVM dida' #Changer le titre ici slideOptions: transition: concave #convex-out theme: white #moon night blood # Pour avoir le logo académique sur chaque diapo. Autre version sans "-corps-inspection" parallaxBackgroundImage: 'https://minio.apps.education.fr/codimd-prod/uploads/b098212450fcfc51583a71a52.png' parallaxBackgroundSize: 100% parallaxBackgroundHorizontal: 0 parallaxBackgroundVertical: 0 parallaxBackgroundRepeat: no-repeat # Les diapositives commencent ci-dessous --- <!-- Image avec le logo académique & insp maths: 'https://minio.apps.education.fr/codimd-prod/uploads/b098212450fcfc51583a71a52.png' Logo académique uniquement : 'https://minio.apps.education.fr/codimd-prod/uploads/b098212450fcfc51583a71a5a.png' --> # Le nombre dérivé ### Rendez-vous des matheux #rdvm #### Didactique lycée *Mercredi 21 mai 2025* Les ressources rdvm accessibles via [dgxy.link/rdvm](https://dgxy.link/rdvm) <!-- Marmit  --> --- ## Plan ### Première partie - généralités * Enjeux * Histoire * Anti-problème * S'adapter aux différents niveaux --- ## Plan ### Deuxième partie - Exemples * Maths spécifique * Maths en voie techno * Spé maths * Exemple 1 * Exemple 2 * Jigsaw * Bilan, pièges didactiques. --- ### I. 1. Enjeux * notion phare du programme d’analyse au lycée * nécessite une bonne maîtrise de nombreux concepts en amont * étape cruciale pour une bonne compréhension des problèmes de variation * prépare à l'analyse du supérieur (notion de DL) ----  ---- ### I. 1. 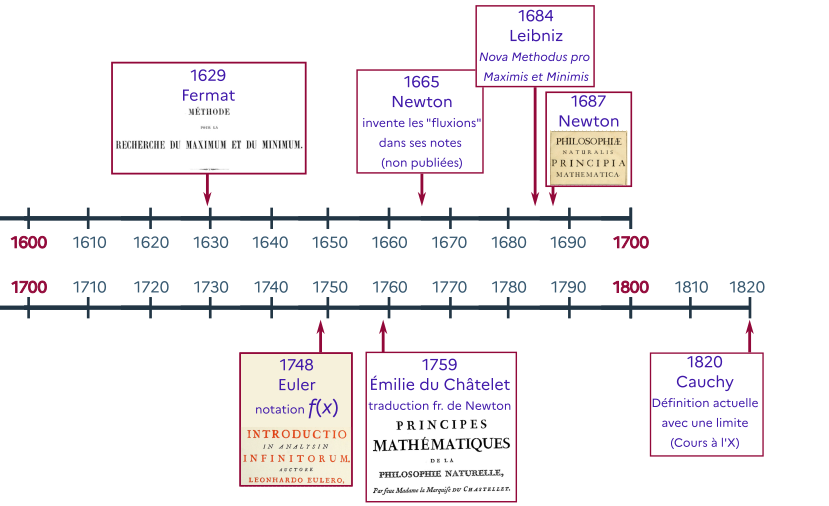Enjeux  --- ### I. 2. Histoire  #### Chronologie <i class="fa fa-chevron-down" aria-hidden="true"></i> ----  ---- <!-- .slide: data-background="https://minio.apps.education.fr/codimd-prod/uploads/96c2186ec322d4d78a95d16bf.png"--> ----  https://journals.openedition.org/bibnum/610 ---- <iframe scrolling="no" title="Rectangle d'aire maximale à périmètre fixé" src="https://www.geogebra.org/material/iframe/id/tnw7qt2s/width/714/height/425/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="714px" height="425px" style="border:0px;"> </iframe> https://www.geogebra.org/m/vyfanbdq --- ### I. 3. Anti-problème : Comment bien rater sa présentation du nombre dérivé ? C'est quand même simple, non ? $f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$ <!-- Remettre les $$ ensuite, ça fait sauter la coloration syntaxique --> ----  [www.maths-et-tiques.fr/telech/Nombrederive.pdf](https://www.maths-et-tiques.fr/telech/Nombrederive.pdf) ---- ### Quelles difficultés ? * Taux de variation mal connu ; * Coefficient directeur mal connu ; * Première rencontre de la notion de limite ; * Beaucoup de lettres ; * Première rencontre de la notion de tangente ; * Aucune notion de régularité des fonctions ; * Peu de fonctions de référence connues. --- ## Deuxième partie - Exemples ### S'adapter aux différents niveaux * Maths spécifique * Maths en voie techno * Spé maths * Exemple 1 * Exemple 2 --- ### Nombre dérivé en maths spécifiques <img src="https://minio.apps.education.fr/codimd-prod/uploads/96c2186ec322d4d78a95d1656.png" width="30%"> <img src="https://minio.apps.education.fr/codimd-prod/uploads/96c2186ec322d4d78a95d1676.png" width="66%"> https://www.geogebra.org/m/gjkggufr Courbe de croissance et tangente. <i class="fa fa-chevron-down" aria-hidden="true"></i> Ressource éduscol. 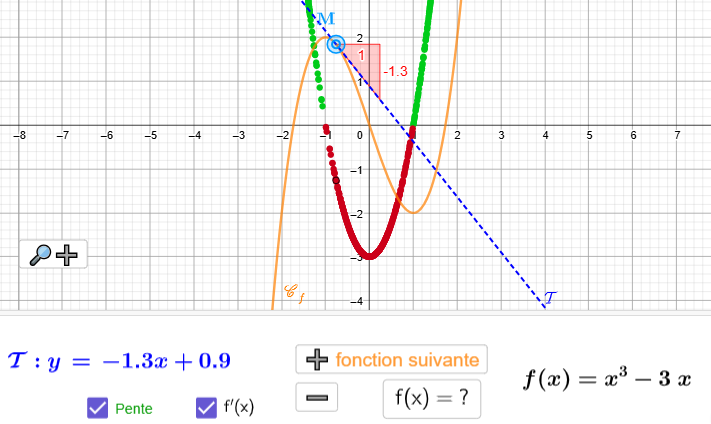---- <iframe src="https://www.geogebra.org/m/gjkggufr#material/ejybzqtk" style="width:1000px;height:550px;border=2px" ></iframe> ---- #### Lien avec le sens de variation <iframe src="https://www.geogebra.org/m/gjkggufr#material/qaq377pq" style="width:1000px;height:500px" ></iframe> ---- #### Fonction dérivée  https://www.geogebra.org/m/c4sjqjbz <i class="fa fa-chevron-down" aria-hidden="true"></i> ---- <iframe src="https://www.geogebra.org/m/c4sjqjbz" style="width:1000px;height:500px" ></iframe> --- ### Nombre dérivé en voie techno. #### Automatismes et origami <!-- .slide: data-background="https://minio.apps.education.fr/codimd-prod/uploads/cfd629a2a56fbb4614f5b228e.png"--> > <i class="fa fa-id-card-o" aria-hidden="true"></i> Nicolas Rency, formateur. Enseignant agrégé au lycée Jacques Coeur, Bourges (18). ---- #### Les attentes du programme  ---- #### Les attentes du programme  ---- #### Les attentes du programme  ---- #### Objectif : Enrichir le modèle de fonction pour permettre de nouvelles études. En milieu de classe de 1re, un élève voit la représentation graphique d’une fonction comme un modèle choisi d’interpolation de points dont les coordonnées ont été calculées. Pour étudier les variations d’une fonction, il faudrait donc mener une étude systématique point par point ou s’appuyer sur les seules fonctions de référence. ---- #### Objectif : Enrichir le modèle de fonction La courbe représentative d’une fonction suffisamment régulière est aussi l’enveloppe de ses tangentes. ⇒ Origami sur le modèle MVA ---- ##### Définition d’une parabole comme enveloppe La parabole de foyer $F$ et de directrice donnée est l’enveloppe des médiatrices des segments $[FH]$, $H$ décrivant la directrice. <img src="https://minio.apps.education.fr/codimd-prod/uploads/cfd629a2a56fbb4614f5b22c4.png" width="40%"> https://www.geogebra.org/m/bav9cjgc <i class="fa fa-chevron-down" aria-hidden="true"></i> ---- <iframe scrolling="no" title="Parabole comme enveloppe de droite - origami" src="https://www.geogebra.org/material/iframe/id/q5df6fwd/width/866/height/465/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="866px" height="465px" style="border:0px;"> </iframe> ---- #### Réalisations avec des élèves  ---- #### Réalisations avec des élèves  ---- #### Réalisations avec des élèves <img src="https://minio.apps.education.fr/codimd-prod/uploads/cfd629a2a56fbb4614f5b22c7.png" width="60%"> ---- #### Qu'en retiennent les élèves ?  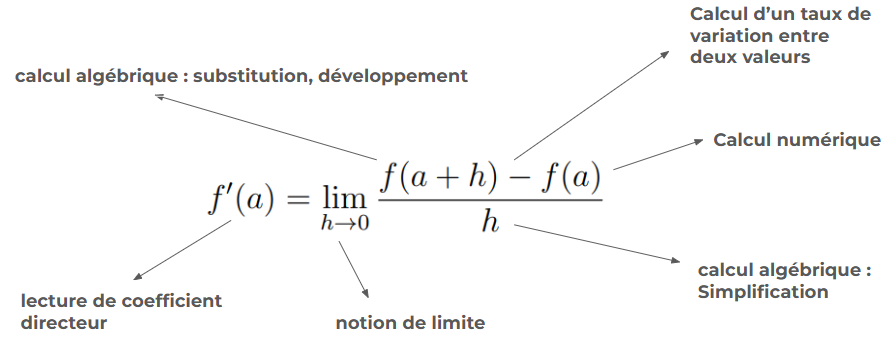---- #### Vers une institutionnalisation : subdiviser les tâches  ---- #### Vers une institutionnalisation : s’appuyer sur les automatismes  ---- #### Vers une institutionnalisation : s’appuyer sur les automatismes  ---- #### Vers une institutionnalisation : s’appuyer sur les automatismes  ---- #### Equation de la tangente En 1re techno, les textes ne spécifient pas la forme de la formule. Là encore c’est l’occasion de ré-investir les automatismes “Déterminer l’équation réduite” d’une droite, à partir de la donnée : * du coefficient directeur (aka le nombre dérivé de $f$ en $a$) * des coordonnées du point de contact $A(a,f(a))$. --- ### Nombre dérivé en spé maths #### Exemple 1 - Chute libre #### Exemple 2 - Excès de vitesse --- ### Nombre dérivé en spé maths #### Exemple 1 - Chute libre 💡Idée : estimer une vitesse (instantanée) au point d'impact après une chute libre. https://www.geogebra.org/m/mqt9wz4k <i class="fa fa-chevron-down" aria-hidden="true"></i> ---- Animation pour lancer l'activité. **Q:** *Vitesse au point d'impact ?* <img src="https://www.geogebra.org/resource/wwafb4hk/j0DOIe2dJOD3o6RI/material-wwafb4hk.png" width="45%"> ---- Animation ggb <iframe scrolling="no" title="Introduction au nombre dérivé." src="https://www.geogebra.org/material/iframe/id/xephzgqx/width/1239/height/677/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/false" width="1239px" height="677px" style="border:0px;"> </iframe> ---- Pièges et difficultés : * à gauche le point B descend, sur le graphique il monte. * vitesse mesurée en m/s * Tous les élèves ne sont pas à l'aise avec la notion de vitesse (moyenne). 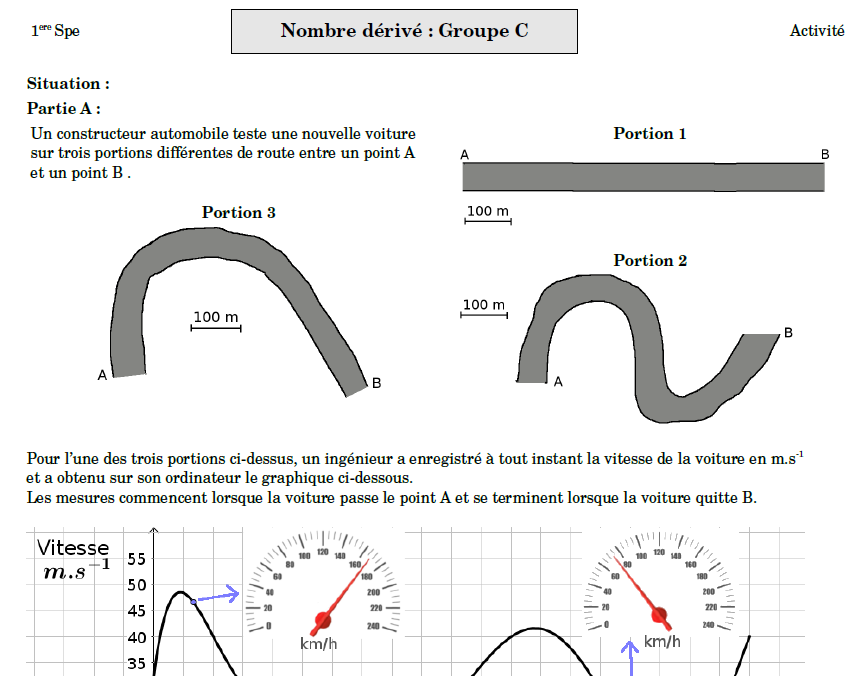--- ### Nombre dérivé en spé maths #### Exemple 2 - Excès de vitesse 💡idée : introduire le nombre dérivé comme une vitesse instantannée dans un situation familière. Vitesses en km/h. Référence : https://pia.ac-paris.fr/portail/jcms/p1_683257/exces-de-vitesse-ou-pas-lycee-1re ---- #### Exemple 2 - Excès de vitesse | Document élève | énoncé | | -------- | -------- | | <img src="https://minio.apps.education.fr/codimd-prod/uploads/96c2186ec322d4d78a95d169b.png" width="2000pt"> | On roule 4h en voiture sur autoroute. Les gendarmes nous arrêtent en fin de parcours et nous accusent d'avoir fait un excès de vitesse. Est-ce possible ? 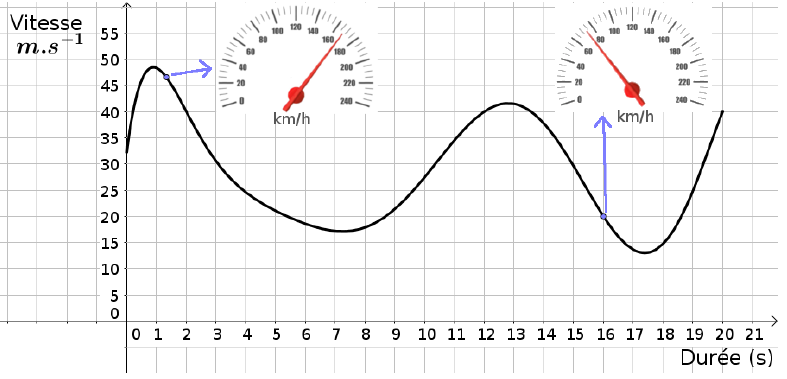| ---- #### Exemple 2 - Excès de vitesse **Scénario :** * On laisse les élèves chercher avec le graphique. * Au tableau, on effectue plusieurs calculs de vitesses moyennes en utilisant la notation $\frac{\Delta y}{\Delta x}$ puis $\frac{f(a+h)-f(a)}{h}$ * Manipulation d'un fichier GeoGebra : Zoom sur la courbe, sécantes mobiles, introduction de la tangente. 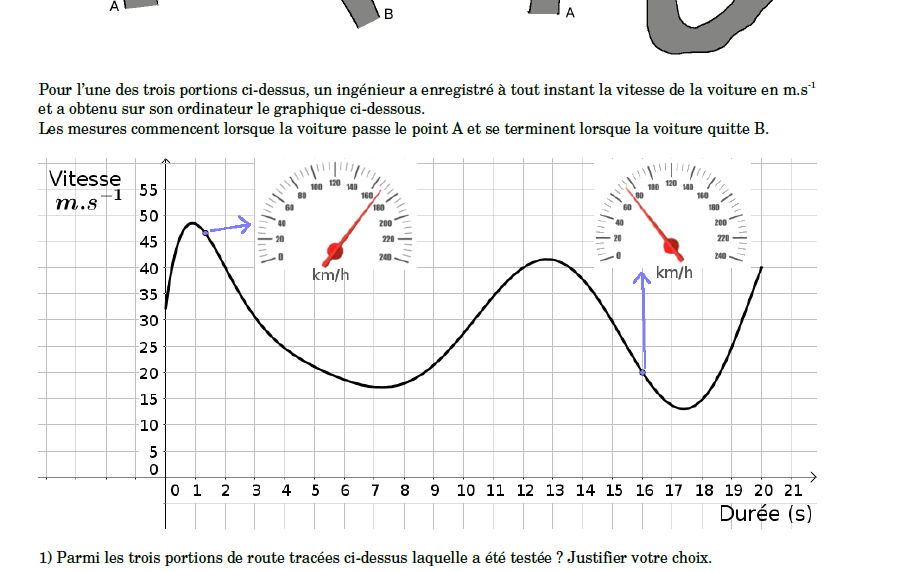---- #### Exemple 2 - Excès de vitesse Variantes et questions subsidiaires : * utiliser une courbe moins régulière. * Q : où pouvait se trouver un radar ? * Q : quelle a été la vitesse maximale ? --- ### 🧩 Jigsaw  Méthode *Jigsaw* dans le document académique "[L'Oral en mathématiques](https://pedagogie.ac-orleans-tours.fr/spip.php?article1688)", rubrique *Se Former*. 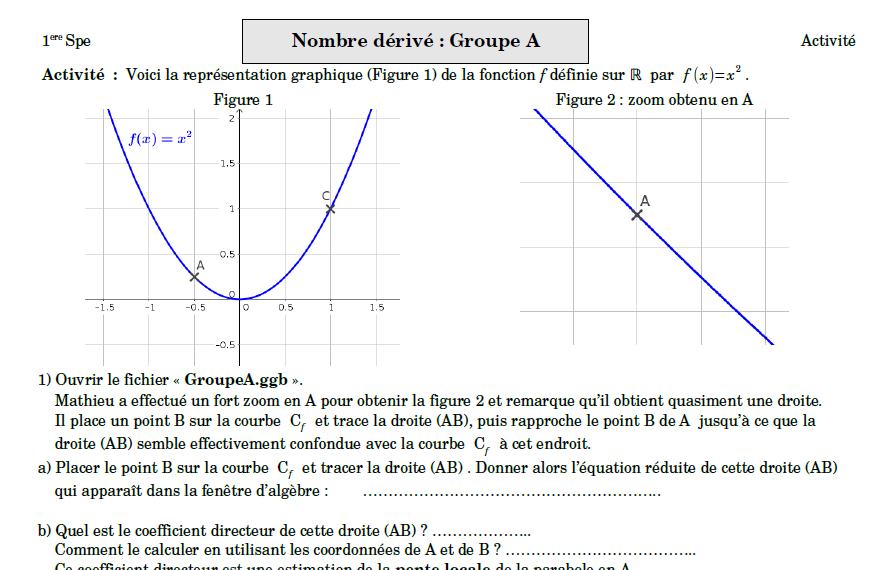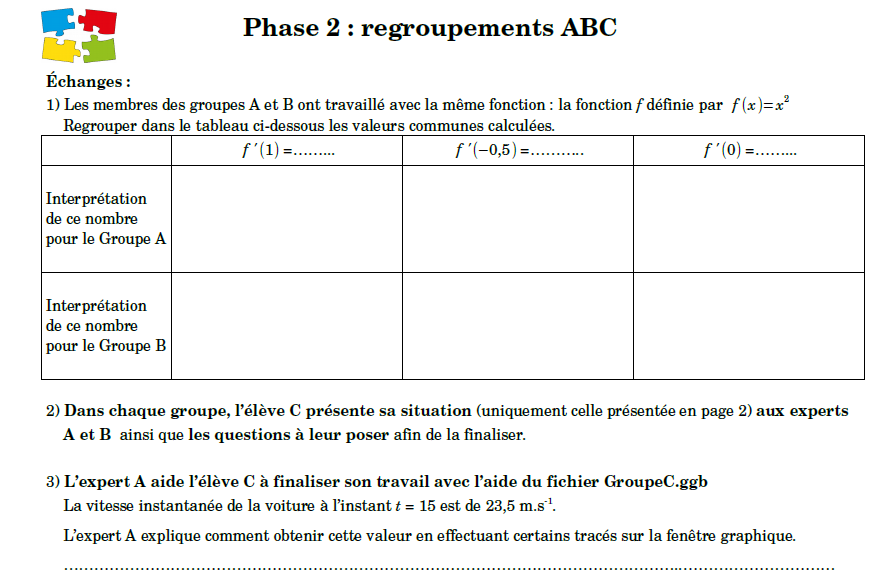---- ### 🧩 Jigsaw 1. Trois groupes A, B, C ont des documents avec des approches différentes : A : Zoom B : Taux de variation C : Vitesse instantanée 3. Regroupement pour une tâche commune [pedagogie.ac-rennes.fr/spip.php?article4598](https://pedagogie.ac-rennes.fr/spip.php?article4598) <!--https://jigsawirem.wixsite.com/jigsaw-mathematiques--> ----  ----  ----  ---- <!-- -->  ---- <img src="https://minio.apps.education.fr/codimd-prod/uploads/cfd629a2a56fbb4614f5b2261.png" width="80%"> ----  ---- #### Autre 🧩 Jigsaw possible Nicolas Rency en STMG. **Phase 1** (experts - différenciation) * A : lecture de coefficients directeurs * B : taux de variation entre 2 valeurs * C : découverte de la limite **Phase 2** (tâche commune) Livret GeoGebra sur la croissance d'un enfant. --- ## Bilan * En amont : retravailler la notion de coefficient directeur, de taux de variation (automatismes). * Manipulation (pliage, tracés, numérique,...) * Utiliser des graphiques représentant des grandeurs pour donner un sens et une unité au coefficient directeur des sécantes et tangentes. * Outils numériques : GGB, calcul formel, tableur * Différents registres : graphiques, calcul, tableaux de valeur. --- <!-- .slide: data-background="https://minio.apps.education.fr/codimd-prod/uploads/96c2186ec322d4d78a95d16c5.png"--> ### <i class="fa fa-exclamation-triangle" aria-hidden="true" style="color: rgb(245, 197, 66);"></i> Conceptions erronées. 1. "La tangente est la droite qui coupe la courbe en un seul point." 2. "Non, OK, mais au moins sur un intervalle autour de ce point" 3. $f'(a)>0$ signifie que $f$ est croissante au voisinage de $a$. ---- ### <i class="fa fa-exclamation-triangle" aria-hidden="true" style="color: rgb(245, 197, 66);"></i> Conceptions erronées. 1. "La tangente est la droite qui coupe la courbe en un seul point." ❌ <img src="https://minio.apps.education.fr/codimd-prod/uploads/96c2186ec322d4d78a95d16aa.png" "width=40%"> ---- ### <i class="fa fa-exclamation-triangle" aria-hidden="true" style="color: rgb(245, 197, 66);"></i> Conceptions erronées. 2. "La tangente en un point est la droite qui coupe la courbe uniquement en ce point au moins sur un voisinage de ce point." ❌ <img src="https://minio.apps.education.fr/codimd-prod/uploads/96c2186ec322d4d78a95d16b9.png" "width=70%"> ---- ### <i class="fa fa-exclamation-triangle" aria-hidden="true" style="color: rgb(245, 197, 66);"></i> Conceptions erronées. 3. $f'(a)>0$ signifie que $f$ est croissante au voisinage de $a$.❌ <img src="https://minio.apps.education.fr/codimd-prod/uploads/96c2186ec322d4d78a95d16bb.png" "width=70%"> --- ### Equation de la tangente * 💡 Est-il nécessaire de faire apprendre la formule ? * 💡 Travailler en 2de des équations réduites de droite connaissant le coefficient directeur $m$ et un point $A(x_A ; y_A)$. $y=m(x-x_A)+y_A$ --- ## Place aux échanges  <style> /* Ne pas effacer ce qui est ci-dessous. C'est du code CSS pour définr le style du diaporama */ /* Utiliser la police Marianne */ .reveal { font-family: 'Marianne', font-size: 2.5em; } /* Aligner le texte à gauche */ .reveal p, .reveal h1, .reveal h2, .reveal h3, .reveal h4, .reveal h5, .reveal h6 { text-align: left; } /* Aligner les listes à puce à gauche avec une marge de 15px */ .reveal ul { list-style-position: outside; margin-left: 10px; } /* Aligner les titres de diapositives à gauche */ .reveal .slides section { text-align: left; margin-top: 30px; } /* Numéro de diapositive en bas à gauche avec le titre du diaporama */ .reveal .slide-number { position: fixed; bottom: 10px; left: 15px; color: #888; /* Couleur grise */ font-size: 0.5em; background: none; /* Pas de fond */ z-index: 1000; } /* Barre de progression plus épaisse en rouge avec fond gris */ .reveal .progress { height: 8px; /* Hauteur de la barre */ background: #ccc; /* Fond gris */ } .reveal .progress span { background: #ff0000; /* Couleur rouge */ } /* Changer la couleur de survol des liens */ .reveal a:hover { color: #ff0000; /* Couleur rouge lors du survol */ } /* Ajouter une bordure grise très fine autour des images */ .reveal .slides img { border: 1px solid #ccc; /* Bordure grise de 1 pixel */ /* box-shadow: none; /*Supprimer l'ombre (si elle est appliquée) */ } </style>