---
tags: fourier, fft, tdf ,transformé
title: tfd version élève
---
# Transformée de Fourier Discrète
https://tinyurl.com/transf-fourier-discrete
## I. Approximation de fonction continue
### 1.par des polynômes
$$e^x=1+x+x^2/3+x^3/6+...$$
### 2.par des fonctions trigonométriques 
$0,19sin(πx)+0.086sin(3πx)+0.044sin(5πx)–0.035sin(7πx)+0.038sin(9πx)+...$
$+0.005sin(11πx)–0.004sin(13πx)+0.007sin(15πx)+0.004sin(17πx)+0.008sin(19πx)+..$
## II. La transformée de Fourier 
Voici une métaphore simple:
- Que fait la transformée de Fourier ? A partir d'un smoothie, elle trouve sa recette.
- Comment ? Elle passe le smoothie dans un filtre pour en extraire chaque ingrédient.
- Pourquoi ? Les recettes sont plus faciles à analyser, comparer et modifier que le smoothie lui-même.
- Comment récupérer le smoothie ? Re-mélanger les ingrédients.

**l'idée**: il est plus simple de connaitre les fréquences et leur amplitudes (partie droite ) que toutes les valeurs de la fonction (son ici, partie gauche)
## III. La Transformée de Fourier Discrète 
:::warning
Soient $x_0,x_1,...,x_{N-1}$ , N valeurs d'un signal discret $x.
On a $X$ la Transformée de Fourier de Discrète de $x$ tel que
Pour $k = 0, 1, \dots, N-1 \quad$,$$\quad X[k] = \sum_{n=0}^{N-1} x[n] e^{-j \frac{2\pi}{N} kn}$$
En posant $\omega=e^{-j \frac{2\pi}{N}}$, on a $$\quad X[k] = \sum_{n=0}^{N-1} x[n] \omega^ {kn}$$
:::
Rq: $\omega$ est la racine primitive $N$-ième de l'unité :
$\quad X[0] = \sum_{n=0}^{N-1} x[n] \omega^ {0n}= \sum_{n=0}^{N-1} x[n]=x_0+x_1+x_2\dots+x_n$
$\quad X[1] = \sum_{n=0}^{N-1} x[n] \omega^ {1n}= \sum_{n=0}^{N-1} x[n]\omega^n=x_0+x_1\omega+x_2\omega^2\dots+x_n\omega^{N-1}$
$\quad X[2] = \sum_{n=0}^{N-1} x[n] \omega^ {2n}= \sum_{n=0}^{N-1} x[n](\omega^2)^n=x_0+x_1\omega^2+x_2\omega^4\dots+x_n(\omega^2)^{N-1}$
La Transformée de Fourier Discrète (DFT) d'un vecteur $\mathbf{x}$ de longueur $N$ peut être exprimée sous forme matricielle :
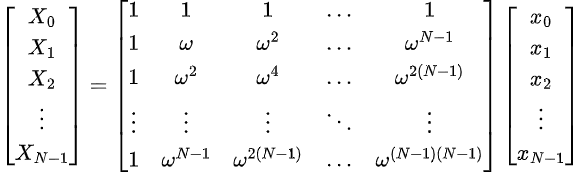
$$X=W_n\times x$$
où :
- $\mathbf{X}$ est le vecteur des coefficients de la DFT.
- $\mathbf{x}$ est le vecteur des échantillons du signal.
- $W_n$ la matrice carrée (de Vandermonde)
$W_2 = \begin{bmatrix}
1 & 1 \\
1 & e^{-i \frac{2\pi}{2}} \\
\end{bmatrix}
= \begin{bmatrix}
1 & 1 \\
1 & -1 \\
\end{bmatrix}$,$W_4=\begin{bmatrix}
1 & 1 & 1 & 1 \\
1 & i & -1 & -i \\
1 & -1 & 1 & -1 \\
1 & -i & -1 & i \\
\end{bmatrix}$
---
- **TFD inverse :** $x=W_n^{-1}\times X$ , avec $W_n^{-1}$ facile à déterminer
$$\quad x[k] = \sum_{n=0}^{N-1} X[n] e^{+j \frac{2\pi}{N} kn}$$
#### Exemple 1
Pour n = 3, on considère $x_0 = 0, x_1 = 1$ et $x_2 = 2$(par exemple)
La TFD de la séquence $(x_0, x_1, x_2)$ est la séquence $(X_0, X_1, X_2)$ avec :
• $X[0] = \sum_{n=0}^{3-1} x[n] \omega^ {0n}= \sum_{n=0}^{2} x[n]=x_0+x_1+x_2= 0 + 1 + 2 = 3$
• $X[1] =\dots$
• $X[2] =\dots$
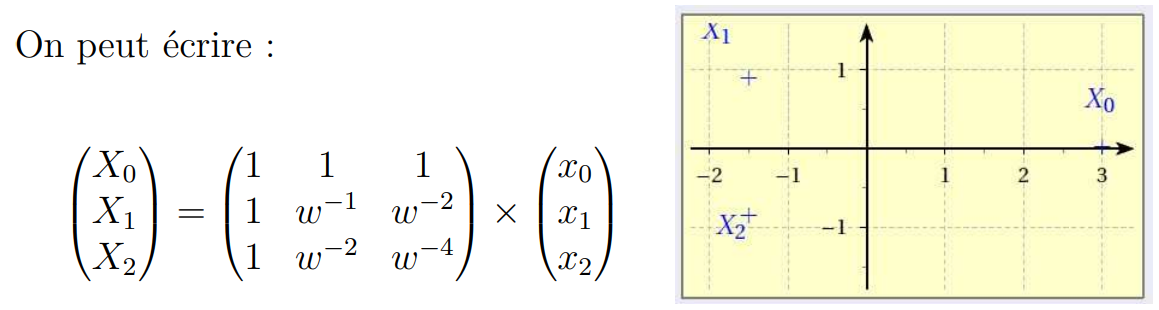
## IV.Transformée de Fourier Rapide (Cooley -Tukey)
Il existe une façon de calculer la TFD beaucoup plus rapidement, c'est l'algorithme de Transformée de Fourier Rapide (sigle anglais : FFT ou fast Fourier transform). C’est celui utilisé par tous les logiciels de traitement du signal.
En effet la multiplication de matrices demande $n^2$ multiplications.

**Il se base sur une approche de type ***« diviser pour régner »*** par le biais d'une récursion.**
**Exemple 1: n=4**


## V.Applications
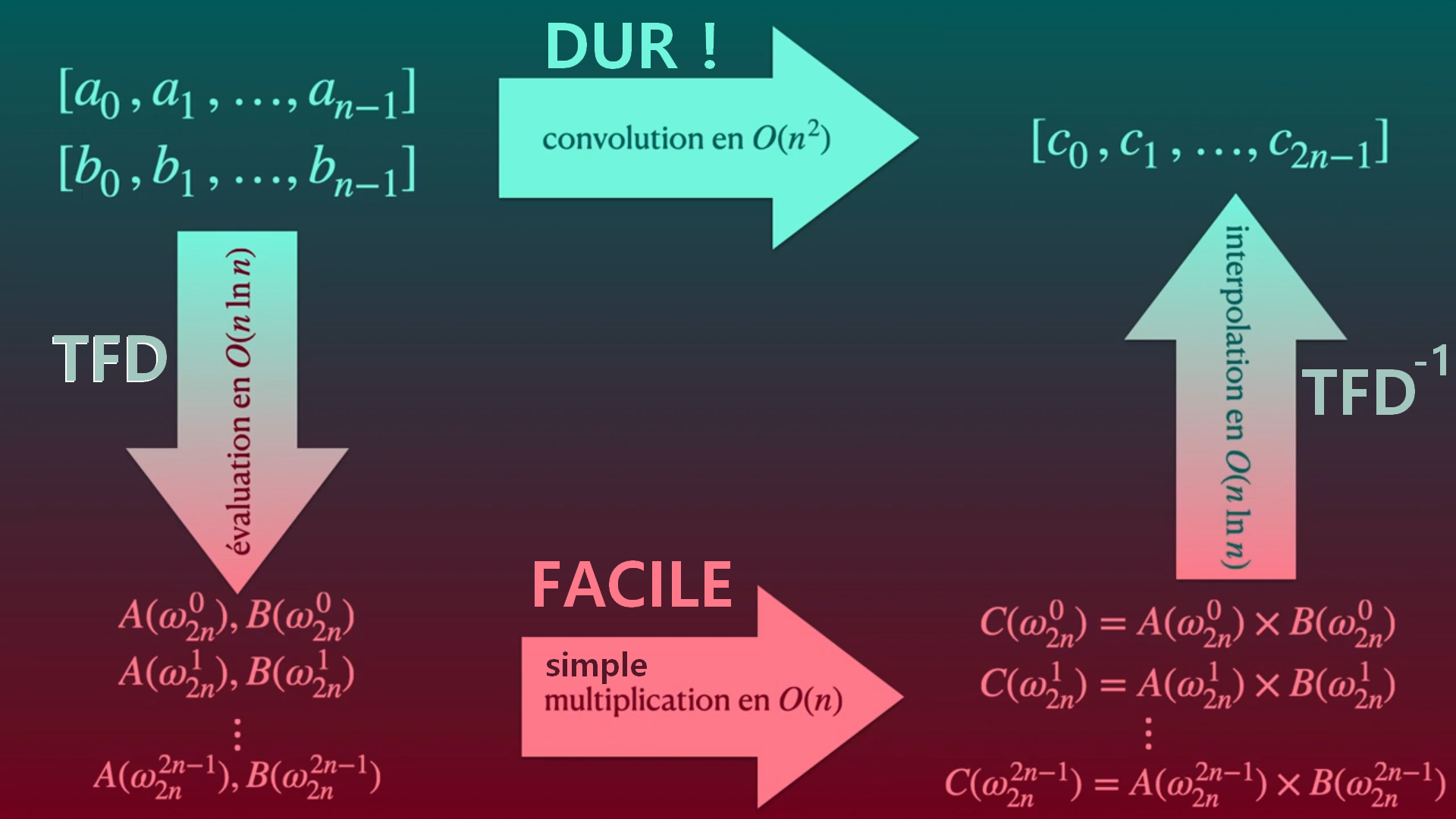
### 1.Polynômes et FFT
LA TFD transforme la convolution en simple produit.
https://capytale2.ac-paris.fr/web/c/844d-5541312
### 2.(épi)ⁿ-cycloïdes
:::warning
**Soleil,Terre,Lune**
elles tourne, tournent, tournent...
:::
:::warning
Avec Geogebra $$3 ℯ^{i α}+2 ℯ^{i 2α}$$
:::
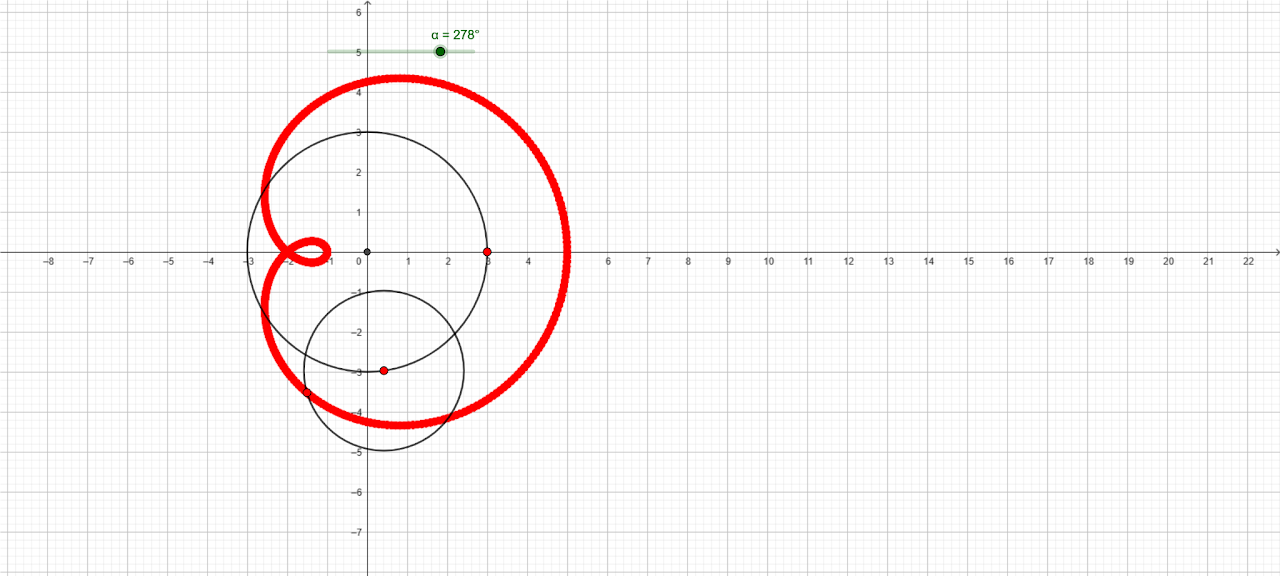[anim](https://www.geogebra.org/classic/er8kqwpj)
Une excellente question à se poser, c'est celle de l'équation des courbes que l'on obtient.
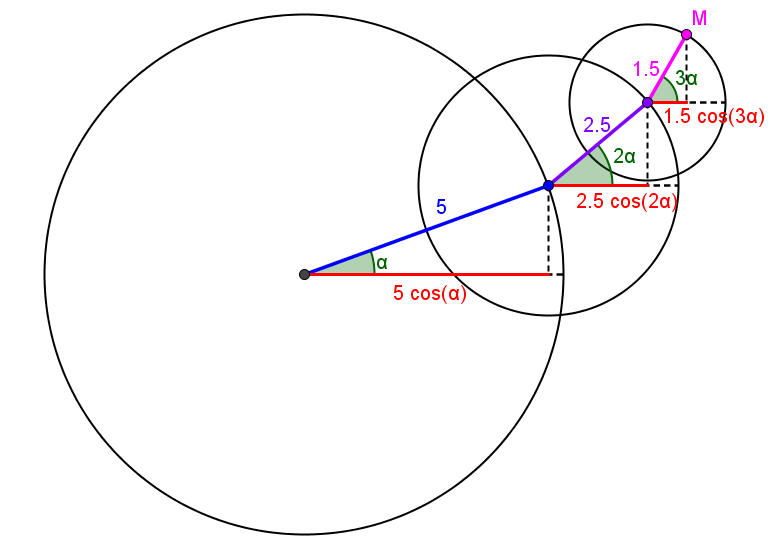
Le point M a pour affixe:
$$z=5e^{i\alpha}+2,5e^{i3\alpha}+1,5e^{i3\alpha}$$
:::warning
Dessiner un éléphant avec des cercles !
:::
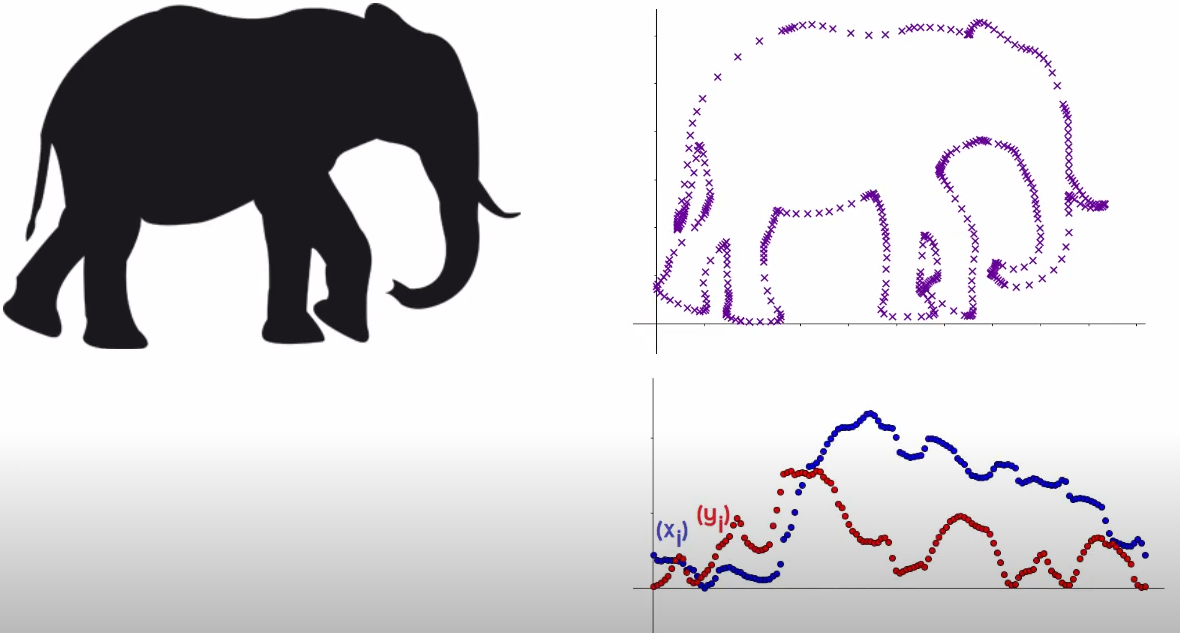
Figure à main levée (continue, périodique,pas d'équation math)
On discrètise pour avoir un nombre fini de points $(x_n,y_n)$ avec $n=0...N-1$
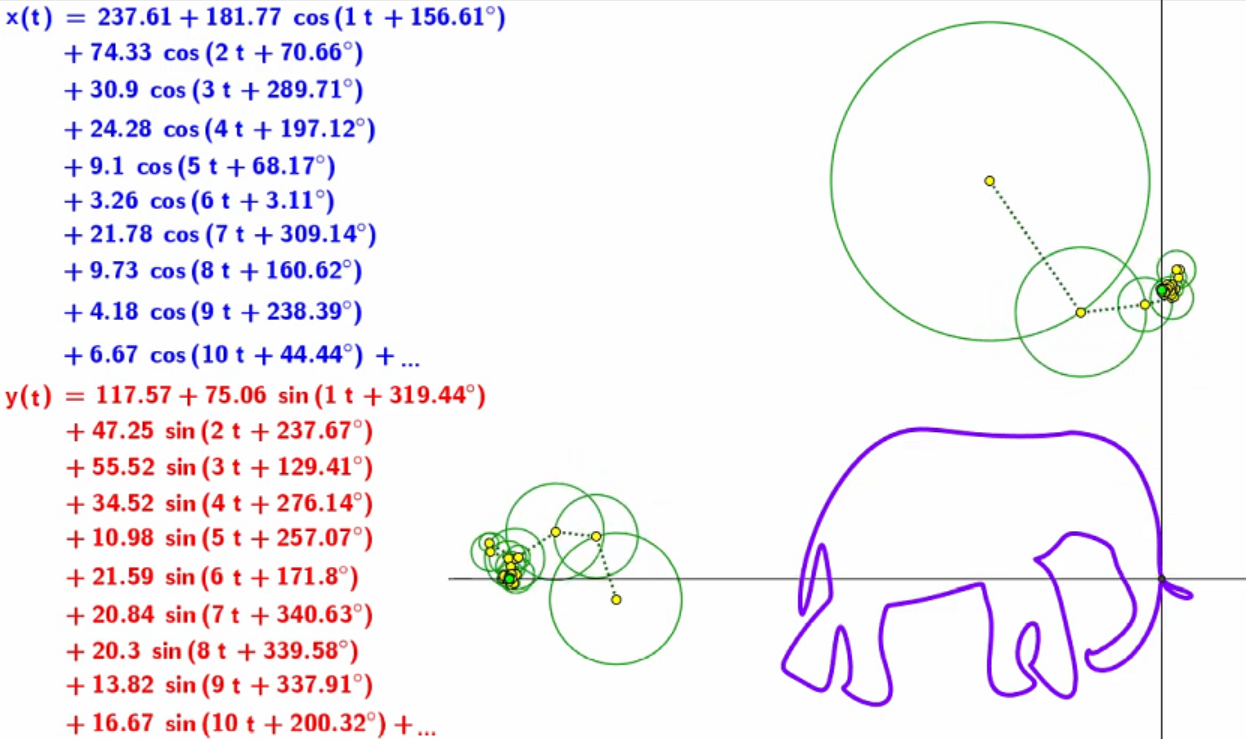
On calcule les TFD X et Y:
- $$\quad X[k] = \sum_{n=0}^{N-1} x[n] e^{-j \frac{2\pi}{N} kn}$$
- $$\quad Y[k] = \sum_{n=0}^{N-1} y[n] e^{-j \frac{2\pi}{N} kn}$$
Puis la TFD inverse permet d'avoir :
- $$\quad x[k] = \sum_{n=0}^{N-1} X[n] e^{+j \frac{2\pi}{N} kn}$$
- $$\quad y[k] = \sum_{n=0}^{N-1} Y[n] e^{+j \frac{2\pi}{N} kn}$$
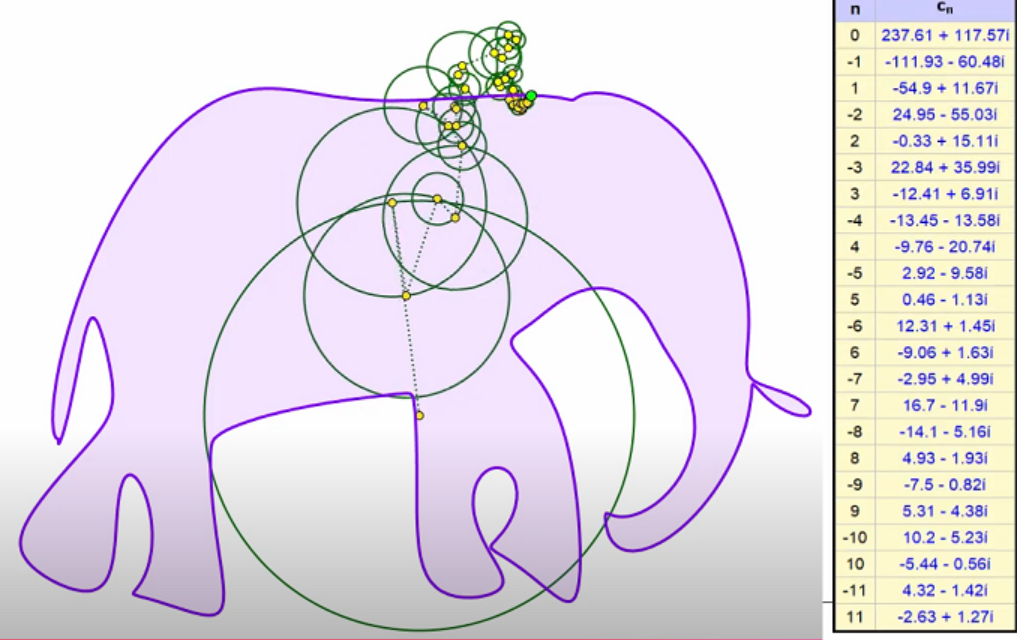
Rq: si on considère les points $(x_n,y_n)$ comme des nombres complexes $y_n=x_n+iy_n$,on peut alors calculer Z, la TDF de x:
$$\quad Z[k] = \sum_{n=0}^{N-1} z[n] e^{-j \frac{2\pi}{N} kn}$$
Puis la TFD inverse permet d'avoir :
- $$\quad z[k] = \sum_{n=0}^{N-1} Z[n] e^{+j \frac{2\pi}{N} kn}$$
<style>
h1{text-align: center;color: white; background-image: linear-gradient(to right , #ffca08, #DBAF0D) ;border-radius: 10px;}
h2{ color:#0070C0}
</style>