# Les congruences --- L'idée de traiter de nombres avec les restes de leur division par certains entiers au lieu de traiter avec ces nombres eux-mêmes a fait son chemin au fil des temps. Gauss l'a structurée avec ses « congruences », qui ont donné le jour à l'arithmétique modulaire d'aujourd'hui. Les congruences, toute une histoire ! --- Du « théorème des restes chinois », hérité de la Chine antique et étudié jusqu'au XIIIe siècle, à celui de Fermat, le domaine connaîtra de nombreux progrès, jusqu'à l'arrivée de Gauss, qui formalisera la notion de « congruence » et signera l'acte de naissance de l'arithmétique modulaire. --- Cette nouvelle et puissante vision des nombres, qui permet d'englober l'infinité des entiers dans un modèle fini, s'applique aussi à des domaines concrets : la preuve par 9, les cycles des calendriers, les codes de sécurité... --- Elle se retrouve aussi en musique et produit quelques jolies curiosités, comme certains tours de magie. ---  --- En 1801, dans ses Disquisitiones arithmeticae (« Réflexions arithmétiques »), au texte entièrement en latin, le mathématicien allemand Carl Friedrich Gauss introduit explicitement les congruences : il s’agit désormais de ne plus étudier les nombres isolément, mais en leur attachant tous ceux qui ont même reste qu’eux dans la division par un certain nombre. Même si une telle approche de l’arithmétique remonte à l’Antiquité, l’ouvrage de Gauss fera date dans l’histoire de la théorie des nombres. --- ## Compter comme une horloge On a tous usé des congruences sans le savoir, ne serait-ce qu’en faisant, dès l’école primaire, la preuve par 9 d’une multiplication. --- Pour vérifier, par exemple, que 47 × 19 est bien égal, comme on vient de le calculer, à 893, on compare le produit des restes de 47 et de 19 dans la division par 9, c’est-à-dire 2 × 1, au reste du résultat, ici 2. S’il y a égalité, le résultat a de grandes chances d’être exact. Sinon, il est certain que le résultat est faux. --- On sait aussi depuis notre enfance que, sur le cadran d’une horloge, « 14 h » se lit "deux heures". Ainsi, sur une horloge, 14 veut dire la même chose que 2. Cela veut-il dire que 14 = 2? Dans un certain sens, peut-être que oui… --- Dans notre exemple, les nombres 14 et 2 peuvent être considérés comme des « égaux de l’horloge ». Les mathématiciens et mathématiciennes ont une façon particulière d’exprimer cette réalité. Ils disent que ces nombres sont des congrus modulo 12 si leur différence est de 12, 24, 36 ou n’importe quel autre multiple de 12. --- Les nombres 2 et 14 en sont un exemple. Sur une horloge, ils signifient la même chose. 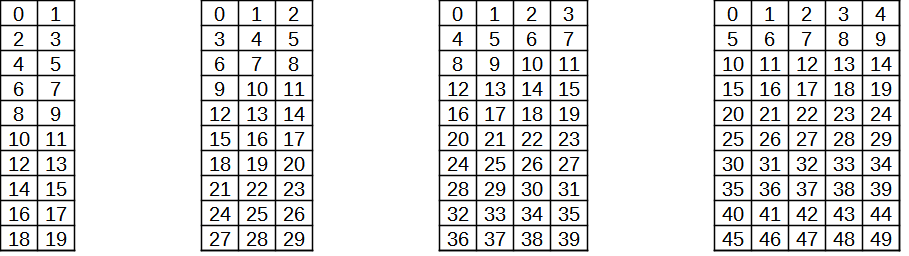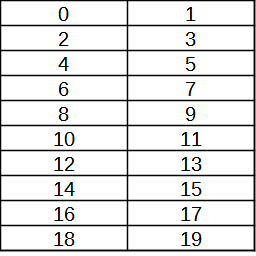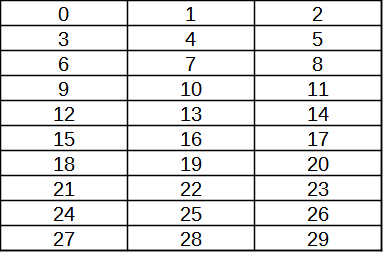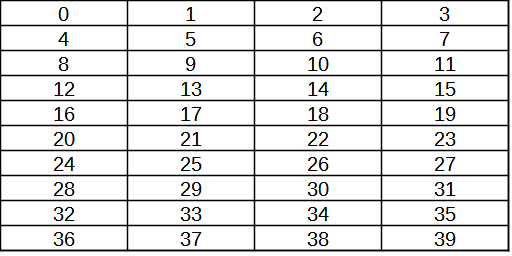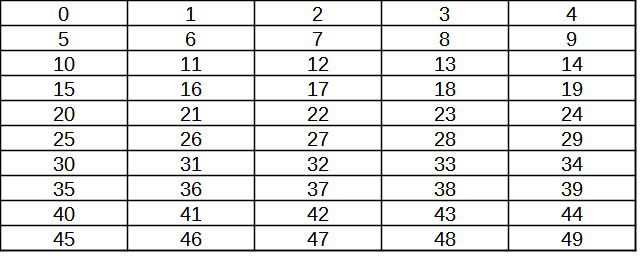Mathématiquement, cela s’exprime de la manière suivante : $$2 \equiv 14 \mod {12}$$ 2 et 14 sont des nombres congrus en modulo 12 --- On écrit les entiers par rangées de 2, de 3, de 4, ... dans différents tableaux, comme ci-dessous.  --- - Justifier que les nombres contenus dans la première colonne sont tous divisible par le nombre de colonnes. - Justifier que les nombres dans la 2e colonne ont tous pour reste 1 dans la division par le nombre de colonnes du tableau. Qu'en est-il pour les autres colonnes ? - Soit n le nombre de colonnes du tableau. Décrire les nombres contenus dans la colonne qui commence par le nombre p ---  ---  ---  ---