<style> mark{ background: yellow; font-weight: bold; } // https://lucidar.me/fr/web-dev/css-color-list/ </style> # DNB Juin 2025 Centres étrangers Groupe 1 : une correction du sujet de mathématiques > *Conçu à partir d'un [sujet original scanné](http://college.valdugy.free.fr/IMG/pdf/dnb_juin2025_centreetrangersg1.pdf).* > *Merci aux relecteurs Laly, Baptiste, Timothée, Zoé, Cassandra, Maëlys, Kassandra, Chloé, Cybèle et Katie.* > (c) CC by-Nc - 18 juin 2025 - Keops ([E.Ostenne](mailto:emmanuel.ostenne@ac-lille.fr?subject=CodiDNBjuin2025)) # Exercice 1 (20 points) Cet exercice est un questionnaire à choix multiple (QCM). Pour chaque question, quatre réponses sont proposées. ++**Une seule réponse est exacte.**++ **Recopier sur la copie** le numéro de la question **et** la réponse choisie. Aucune justification n’est demandée. ## Question 1 La décomposition en produit de facteurs premiers de 120 est : | Réponse A | Réponse B | Réponse C | Réponse D | |:---------:|:---------:|:---------:|:--------- | | 2x3x4x5 | 15x2x2x2 | 2^3^x3x5 | 53 + 67 | :::success ::: spoiler ++Correction++ <mark>1-C</mark> *La justification n'était pas demandée.* La réponse D n'est pas une décomposition en facteurs premiers : il n'y a pas de multiplication. Pour les réponses A et B la décomposition en facteurs comporte des nombres qui ne sont pas premiers : 4 et 15. Donc il ne reste que la proposition C (et elle comporte bien des nombres premiers multipliés). ::: ## Question 2 Dans la cellule A2, la formule « = -4*A1-12 » a été saisie. | | A | B | |:-----:|:---:|:---:| | **1** | 2 | 5 | | **2** | -20 | | On l’étire jusqu’à la cellule B2. 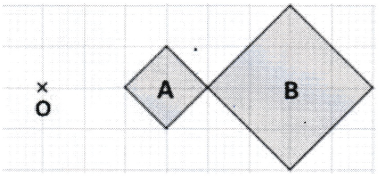La valeur obtenue dans la cellule B2 est : | Réponse A | Réponse B | Réponse C | Réponse D | |:---------:|:---------:|:---------:|:---------:| | -32 | -20 | 8 | 68 | :::success ::: spoiler ++Correction++ <mark>2-A</mark> *La justification n'était pas demandée.* On applique la formule en remplacçant A1 par B1 qui est à sa droite : -4*B1-12 donnera donc -4×5-12 = ++-32.++ ::: ## Question 3 Sur la figure ci-contre, le rapport de l’homothétie de centre O qui transforme le carré A en le carré B est :  | Réponse A | Réponse B | Réponse C | Réponse D | |:---------:|:---------:|:---------:|:---------:| | -2 | -0,5 | 0,5 | 2 | :::success ::: spoiler ++Correction++ <mark>3-D</mark> *La justification n'était pas demandée.* Le côté du carré A a pour longueur 1 diagonale du carreau de quadrillage et le côté du carré B a pour longueur 2 diagonales du carreau de quadrillage. Par une homothétie, la longueur du côté de l'image est obtenue en multipliant la longueur du côté par le rapport d'homothétie. Comme 2 = 1 × 2, le rapport d'homothétie est ++2++. ::: ## Question 4 Une écriture factorisée de $4 \times x^2 — 1$ est : | Réponse A | Réponse B | Réponse C | Réponse D | |:------------------ |:------------------:|:-----------------:|:------------:| | $(2x — 1)(2x + 1)$ | $(4x — 1)(4x + 1)$ | $4(x — 1)(x + 1)$ | $(2x — 1)^2$ | :::success ::: spoiler ++Correction++ <mark>4-A</mark> *La justification n'était pas demandée.* On reconnaît une identité remarquable de la forme a²-b² = (a-b)(a+b) avec a²=4x² et b²=1. 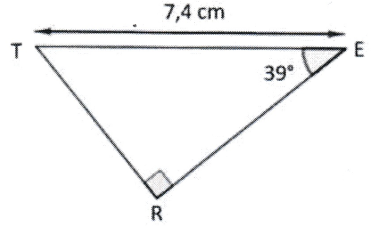On peut prendre a=2x et b=1 donc $4x^2 — 1=(2x — 1)(2x + 1)$ ::: ## Question 5 Dans le triangle TER ci-contre, la mesure de la longueur RE arrondie au centième de cm est :  | Réponse A | Réponse B | Réponse C | Réponse D | |:--------- |:---------:|:---------:|:---------:| | 4,66 cm | 5,75 cm | 9,52 cm | 11,76 cm | :::success ::: spoiler ++Correction++ <mark>5-B</mark> *La justification n'était pas demandée.* D'après le codage, le triangle TER est rectangle en R. Donc $cos(\widehat{TER}) = \dfrac{RE}{TE}$ d'où $cos(39°)=\dfrac{RE}{7,4}$ et $RE=7,4 \times cos(39°)$ soit $RE \approx 5,75$. ::: # Exercice 2 (19 points) L'entreprise « Transport Rapide » doit livrer cinq colis nommés A, B, C, D et E ayant des masses différentes précisées dans le tableau ci-dessous : | Nom du colis | A | B | C | D | E | |:------------:|:---:|:---:|:---:|:---:|:---:| | Masse en kg | 4 | 9 | 2 | 7 | 11 | 1. Calculer la moyenne des masses des colis en kg. :::success ::: spoiler ++Correction++ La somme des valeurs donne 4+9+2+7+11 = 33 Comme il y a 5 valeurs : 33/5 = 6,6 Donc la moyenne des masses est <mark>6,6 kg</mark>. ::: 2. Déterminer la médiane des masses des colis en kg. Interpréter ce résultat. :::success ::: spoiler ++Correction++ On range les masses des colis dans l'ordre croissant : 2; 4; ++7++; 9; 11 Comme 7 est au centre, la médiane est <mark>7 kg</mark>. Cela signifie que <mark>la moitié des colis pèse moins de 7 kg</mark>. ::: 3. Le transporteur choisit au hasard un colis parmi les cinq (A, B, C, D ou E) pour une livraison express. Calculer la probabilité pour qu’il sélectionne un colis dont la masse est inférieure à 8 kg. :::success ::: spoiler ++Correction++ Il y a 3 colis de moins de 8 kg parmi les 5 donc la probabilité se calcule par $\dfrac{3}{5}$ (ce qui fait 0,6 ou 60 %). <mark>$\dfrac{3}{5}$</mark> est la probabilité pour qu’il sélectionne un colis dont la masse est inférieure à 8 kg ::: Les colis ont la forme d'un pavé droit de longueur L, de largeur l et de hauteur h, représenté ci-dessous.  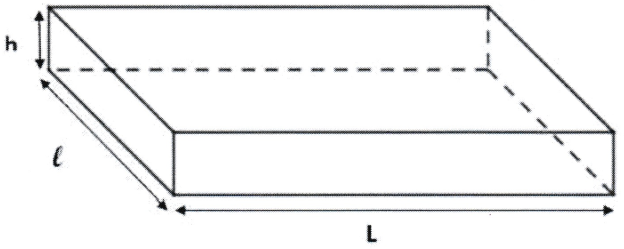Voici les dimensions des cinq colis. | Colis | Longueur L<br>en mètre | Largeur l<br>en mètre | Hauteur h<br>en mètre | |:-----:|:----------------------:|:---------------------:|:---------------------:| | A | 0,4 | 0,3 | 0,5 | | B | 0,5 | 0,4 | 0,8 | | C | 0,3 | 0,1 | 0,5 | | D | 0,4 | 0,3 | 0,7 | | E | 0,5 | 0,4 | 0,6 | 4. a. Vérifier que le volume du colis E est de 0,12 m^3^. :::success ::: spoiler ++Correction++ V=Lxlxh D'après les indications : V=0,5×0,4×0,6 <mark>V=0,12 m^3^</mark>. ::: b . L'entreprise souhaite calculer la masse volumique d’un colis dont la formule est rappelée ci-dessous. Montrer que la masse volumique du colis E arrondie au dixième est 91,7 kg/m^3^. | | | | | --- | ------------------------------------------------------------------------------------------------------------------------ | --- | | | On rappelle que la formule qui permet de calculer la masse volumique d’un objet en kg/m^3^ est : $\dfrac{masse}{volume}$ | | | | | | :::success ::: spoiler ++Correction++ Le colis E pèse 11 kg pour un volume de 0,12 m^3^ donc µ = $\dfrac{11}{0,12}$ soit µ ≈ <mark>91,7 kg/m^3^</mark>. ::: c. Le transporteur affirme « Le colis E est plus lourd que le colis C, donc la masse volumique du colis E est plus grande que celle du colis C. » A-t-il raison ? :::success ::: spoiler ++Correction++ Le colis C pèse 2 kg d'après le premier tableau. A l'aide du deuxième tableau on calcule son volume 0,015 m^3^ : V = 0,3x0,1x0,5 V = 0,015 Donc sa masse volumique est donnée par µ=$\dfrac{2}{0,015}$ ce qui fait environ 133,3 kg/m^3^. La masse volumique du colis E est 91,7 kg/m^3^ : 133,3>91,7 donc <mark>il a tort</mark>. ::: # Exercice 3 (21 points) On considère le programme de calcul suivant. >- Choisir un nombre >- Multiplier le nombre choisi par —2 >- Ajouter 4 au résultat >- Multiplier le résultat obtenu par 4 1. Montrer que si l’on choisit 1 comme nombre de départ dans le programme, le résultat obtenu est 8. :::success ::: spoiler ++Correction++ - 1 - 1x(-2) = -2 - -2+4 = 2 - 2×4 = <mark>8</mark> ::: 2. Quel est le résultat si le nombre de départ est —2 ? :::success ::: spoiler ++Correction++ - -2 - -2×(-2) = 4 - 4+4 = 8 - 8×4 = 32 Le résultat est <mark>32</mark>. ::: 3. Si l’on note $x$ le nombre de départ, montrer que le résultat peut s’écrire $—8x + 16$. :::success ::: spoiler ++Correction++ - x - x×(-2) = -2x - -2x+4 - 4×(-2x+4) = 4×(-2)+4×4 = <mark>-8x+16</mark> ::: 4. a. Résoudre l’équation $—8x + 16 = 4$. :::success ::: spoiler ++Correction++ -8x+16=4 *on soustrait 16 aux 2 membres* -8x=-12 *on divise par -8 les 2 membres* x=$\dfrac{-12}{-8}$ soit x=$\dfrac{3}{2}$ La solution est $\dfrac{3}{2}$ ou <mark>1,5</mark>. ::: b. En déduire le nombre de départ qu’il faut choisir pour obtenir 4 comme résultat. :::success ::: spoiler ++Correction++ Pour obtenir 4 il faut que -8x+16 fasse 4. D'après a. <mark>ce nombre de départ est 1,5</mark>. 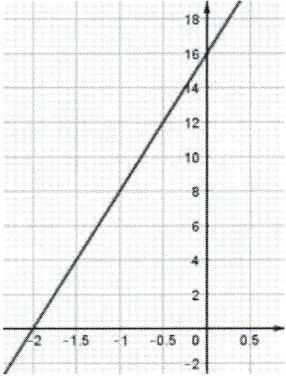::: 5. Parmi les trois représentations graphiques ci-dessous, quelle est celle qui représente la fonction $f$ définie par $f(x) = —8x + 16$ ? Expliquer la démarche. | Représentation<br>graphique 1 | Représentation<br>graphique 2 | Représentation<br>graphique 3 | |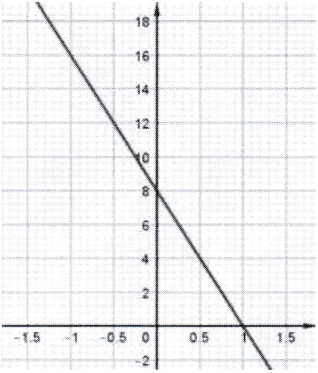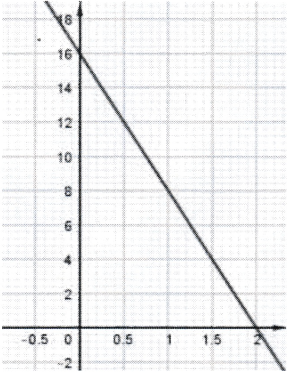:--------------------------------------------------------------------------------------:|:--------------------------:|:--------------------------:| |  |  |  | :::success ::: spoiler ++Correction++ $f(x) = —8x + 16$. - $f(0) = —8 \times 0 + 16 = 16$. La représentation graphique de $f$ passe donc par le point (0;16). Seules les représentations 1 et 3 peuvent convenir. - $f(1) = —8 \times 1 + 16 = 8$. La représentation graphique de $f$ passe donc par le point (1;8), ce qui correspond à la représentation 3 et non à la représentation 1. <mark>La représentation 3</mark> est la représentation graphqiue de la fonction $f$. *++Alternative :++* - -8 est le coefficient directeur de la fonction. Comme il est négatif, la droite va descendre de la gauche vers la droite sur le graphique : les représentations 2 et 3 pourraient convenir. - +16 est l'ordonnée à l'orgine. Donc la droite va passer par le point (0;16), ce qui correspond à **++la représentation 3++** et non à la représentation 2. ::: # Exercice 4 (21 points) Un agriculteur souhaite cultiver un champ représenté par le triangle ABC ci-dessous.  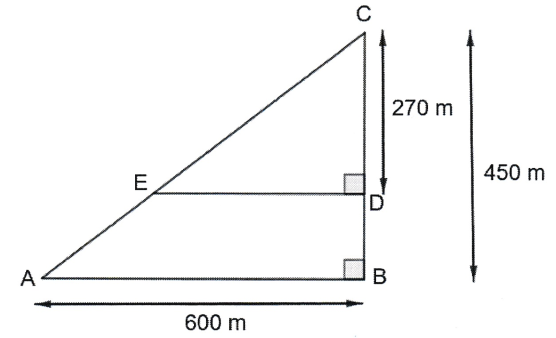Sur la figure qui n’est pas à l'échelle, on a les informations suivantes : - le triangle ABC est rectangle en B; - les points C, E et A sont alignés; - les points C, D et B sont alignés; - AB = 600 m; BC = 450 m; CD = 270 m. *Les parties A et B sont indépendantes.* ## Partie A : étude géométrique du terrain 1. Montrer que le segment [AC] mesure 750 mètres. :::success ::: spoiler ++Correction++ Le triangle ABC est rectangle en B, donc d'après la propriété de Pythagore, AC^2^ = AB^2^ + BC^2^. Donc AC^2^ = 600^2^ + 450^2^ AC^2^ = 52 600 AC = $\sqrt{52 600}$ <mark>AC = 750 m</mark>. ::: 2. a. Montrer que les droites (ED) et (AB) sont parallèles. :::success ::: spoiler ++Correction++ D'après les codages, les droites (ED) et (AB) sont perpendiculaires à la même droite (CB) donc <mark>elles sont parallèles</mark>. ::: b. Montrer que le segment [DE] mesure 360 mètres. :::success ::: spoiler ++Correction++ On reconnaît une configuration de Thalés. Les droites (AE) et (DB) se coupent en C et (ED)//(AB) donc d'après la propriété de Thalès, $\dfrac{CE}{CA} = \dfrac{CD}{CB} = \dfrac{ED}{AB}$ et $\dfrac{CE}{CA} = \dfrac{270}{450} = \dfrac{ED}{600}$ $\dfrac{270}{450} = \dfrac{ED}{600}$ donc $ED=\dfrac{270 \times 600}{450}$ donc <mark>DE = 360 m</mark>. ::: c. Montrer que l’aire du triangle CDE est 48 600 m^2^. :::success ::: spoiler ++Correction++ Aire($triangle$)=$\dfrac{base \times hauteur}{2}$ Aire(CDE) = $\dfrac{CD \times ED}{2}$ Aire(CDE) =$\dfrac{270 \times 360}{2}$ <mark>Aire(CE) = 48 600 m^2^</mark>. ::: ## Partie B : étude du prix du mélange de graines L’agriculteur souhaite semer un mélange de graines (blé, seigle et pois) en respectant les indications suivantes. | Indication 1 : prix au kilo pour chaque type de graine | Indication 2 : répartition du type de graines pour une surface de 10 000 m^2^ | |:---------------------------------------------------------:|:-----------------------------------------------------------------------------:| | Blé : 1,40 €/kg<br>Seigle : 1,30 €/kg<br>Pois : 2,10 €/kg | Blé : 80 kg<br>Seigle : 60 kg<br>Pois : 250 kg | 1. Un vendeur lui propose des sacs contenant un mélange de blé, seigle, et pois selon le ratio 16 : 12 : 8. Montrer que la composition de ce sac ne respecte pas l’indication 2. :::success ::: spoiler ++Correction++ Le ratio 16 : 12 : 8 signifie que si on divise les différentes masses de graines, on doit trouver le même nombre. - blé : 80÷16 = 5 - seigle : 60÷12 = 5 - pois : 250÷8 ≈ 31,25 Comme on n'a pas obtenu le même nombre, la composition et le ratio ne sont pas proportionnels donc <mark>la composition ne respecte pas l'indication 2</mark>. ::: 2. L'agriculteur souhaite semer le mélange de graines sur la partie du champ représentée par le triangle CDE dont l’aire mesure 48 600 m^2^. Il a calculé qu’il doit prévoir 388,80 kg de blé pour respecter la répartition indiquée dans l’énoncé. Justifier le calcul de l’agricuiteur. :::success ::: spoiler ++Correction++ L'indication 2 dit que pour 10 000 m^2^ il faut 80 kg de blé donc pour 48 600 m^2^, il en faut *m* kg par proportionnalité : *m* = 48 600 × 10 000 / 80 <mark>*m* = 388,80 kg</mark>. ::: 3. L'agriculteur dispose d’un budget de 1 500 € pour semer le mélange de graines sur la totalité des 48 600 m^2^ de terrain. Il a calculé qu’il doit acheter 388,80 kg de blé, 291,6 kg de seigle et 243 kg de pois pour respecter la répartition indiquée dans l’énoncé. L'agriculteur dispose-t-il d’un budget suffisant ? :::success ::: spoiler ++Correction++ Grâce à l'indcation 1, on sait que l'achat lui coûtera 1 433,70 € : 388,8×1,40 +291,6×1,30 +243×2,10 = 1 433,7 1 433,7<1 500 donc <mark>son budget est suffisant</mark>. ::: # Exercice 5 (19 points) Un digicode commande l’ouverture de la porte d’entrée de la maison de la grand-mère de Léna. Léna a oublié le code. Elle sait qu’il est composé d’une lettre A, B, ou C, suivie d’un chiffre compris entre 0 et 9. 1. Proposer deux codes différents que Léna peut tester. :::success ::: spoiler ++Correction++ <mark>A0 et B5</mark> sont 2 codes que Léna peut tester conformément à la description de l'énoncé. ::: 2. Quelle est la probabilité que la grand-mère de Léna ait choisi la lettre C dans son code ? :::success ::: spoiler ++Correction++ C représente une possibilité parmi les 3 lettres A, B ou C donc <mark>la probabilité d'avoir choisi la lettre C est $\dfrac{1}{3}$</mark> (ou environ 0,3 ou environ 33 %). ::: 3. Montrer que la probabilité que la grand-mère de Léna ait choisi le chiffre 7 dans son code est $\dfrac{1}{10}$. :::success ::: spoiler ++Correction++ 7 est une possibilité parmi les 10 chiffres de 0 à 9, donc <mark>la probabilité d'avoir choisi le chiffre 7 est $\dfrac{1}{10}$</mark>. ::: 4. Léna se souvient que sa grand-mère, enseignante de mathématiques à la retraite, aime bien les nombres premiers. Quelle est la probabilité que le code choisi par sa grand-mère comporte un nombre premier ? :::success ::: spoiler ++Correction++ 2, 3, 5 et 7 sont les seuls nombres premiers entre 0 et 9. Il n'y a donc que 4 possibilités parmi les 10 chiffres. $\dfrac{4}{10}=\dfrac{2}{5}$ donc <mark>la probabilité d'avoir choisi un nombre premier est $\dfrac{2}{5}$</mark> (ou 0,4 ou 40 %). ::: 5. a. Léna décide de tester tous les codes possibles. Elle estime qu'il lui faut 5 secondes pour essayer un code. Réussira-t-elle à ouvrir la porte de la maison en moins de 3 minutes ? :::success ::: spoiler ++Correction++ Une fois la lettre choisie, elle a 10 chiffres à tester. Comme il y a 3 lettres, elle a 30 codes à tester car 3×10 = 30. Comme elle met 5 s par code : 5×30=150, elle mettra 150 s. 150÷60=2,5 : elle mettra 2,5 min. Et 2,5<3, donc <mark>oui, elle réussira à ouvrir en moins de 3 minutes</mark>. ::: b. Le format de ce code garantit-il la sécurité de la maison ? Comment pourrait-on améliorer ce système de code ? :::success ::: spoiler ++Correction++ Avec moins de 3 minutes pour trouver le code, une intrusion sera possible en moins de 3 minutes ce qui représente peu de temps pour réagir (appeler des secours par exemple). <mark>Pour améliorer le code, il faudrait augmenter le nombre de lettres</mark> en utilisant tout l'alphabet : 26×10=260 et 260×5=1 300 et 1 300 ÷ 60 ≈ 21,7 : il faudrait moins de 22 minutes pour trouver le code, mais c'est suffisant pour prévenir des secours : les intrus évieront cette maison car le risque de se faire prendre est important avant même d'être entré. ::: 6. Chaque fois qu’un utilisateur saisit un code, un programme lui annonce si le code est correct ou faux. Le programme utilisé est noté ci-dessous.  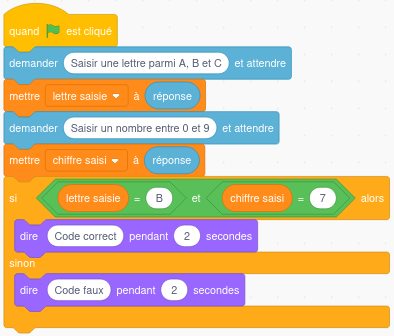a. Léna saisit le code B5. Qu’affiche le programme ? :::success ::: spoiler ++Correction++ Le bloc <span style=" background:darkorange;color:white;">[si]</span> teste si on a saisi le code B7 et répond "Code faux" si ce n'est pas B7. Donc <mark>le programme affiche "Code faux"</mark>. ::: b. D’après ce programme, quel est le code qui permet d’entrer dans l’immeuble de la grand-mère de Léna ? :::success ::: spoiler ++Correction++ Le bloc <span style=" background:darkorange;color:white;">[si]</span> teste si on a saisi le code B7 et répond "Code vrai" si c'est pas B7. Donc <mark>le code pour entrer est B7</mark>. :::