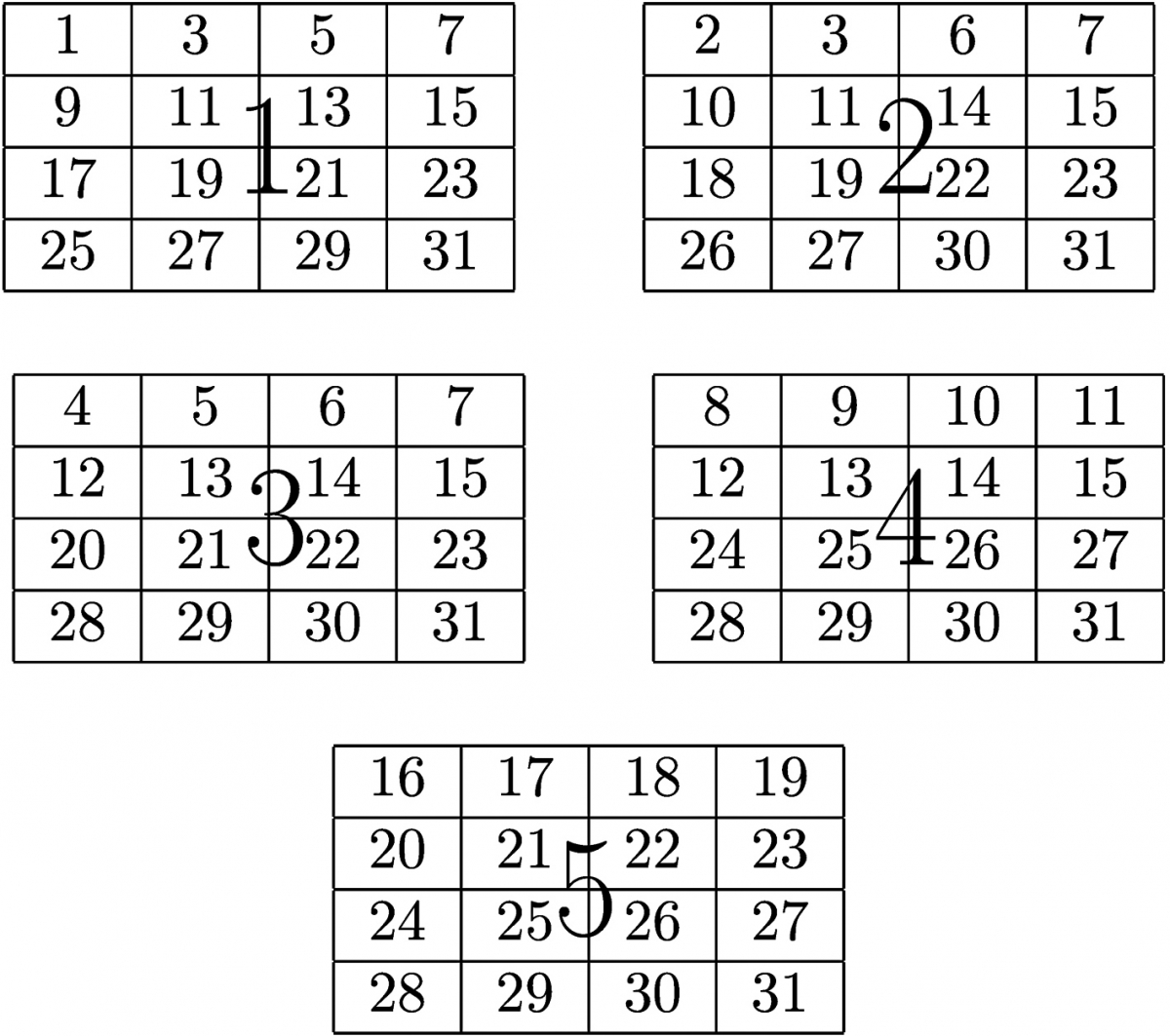
# BINAIRE ET ### CODAGE DES NOMBRES ET CARACTÈRES https://sites.google.com/view/sntqueneau/mais-aussi/information-binaire-hp  --- # 0 - intro: Magie [mon nombre](https://sorciersdesalem.math.cnrs.fr/Base2/base2.html) [mes cartes](https://codimd.apps.education.fr/p/hos16bfbA) --- <iframe width="100%" height="500" src="https://snap.berkeley.edu/snap/snap.html#present:Username=ChristianMercat&ProjectName=Magie1-31" > </iframe> --- :toprint:https://tinyurl.com/tourmagiebinaire  --- ## 1. Origine du binaire en informatique --- Dans les années 40, lorsqu'il a fallu passer de l'idée abstraite de machine de Turing (modèle mathématique) à la réalisation concrète du premier ordinateur (machine physique), la question des composants matériels à choisir s'est posée (transistor, lampe, DEL, aimant, tube, bande, …). Pour ces composants, il est possible de réduire leur fonctionnement à 2 états exclusifs l'un de l'autre : **état 0 et état 1.** --- - le transistor est bloqué (état 0) ou passant (état 1), - la lampe est éteinte (état 0) ou allumée (état 1), - le ruban est trouée (état 0) ou non (état 1), - la bande magnétique présente un pôle Nord (état 0) ou Sud (état 1). ---  Le langage de base finalement choisie pour l'informatique, et encore utilisé aujourd'hui, est **le binaire** dont l'unité est le **bit** : **bi**nary digi**t** (ou nombre binaire), pouvant prendre comme seules valeurs **0 ou 1**. L’**octet** (en anglais Byte) est une unité d'information composée de **8 bits**. L’octet est utilisé pour mesurer la capacité de stockage en mémoire ou sur un disque dur. 1 Byte = 1 octet = 8 bits --- **Exercice 1** Combien d'états différents peuvent être définis : avec 1 bit ? avec 2 bits ? avec 3 bits ? avec 4 bits ? avec 8 bits ? avec n bits ? --- # 2. Représentation binaire --- Un ordinateur réalise des calculs, il faut donc être capable de convertir tous nos nombres habituels écrit en base décimale, sous forme de mots binaires composés uniquement d'une suite de 0 et de 1, c'est-à-dire écrits en base deux. --- Pour nos nombres décimaux, le chiffre de poids le plus fort (ici la centaine) est placé à gauche : **Nombre décimal :** $257_{10}=(2×100)+(5×10)+(7×1)=(2×102)+(5×101)+(7×100)$ --- Il en sera de même en binaire : **Nombre binaire :** $1101_{2}=(1×23)+(1×22)+(0×21)+(1×20)=23+22+20=8+4+1=13(10)$. --- Pour compter en binaire, il est alors important de connaître ses puissances de 2 par coeur : --- | $2^{10}$ | $2^9$ | $2^8$ | $2^7$ | $2^6$ | $2^5$ | $2^4$ | $2^3$ | $2^2$ | $2^1$ | $2^0$ | | -------- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | ----- | | $1024$ | $512$ | $256$ | $128$ | $64$ | $32$ | $16$ | $8$ | $4$ | $2$ | $1$ | --- remarque: les couleurs sont codés de 0 à 255 soit sur 8bits= 1 octet --- :pencil:Exercice: Convertir en base décimale le nombre binaire $101010_{2}$ https://www.scienceinschool.org/sis-game/Teacher/card-demo.html --- # Méthode de conversion : décimal vers binaire :one: **Méthode des divisions successives par deux :**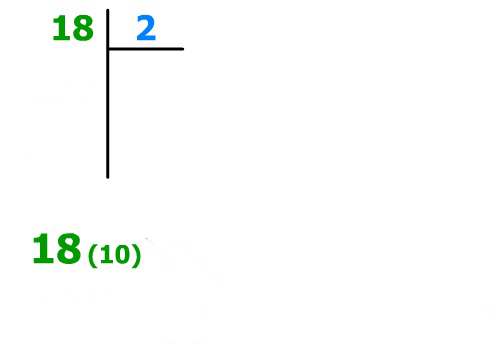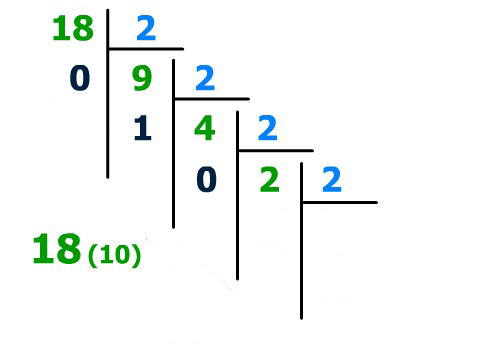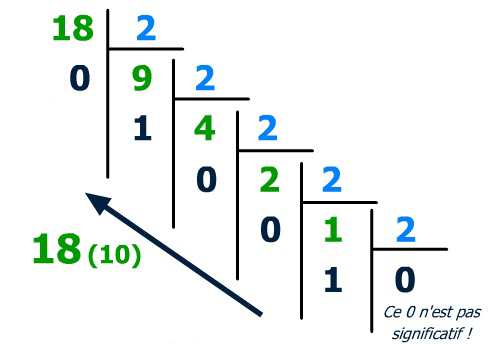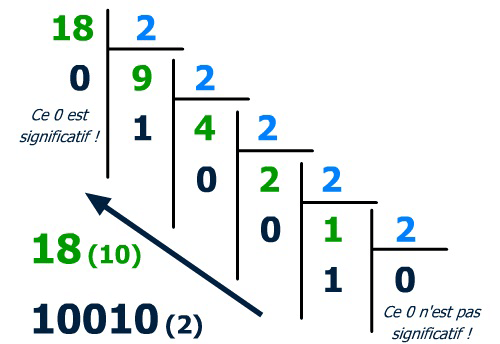 --- :pencil:Exercice: Convertir en binaire le nombre décimal 48 avec cette méthode : --- :two: **Méthode plus intuitive :** Conversion de la valeur décimale 222 en binaire 1. Écrire les puissances de 2 de droite à gauche jusqu'à atteindre la valeur du nombre décimal à convertir. 2. En commençant par la gauche, si la puissance de 2 est inférieure ou égale au nombre, inscrire 1 sous la puissance de 2 sinon 0 et calculer le reste. 3. Poursuivre ainsi en comparant les restes aux puissances de 2 jusqu'à atteindre $1=2^0$ . ---  --- :pencil:Exercice: Convertir en binaire le nombre décimal $48_{10}$ avec cette autre méthode : --- :pencil:Exercice:Complétez les cases marquées par un point d'interrogation et retrouver les écritures binaires des nombres donnés.  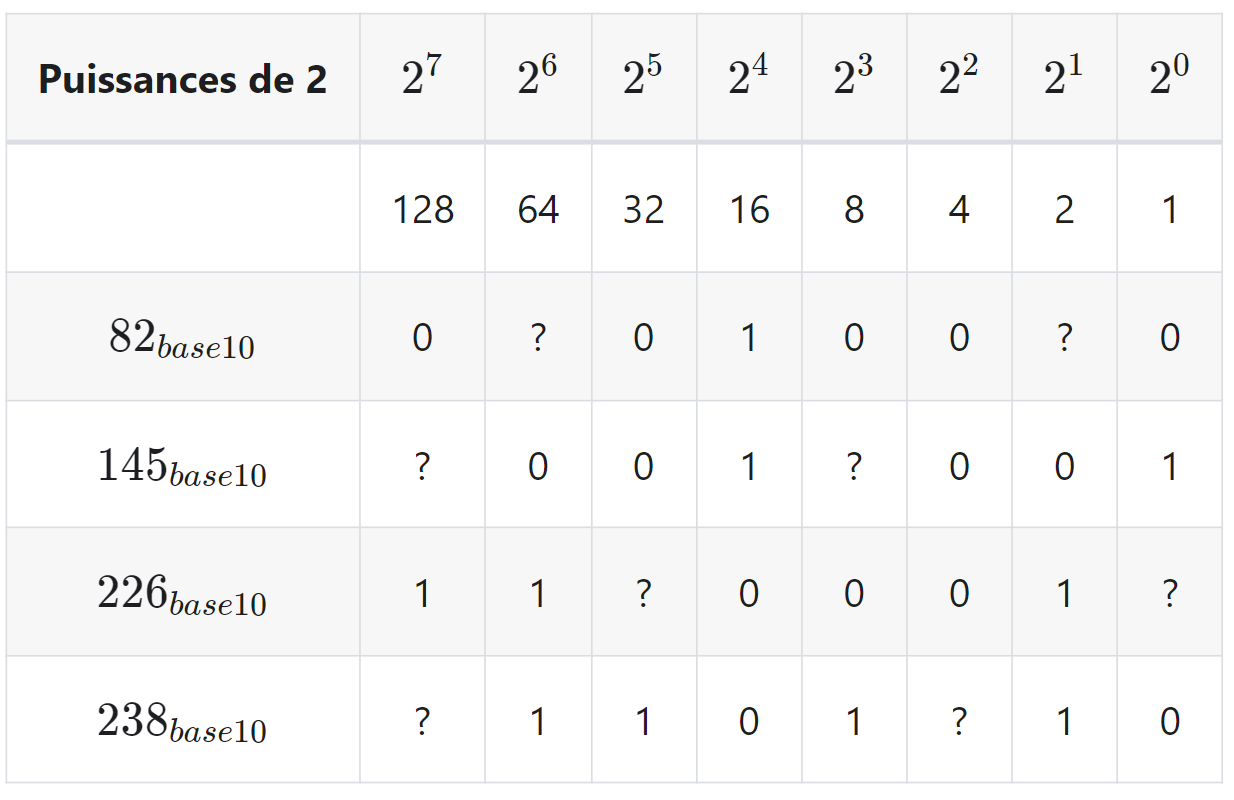--- :pencil:Exercice: Retrouver les écritures binaires des nombres suivants.  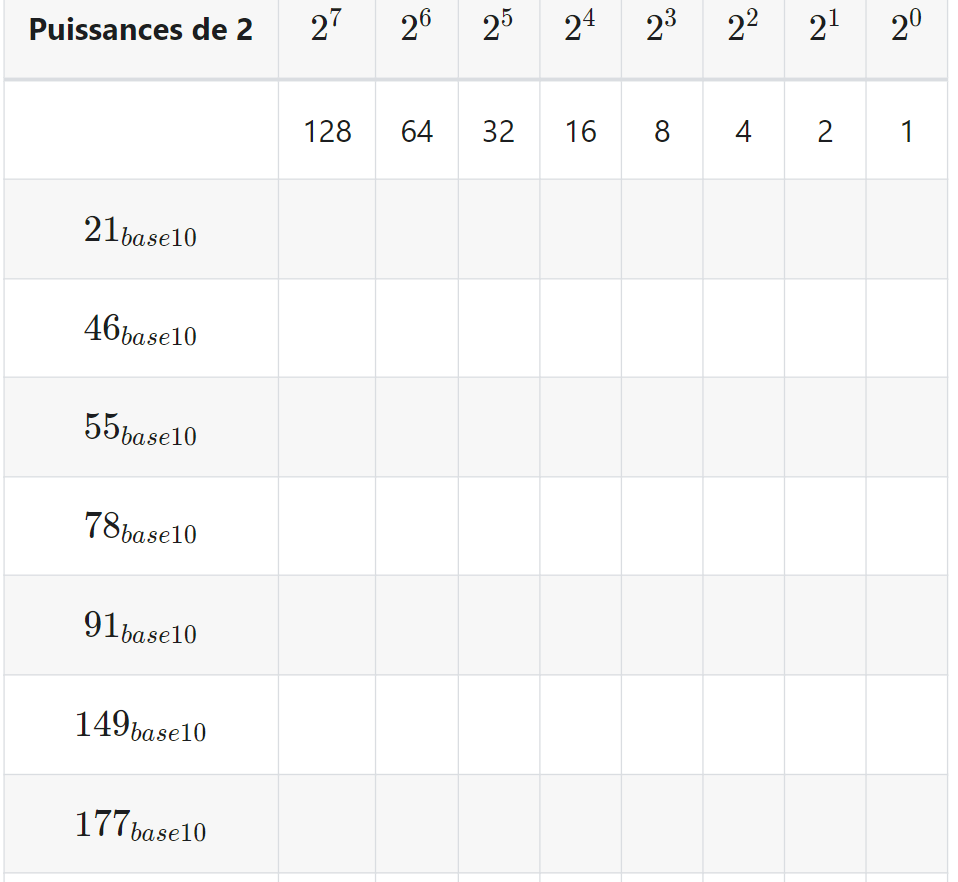--- :pencil:Exercice: le bug de l'an 2038 À l'aide de la page Wikipedia répondre aux questions : - Quel est le plus grand entier signé (positif ou négatif) que l'on peut enregistrer sur 32-bit ? - Convertir le nombre précédent de secondes en années. - Quelle date afficheront les systèmes informatiques concernés le 19 janvier 2038 à 3h 14 min 8 s ? - Donner quelques systèmes concernés par ce bug. --- ## Représentation hexadécimale L'hexadécimal est une représentation plus compacte des nombres. Elle n'est pas utilisée par les machines qui travaillent en binaire mais cette représentation a l'avantage d'être 4 fois plus courte à écrire, ce qui améliore sa lisibilité. L'hexadécimal utilise 16 symboles : les dix chiffres (de 0 à 9) et les six premières lettres de l'alphabet en majuscule. --- | Base 10 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | | --- | ------- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | Base 16 |0| 1| 2| 3| 4| 5| 6| 7| 8| 9| A| B| C| D| E| F| Base 2| 0000| 0001| 0010| 0011| 0100| 0101 |0110| 0111| 1000 |1001| 1010 |1011 |1100| 1101| 1110| 1111| --- Conversion des entiers naturels de la représentation hexadécimale à la représentation décimale : Exemple : $A3_{16}=10×161+3×160=10×16+3×1=160+3=163_{10}$ --- :pencil:Exercice: - Donner la représentation décimale de E_{16} . - Donner la représentation décimale de 10_{16} . - Donner la représentation décimale de 4B8_{16} . --- Compter en binaire c'est comme en décimal : dès que l'on a atteint le maximum (1 en binaire, 9 en décimal) sur un emplacement, il faut ajouter 1 sur l'emplacement à gauche et repartir de 0. 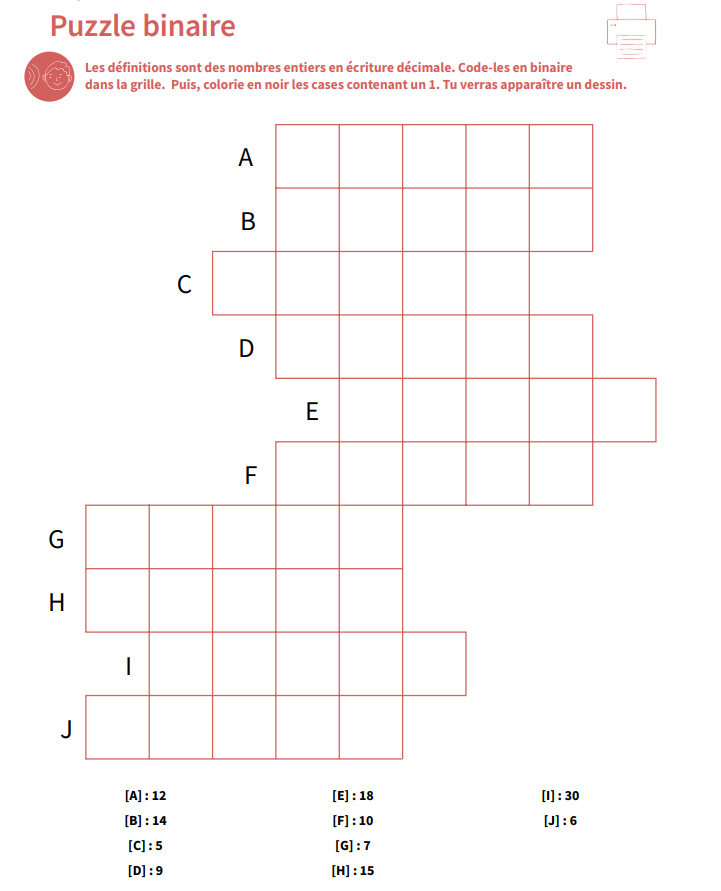---  --- LES SECRETS DU ROBOT PERSEVERANCE  https://docs.google.com/document/d/1PcBTL0yTFrFUBHf8LqIhPYcaZcUS25dbl52TYSMacBQ/edit --- https://drive.google.com/file/d/1i6EzOVhAGLI8Fy-3LF-3geJvhb_Rn2ZK/view --- :pencil: Décodez à l'aide d'une table Ascii 0100110001100101010000000110001101101111011001000110010101000000010000010101001101000011 --- vERSION ELEVE https://codimd.apps.education.fr/s/ZX61O9Zhi --- <iframe width="100%" height="500" src=" https://www.andrewt.net/maths/domputer/" sandbox> </iframe> </iframe> ---