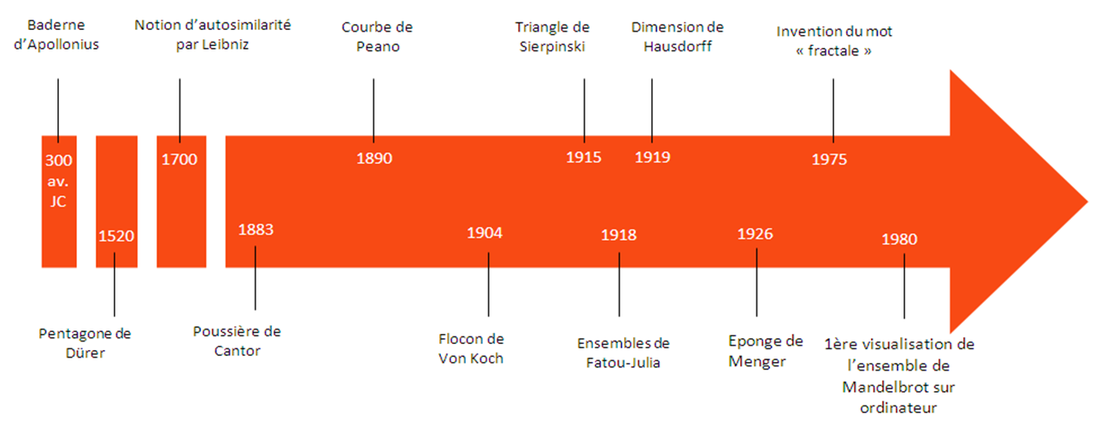
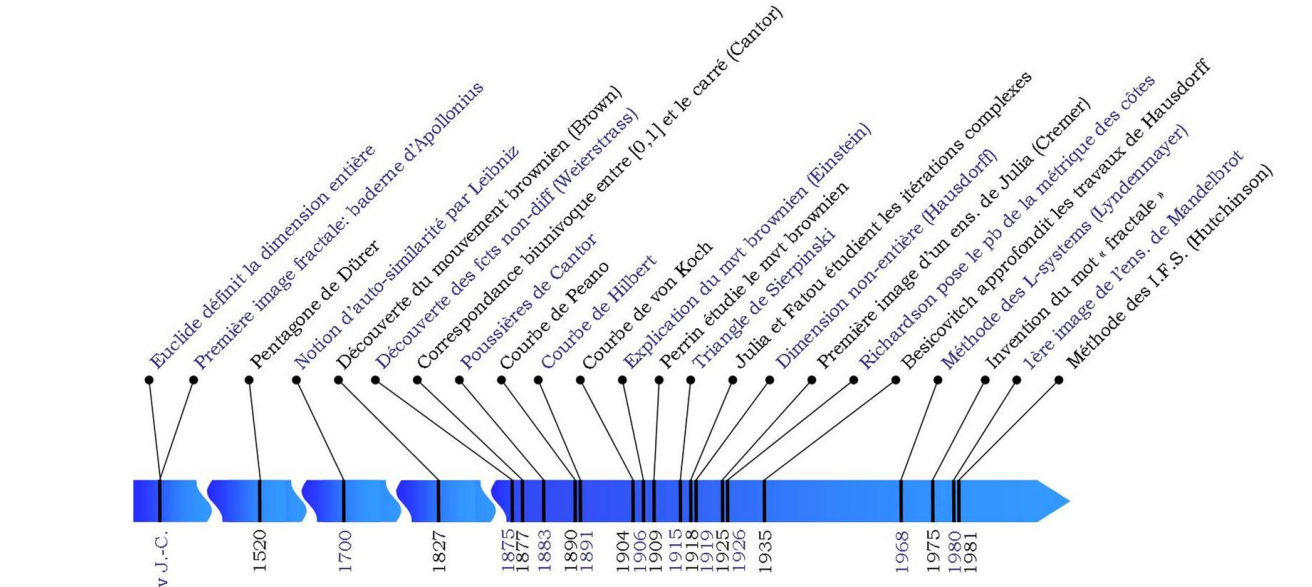
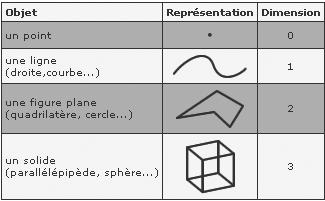
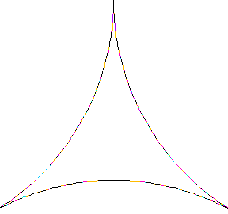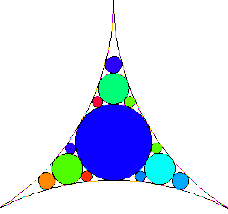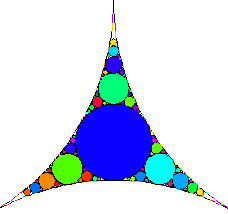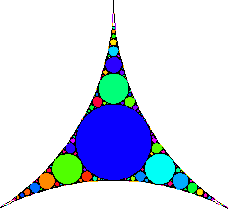
# 2024 # centenaire # MANDELBROT ## Fractales : des origines à Mandelbrot --- https://iremi.univ-reunion.fr/spip.php?article1002  --- # AUX ORIGINES  ----  --- ## EUCLIDE: Dimensions(300 avant J.C.)  [dimensions fractales](http://www.sciences.ch/htmlfr/geometrie/geometrieeuclidienne01.php) --- ## APOLLONIUS (262 avant J.C.)  On part d’un triangle curviligne dont les côtés sont des arcs de cercle. On y inscrit un cercle, tangent aux trois côtés. Puis on construit des cercles, tangents aux côtés et au cercle. On recommence la construction indéfiniment. 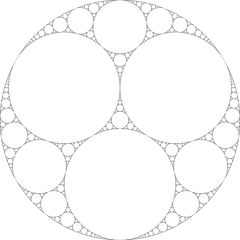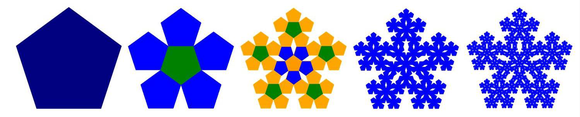----  ----  https://www.fil.univ-lille.fr/~L2S3API/CoursTP/Projets/Apollonius/sujet_apollonius.html --- ## Dürer (XVIe ) Il introduit les Pentagones fractals, appelés "Pentaflake"  --- ## LEIBNIZ : Autosimilarité L'autosimilarité est le caractère d'un objet dans laquelle on peut trouver des similarités en l'observant à différentes échelles >67. Chaque portion de la matière peut être conçue comme un jardin plein de plantes, et comme un étang plein de poissons. Mais chaque rameau de la plante, chaque membre de l’animal, chaque goutte de ses humeurs est encore un tel jardin, ou un tel étang. >68. Et quoique la terre et l’air interceptés entre les plantes du jardin, ou l’eau interceptée entre les poissons de l’étang, ne soit point plante, ni poisson ; ils en contiennent pourtant encore, mais le plus souvent d’une subtilité à nous imperceptible. 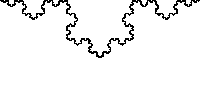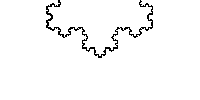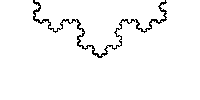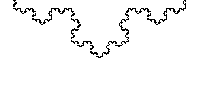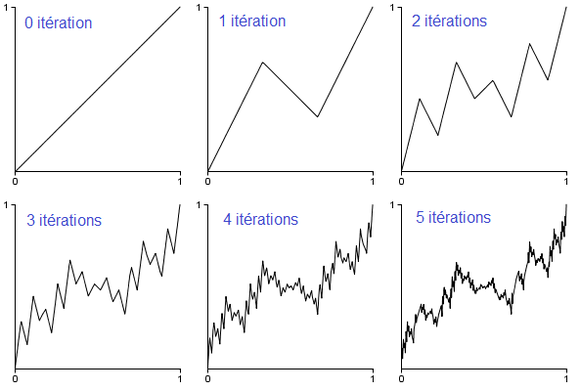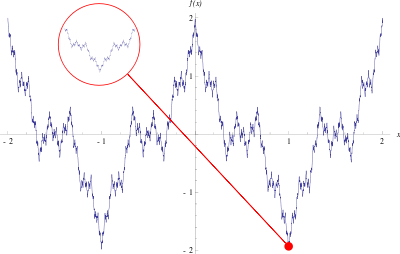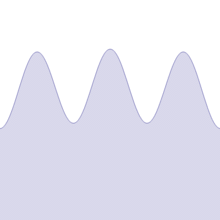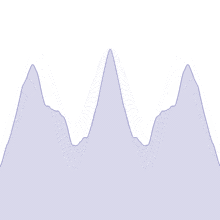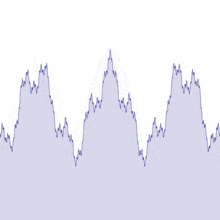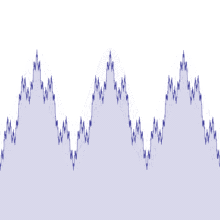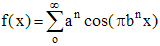La Monadologie (1714) ----  ----  ---- ## Bolzano(1830) Il invente la toute première courbe partout continue et nulle part dérivable  --- ## Weierstrass En 1872 il créé un autre exemple de fonction dont la courbe est continue mais non dérivable  ----  ----  ---- {%youtube QkUeg6IxSMs %} --- ## CANTOR 1845 La deuxième étincelle de la théorie des fractales jaillit il y a cent ans, le 20 juin 1877, dans une lettre de Cantor à Dedekind. Cantor remettait en cause certains fondements de la géométrie euclidienne et notamment la notion de dimension. 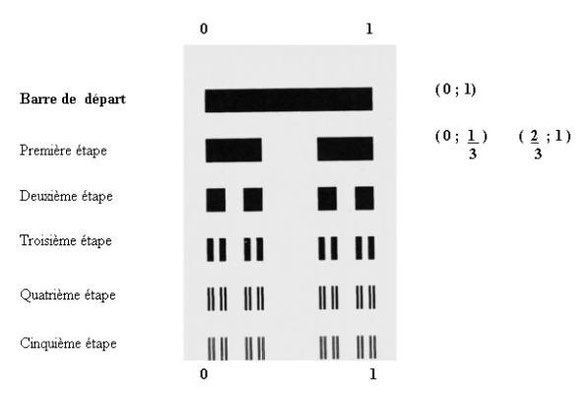---- ## CANTOR  ----  --- ## DEDEKIND  --- ## leur correspondance C’est le 5 janvier 1874 que Cantor pose le problème qui va ébranler toutes les mathématiques : > "À propos des questions qui m’ont occupé ces derniers temps, je m’aperçois que, dans cet ordre d’idées, se présente aussi la suivante : est-ce qu’une surface (par exemple un carré, frontière comprise) peut être mis en relation univoque (en bijection) avec une courbe (par exemple un segment de droite, extrémités comprises), de telle sorte qu’à tout point de la surface corresponde un point de la courbe, et réciproquement à tout point de la courbe un point de la surface ?" ---- Il lui avoue ses inquiétudes quant à la validité du concept même de dimension. Il lui semble avoir démontré qu'un carré ne contient pas plus de points que chacun de ses côtés! Pis: l'intuition et l'école disent qu'il faut deux nombres pour déterminer la position d'un point dans le carré, mais Cantor démontre qu'un seul nombre suffit ---- Le 20 juin 1877, Cantor adresse à Dedekind une démonstration de ce troublant résultat : il existe une ***bijection entre le côté d’un carré et l’intérieur de carré, c’est-à-dire entre un objet de dimension 1 et un objet de dimension 2.*** Le 25 juin, Georg Cantor lui envoie une nouvelle démonstration. ---- N’ayant pas de réponse immédiate, il écrit alors le 29 juin ces phrases tant citées : >“Ce que je vous ai communiqué tout récemment ***est pour moi si inattendu, si nouveau, que je ne pourrai pour ainsi dire pas arriver à une certaine tranquillité d’esprit*** avant que je n’aie reçu, très honoré ami, votre jugement sur son exactitude. Tant que vous ne m’aurez pas approuvé, je ne puis que dire :***je le vois, mais je ne le crois pas !***”. ---- Le 2 juillet 1877, Dedekind répond enfin : >"Cher ami, je suis entièrement convaincu par votre démonstration." --- ## bijection ## exemple: comment relier de manière bidirectionnelle un entier et un nombre pair $1\longleftrightarrow2\times1=2$ $2\longleftrightarrow2\times2=4$ $1\longleftrightarrow2\times1=6$ ... 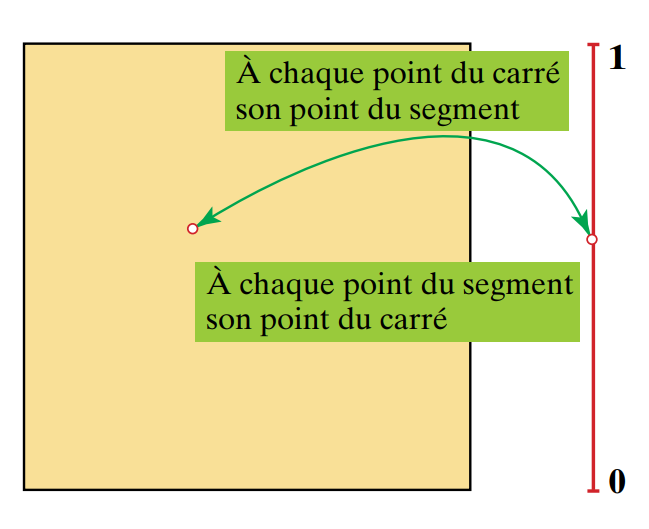$n\longleftrightarrow2n$ ---- ## possible de faire ça entre un segment 1D et un une aire 2D? Par exemple associer à un point d'un côté d'un carré (entre 0 et 1) et n'importe quel point de la surface de ce carré( coordonnées 2D ) <span style="color: black; font-size:200%">0,</span> <span style="color: red; font-size:200%">0</span><span style="color: blue; font-size:200%">4</span><span style="color: red; font-size:200%">2</span><span style="color: blue; font-size:200%">6</span><span style="color: red; font-size:200%">7</span><span style="color: blue; font-size:200%">3</span><span style="color: red; font-size:200%">8</span><span style="color: blue; font-size:200%">9</span><span style="color: red; font-size:200%">1</span><span style="color: blue; font-size:200%">..</span><span style="color: red; font-size:200%">...</span>$\longleftrightarrow$<span style="color: black; font-size:200%">(0,</span> <span style="color: red; font-size:200%">0</span><span style="color: red; font-size:200%">2</span><span style="color: red; font-size:200%">7</span><span style="color: red; font-size:200%">8</span><span style="color: red; font-size:200%">1</span><span style="color: red; font-size:200%">...;</span><span style="color: black; font-size:200%">0,</span><span style="color: blue; font-size:200%">4</span><span style="color: blue; font-size:200%">6</span><span style="color: blue; font-size:200%">3</span><span style="color: blue; font-size:200%">9</span><span style="color: blue; font-size:200%">..)</span> ----  ---- Cantor se voit conseiller par MittagLeffler d'imiter la **discrétion** de Gauss et de ne pas chercher à public ( On sait que le grand Gauss, par crainte des Béstiens (comme il l'écrit un ami) étouffe sa découverte de la géométrie hyperbolique remettant en cause Euclide) --- ## BOLZANO En 1834 que le mathématicien tchèque Bernhard Bolzano construisit une fonction continue mais dérivable nulle part, ce qui signifie que la courbe n’admet aucune tangente. Cette découverte bouleversa les mathématiques --- ## PEANO En 1890, Peano annonçait l'existence de courbes capables de remplir un carré. S'agit-il de “monstres” dénués d'utilité? --- En 1890, Giuseppe Peano livre à la dimension un nouvel assaut. Il décrit une suite de polygones qui paraissent tout à fait innocents, mais se trouvent remplir un carré de façon progressivement plus serrée, de telle sorte que leur limite passe par tout point dudit carré! Un comble! Que pourrait-on concevoir de plus extravagant, éloigné de l'intuition sensible et dénué d'utilité? 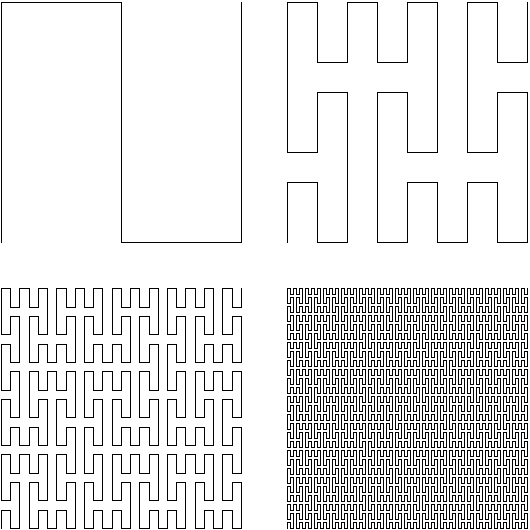--- Péano réussit à définir une courbe qui remplisse réellement tout le carré ! Il y a justement réussi. La courbe suggérée ci-dessous en donne une idée ; elle définit une bijection entre le carré et une ligne très intéressante : deux points proches dans le carré correspondent à des points proches sur la ligne. [ARTICLE CULTUREMATHS NBRE TRIADIQUE](https://culturemath.ens.fr/thematiques/lycee/sur-une-courbe-qui-remplit-toute-une-aire-plane#:~:text=le%20papier%20de%20peano%20est%20court%20et%20concis.%20en%20tout%20au%20plus%20quatre%20pages%2C%20il%20decrit%20l'exemple%20qu'il%20a%20decouvert%20et%20fait%20mention%20de%20travaux%20anterieurs%20relies%20au%20probleme%20considere.%20il%20rappelle%20notamment%20que%20georg%20cantor%20avait%20pu%20etablir%20l'existence%20d'une%20bijection%20entre%20l'intervalle%20%5B0%2C1%5D%20et%20le%20carre%20)  --- https://www.math.univ-toulouse.fr/~cheritat/AppletsDivers/Peano/var-2/ <iframe width="100%" height="500" src="https://www.math.univ-toulouse.fr/~cheritat/AppletsDivers/Peano/var-2/ " > </iframe> ---- {%youtube u-W1jXq5JGg %} ---- {%youtube RU0wScIj36o %} ---- t=342s {%youtube dzymDsEUjKA %} --- ## HILBERT --- {%youtube 3s7h2MHQtxc %} ---- {%youtube x-DgL49CFlM %} ---- {%youtube Nv5_6lH7Elc %} --- - “Une grande révolution dans les idées sépare les mathématiques classiques du 19e siècle des mathématiques modernes du 20e. - Les mathématiques classiques étaient enracinées dans les structures géométriques régulières d'Euclide et les évolutions dynamiques continues de Newton. - Les mathématiques modernes commencèrent avec la théorie des ensembles de Cantor et la courbe remplissant le plan de Peano. - Historiquement, cette révolution fut forcée par la découverte de structures mathématiques qui échappent aux moules d'Euclide et de Newton. - Ces nouvelles structures étaient considérées par les mathématiciens de l'époque comme ‘pathologiques’, comme des ‘monstres’ ... --- - ...apparentés à la peinture cubiste et la musique atonale qui bouleversaient les canons du goût artistique vers la même époque. - - Les mathématiciens qui créèrent ces monstres les considéraient comme importants parce qu'ils démontraient que le monde des mathématiques pures inclut une richesse de possibilités allant bien au délà des structures simples qu'ils voyaient dans la nature. - Les mathématiques du vingtième siècle fleurirent dans la croyance qu'elles étaient allées complètement au délà des limitations que leur avaient imposées leur origine dans les sciences de la nature. --- ## VON KOCH (1904) IL créé la courbe de Koch à partir d'un segment de droite, en modifiant récursivement chaque segment de droite de la façon suivante: 1. Il divise le segment de droite en trois segments de longueurs égales. 2. Il construit un triangle équilatéral ayant pour base le segment médian de la première étape. 3. Enfin, il supprime le segment de droite qui était la base du triangle de la deuxième étape. ----  --- - L'ensemble de Cantor est intermédiaire entre le point et la droite, et la courbe de Koch entre la droite et le plan, et pendant la période qui suivit leur “invention” mille et une autres manières d'être intermédiaire furent identifiées par les mathématiciens - En particulier, nul ne les considéra comme suffisamment importants pour éprouver le besoin d'un terme générique pour les désigner –. jusqu'à ce que mes travaux me forcent à les baptiser, enforgeant le terme # fractales. --- ## Sierpiński(1915) Cette construction consiste à prendre un triangle quelconque et à lui retirer le triangle formé par les points milieux de ses trois côtés. Pour chacun des trois triangles ainsi formés, on retire le triangle central de la même façon et on poursuit le procédé jusqu’à l’infini.  ---- La carpette de Sierpiński / Le tapis de Sierpiński (1916)  ----  ----  --- L'éponge de Menger, parfois appelée éponge de Menger-Sierpinski, est un solide fractal. Il s'agit de l'extension dans une troisième dimension de l'ensemble de Cantor et du tapis de Sierpinski.  --- Le plus intéressant avec cette éponge, c'est que lorsqu'on la coupe transversalement. Regarder bien la forme de la section :  ---- {%youtube IZHiBJGcrqI %} ---- 8 manières de construire le triangle de Sierpinski http://eljjdx.canalblog.com/archives/2008/08/03/10122451.html ----  ---- {%youtube 8D_ThIqoJL8 %} ---- On peut les qualifier de “chimères”, car ce sont des “figures intermédiaires” entre points et lignes, lignes et surfaces, ou surfaces et volumes. Mandelbrot les baptise ***fractales.*** UN OBJET PEUT ÊTRE QUALIFIÉ DE FRACTAL S’IL POSSÈDE LA PROPRIÉTÉ SUIVANTE : QUEL QUE SOIT LE NOMBRE K, IL CONTIENT UN MORCEAU QUI EST EXACTEMENT SA RÉDUCTION DANS UN RAPPORT PLUS PETIT QUE K. 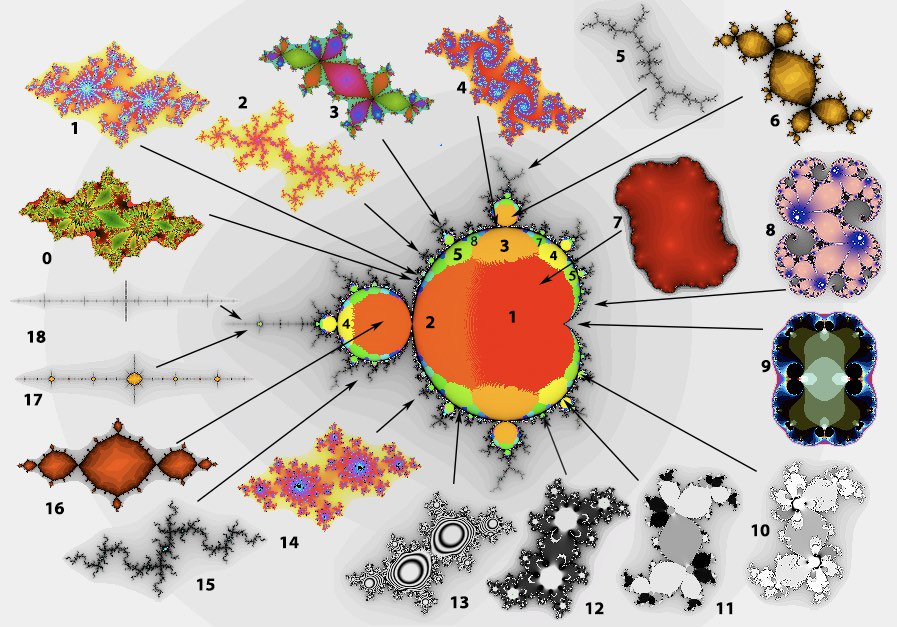---- <div style="max-width:854px"><div style="position:relative;height:0;padding-bottom:56.25%"><iframe src="https://embed.ted.com/talks/lang/en/benoit_mandelbrot_fractals_and_the_art_of_roughness" width="854" height="480" style="position:absolute;left:0;top:0;width:100%;height:100%" frameborder="0" scrolling="no" allowfullscreen></iframe></div></div> --- ## ensemble de Julia ---- ## Liens entre l'ensrmble de Mandelbrot et l'ensemble de Julia  ---- https://www.dynamicmath.xyz/complex/mandelbrotjulia/ <iframe width="100%" height="500" src="https://www.dynamicmath.xyz/complex/mandelbrotjulia/ " > </iframe> ---- https://twitter.com/jcponcemath/status/1153282413834858497 --- https://fr.mathigon.org/course/fractals/mandelbrot --- La suite https://codimd.apps.education.fr/p/rtxcY7l4r