# Perlin 2D
---
**La motivation ?**
[Minecraft](https://youtu.be/CY4wxHPVXiQ?si=EWRDTvAxE-jnJ72j&t=258)
---
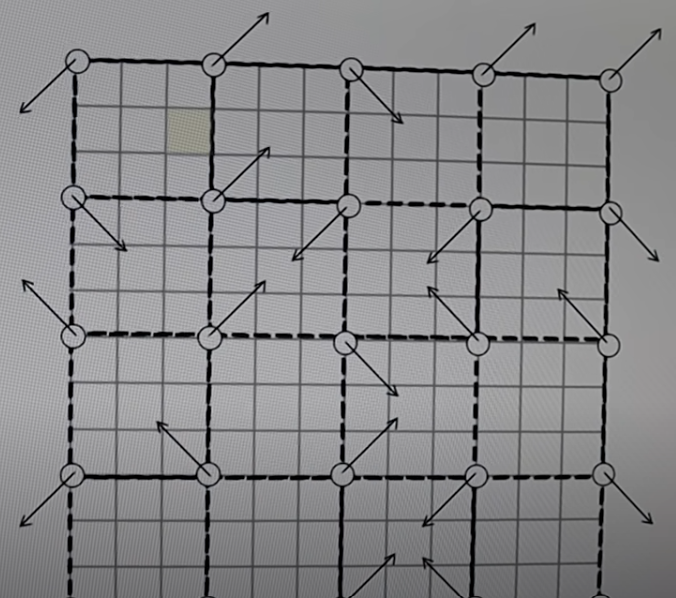
- Imaginez une grille en 2D, comme un quadrillage dessiné sur un papier.
- Chaque croisement de lignes (point de la grille) est associé à une "direction aléatoire".
- Cela peut être représenté par un petit vecteur (flèche) pointant dans une direction donnée.
---
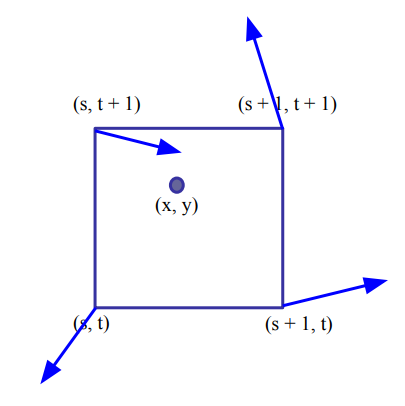
**Points à interpoler :**
Les pixels $(x,y)$ d’une image ou des points dans l’espace 2D ne tombent pas forcément pile sur les croisements de la grille.
---
**Points à interpoler :**
Le but est de calculer une valeur pour ces points en se basant sur les vecteurs autour d’eux.

---
## **Comment interpoler cette valeur $(x,y)$?**

---
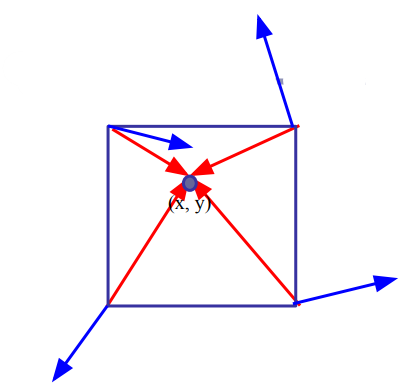
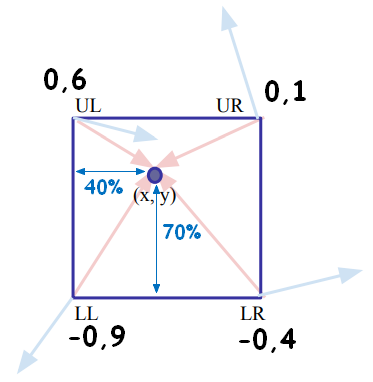
### Avec des produits scalaires !
Les flèches rouges partent des 4 coins vers le point $(x,y)$
---
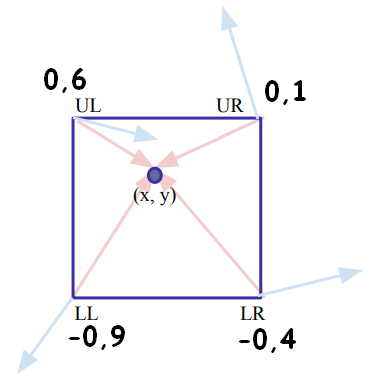
### Avec des produits scalaires !
On va calculer dans chaque coin, le produit scalaire de la flèche rouge et de la flèche bleue !

----
***Pourquoi le produit scalaire ici ?***
---
---
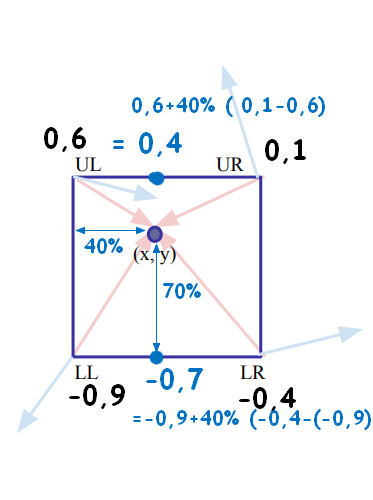
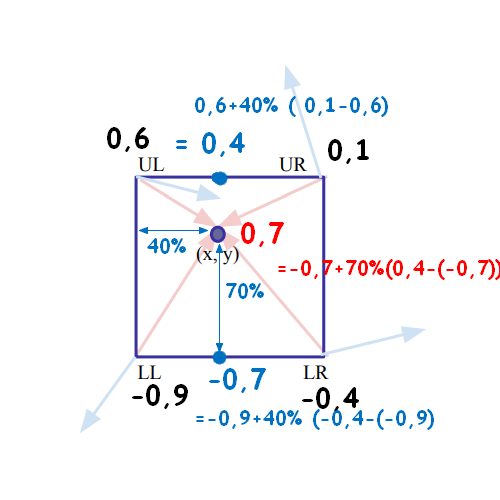
:A:**Interpolation linéaire**(simple)
---
---
---
**on fait ça dans toutes nos cases ...**
---
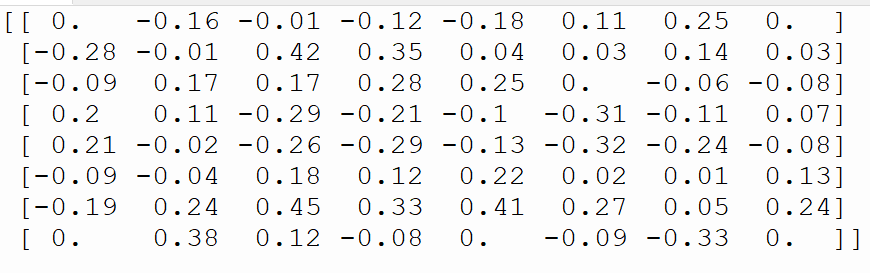
**on arrive à ça!**
---
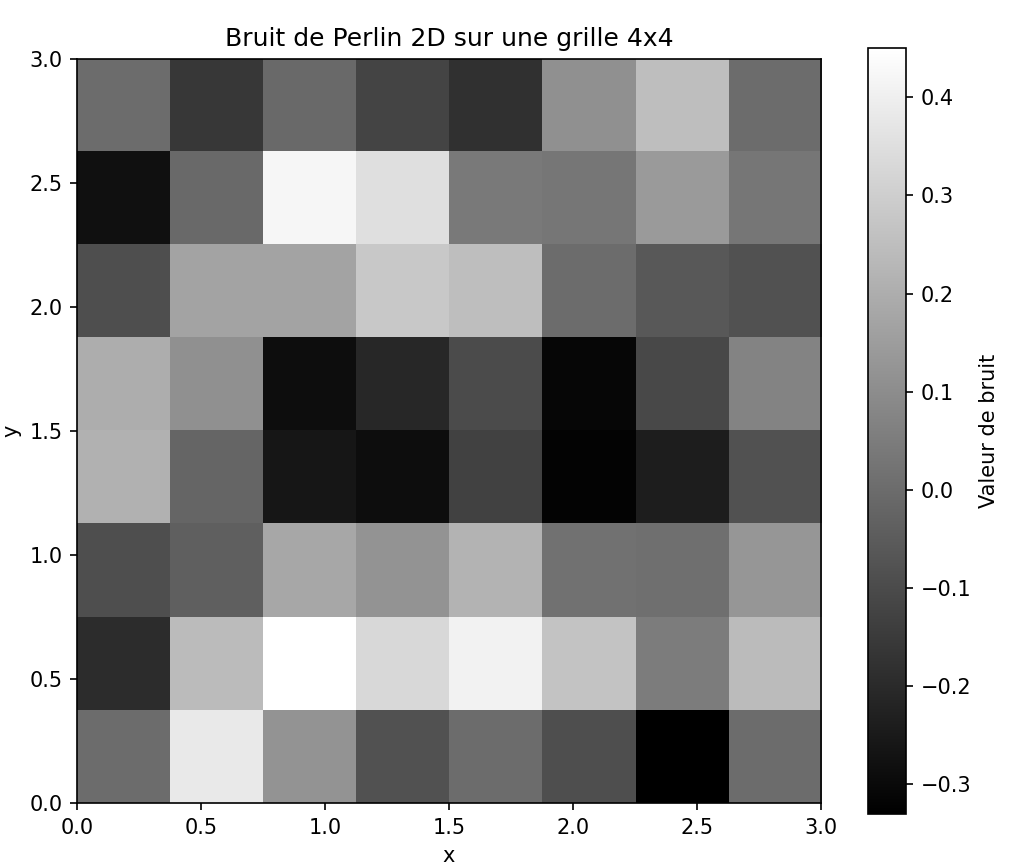
---
Une opération mathématique plus loin, on a un tableau d'entier qui peuvent représenter des hauteurs
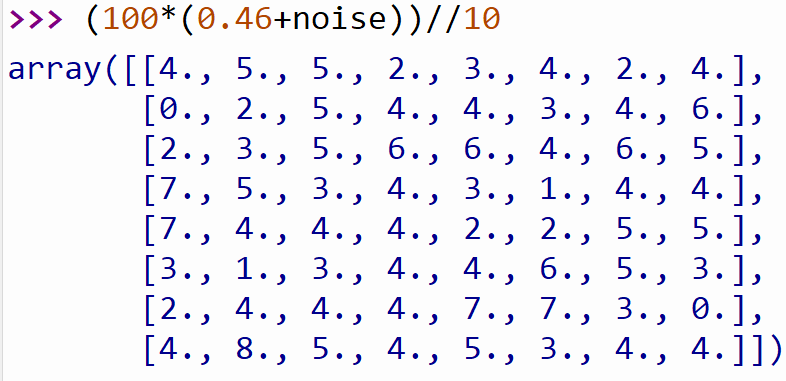
---
Plus qu'à représenter ça
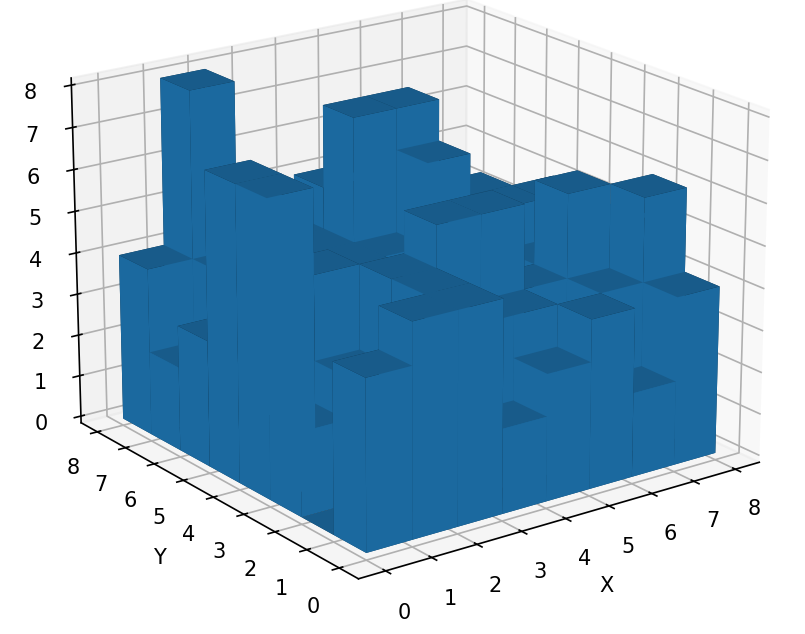
---
https://www.pyxelstudio.net/studio/m7kdpf
<iframe width="100%" height="500"
src="https://www.pyxelstudio.net/studio/m7kdpf" sandbox>
</iframe>
---
https://cpge-paradise.com/TIPE/anwar_kardid/PPT_kardid.pdf
---
https://notebook.basthon.fr/?from=https://raw.githubusercontent.com/anwarden/Generation-procedurale-dans-les-jeux-videos/refs/heads/main/Labo%20TIPE%20Anwar%20Kardid.ipynb
---
voir aussi ==***Déplacement du point médian (Midpoint displacement)***==
---
https://bitesofcode.wordpress.com/2016/12/23/landscape-generation-using-midpoint-displacement/
https://stevelosh.com/blog/2016/02/midpoint-displacement/
https://linuxfr.org/news/je-cree-mon-jeu-video-e10-generation-procedurale-de-carte-partie-1#m%C3%A9thodes-%C3%A0-base-de-placement-de-point
[super ](https://notebook.basthon.fr/?ipynb=eJy9OGmPqljaf4XX_lI11i3cxZupTg7ggriAhVt13XQQDkeUTRYRO_e_v88BrdKa7k4mMxkTlfPs-3n0j5KBHScqff_tj5KLY93UY730_Y-fTzn89zgLcOl7ydXDvemnXumpFPlJaFDYP20r1F387jGMbb68l2zPsT3co7DuSXcDB7-XKDK2YwcDXsrxTE7A3FGkthlvgaJar1QKyBbbZBsDqHWFRKEBx20cB9F3lnWwHnrPrcbGjs1QJ773bPguq4exbTg4YuEQJDEOv0WGjT0Ds0HoG9hMQt35RrCHQz22fY91bTPwbS_-ZtpR4OgGdjEcbO-b72GAwSkCMua99Ou790-2cBceSz-f7mJVisMkirFZ-g4P-EvkDN_Et1GzQt9lFGnE2G7ghzEjuTqBGF5OgHjOIWKop4weMR-HD5JQ90zf_Th6iRtklNIL3r1cuKvH26t0y_H98AI3fMfBBnU8uqJNfEhA-btnYgv4bO_h8TsNNmSU6l3SvDAvTLNav4EO8twAuNZsFeDQT8jWw1FEgZAwrwD_wqSYsT07tnXHPmNGdxwm3uJLciMm9plKQXmFvDC_VX7841P3pyRwmvJ6t_KoLMsOozjHOjo83Igu4sQcdSfB0Z0a0AGaCvwz_YISeKg8UX8e7wlvovCNqf4d143HRoj1GLxlILYJZnwrNzSv_QgTWmIRJfMwNqmdUbIx7aNt4kLEAZTkaXl4vPdeN80bjy-SqAA7vnA-60GAPfOBWnVv-dNnih5vxHp-Si0hPgjOCXJFHwYxWDe2V00FT7q1HfAFew-HR-b_XpjKpVzoy8FWDIpo5J4ucbrUxOE58AOKfnj8JDdAKA4B-0AxTLnghO_qI8OyTO1qZmFqhOPc-2vLUsfpWT9CM5OPKMepz0AIok_WayoLdTSFD1cQ1fsDFF7PuQE__kz7R_XRJEQ-zK9P__5O1VdI-Wv9fPuUcxuzx3v1duFcPiavnl4LwI4YkhdcCGDdY2qXNokZA04b_JlO81MkCCyi_S3PGvMrU7tJ5KWSqRiojmvdeTj9UsSXFORl_kRJQxixRtGXuusnYB0Y-2eRui_XonCKGD0VI-vhpn5oOh4fH_-K-8p3Kby_Zr9WvWV7MImywmCYfDRwOPoYS9dJR5s9RxfzLrqWzW1vPd1OxMcr53MEVfnwXopxFD8HHnkvPcEdokz676Ubmq2fFi3-7v3CwCWWRnngiH2EuF_nGNw-FGgXl8Qvd-MTJCSOSVPs-aGbj8R8oABgg-MUg5hKXrk593PBVoz6f9Ox2ztBgXqwPQLRqdfuxt6HEfdG0hrRoUzh2YXZ7SZubpOrn_Ln2_FMUwMXmg3XZ3bneV6GIbw3fpJ3vplfiPc3x4f-L_5cDL7zCOr-Fnc_v6-D2fA9GC7x1ytLhwYIbRzR2s5HUXQJeuD4cXztsgsGLrQH--nzPoHpYvkhY8M1RhuD4PtZ_fjjz2e-4YewtHxGEz5Ag5PB4kMHAA1ZTm84fgSWwbYT4NDJbk15tj2wO7-x6LtybagL9tpNX--Nymfn5C2R7yPPMAugvke0sB_-qmgu8mmqrnx0j3mmH8B0g36-uPJQ2AI9bDvOCywSH6pDHCchuOpe--Uj2RH4DbUR6hnNByxDmzxOCVxcl0jBwAJS2ArjCxrmKCwim49-AmdGfopDHiaWeR31sE6E5F95rgxzCFfBQKVgqBPQD7jwK31k6M6_tGW8hTRdIl805Gfx0p3y6d6mp3uN13aEdqJlHzzDQ852CSm01gWun27heb0BhuK_Ue4CDLJnF8ydGqC5s-JLLn570Aspj8w_PmWwFy3lL1GlRa_Toqf2_CiyWOybsBvjEzYSupf-btBLo_S9_lSCRocNvvhZUjxfF-piV89-z5fvp9LHDo5PMQsI26M_TT726OLzMkZc2MVfRkwEcX6BnfYEqxsDNVI5VbutClev_AryckoWpjaIsRf8dJZW5D7xEbwmr_Ntd07giXTho4sElL-UqXXowXfvvHe66mLW8KZ1U1ttdpMt31u_2l6vsers2nYkCtrIj-Ys6Qrb-bRTJo225mzPfXOx3AdiOzk1JdLesDO-IfJyF5m8bu_QYD73pYZQ7fXRlATqLB0c_vu4vtjUzg0kbEk4GZyDFA14t8zz585Al7U6N8YTMquTtE06KurudhtOhojUt9ECITyNRmlvMJwjvmVviTvilPK-NyJo2OdWaOH2hjJbWVtEWB8bFTZCXbb_1u3y0nmro5lGsjeUyn2EtCyBuG7WYo3v9revZEdG44FWV_ks5QWHHyBTnw7Km9orWFlV-odIqK60dKa9JikyuVTzVV5jnTXiDfCvG68Wvlh1DwiZsxnJpj0wdN54m6RD3tyeElXyU6mtIGGHJDOey2NBrpyAZNZ6O-0lfhZSY4I006RVrltby4POsp_rhpgJG2tFwHZnUcl6sjBF9mmuyKOJQ1AP95cgaOn7KRJNteP5GY2R7_sjVufbyqSb26SpK6sq1pbqcC6hlpDs4jNR3tbES81GWnEWJruc2yKy1pZ4TkiwyXTsxwND4WKI_6RpGcdD2uH8Bl_j4jW78dhZ3e6dBqY4brfsZewo4TQb1lSEJ4P2WydOUS-eDE-aU9F8Cb11uhlqNVAtcdiG2Yw0XpttuSg7Wj1N6bV2WWNVCXy03AVsqxdxfsBqjePSGk3ZV5egjbKy9od-vHLUfrWMZG7QbvfanMyS48bsVBp1I5BkvbMIm6zXnqCjaSycpB6yJ8s1VwE6tFhePNiLVZkTNUvqV4R21ctalt7s-LtTyJXVvjXoeIeWPmiIkV31T-fGwBM2Znq0VhWtPU1Erwah01ZC2mkbynRoms4uY21l9paOu36_dWwoVakslF8nu0aYTKK26-piJR226ousTQ7huWV5kSSJc06cDkIyWdW56XHDKYmbRXjidc9slZ2mRsvnYnsxSydJxs0dtsuymbf0gvpqpSDfsuL6qdw9dZKBKy2trJ3q1vyQqa87qx3Xw4EzU9TjeDKdls0xJ2Beigm_SmGqmKlCWAE3EHJ2Mxm-qokqSxJit3JDdJWK682qMGniihChmqsO10iL54ItIOVV6nXHKNmrcvraGqNFhMq2KkkNie8izSZzhMKGtEUIulkeNHio2qi8i8Wz0hlzPMiUTaGdiq5VGewHQLzgNBMZZ9YNURtGWiKEPujvOOuVgUZ-8IaEI0kC0muMDiq_QYLgqxH0kN2LkCzz_RMaqtISdPrdHfiC9ivSj4g42lJb1aQrq3LPp3yv-3mI5KXQMyifHiH-dbRQga-XRcCXLBDwocNW2Au9V7RMkRt0ZYKqaLtCwoG8HhA_txdjJLf4qQdKh5WUDyVenqs-Ib2Ap_r0PegbzddUXyua-0iZCyxSh2BrzJU5sHLrlQnESt68CZmAkrJeFl2x3OGqBlImxzWWzzDPK-Mlx_MTsR_2Db4Zs3IgwhgYHt5ihCrjmkH11t7CdLpWGvF5sUaVWieOwjEML7W-SLvdyqQ5fksHbp2bGNNUjDVwVG4JI0xtFRtuojYJO6mPI3Us-UPuzSTiuV1zBZoPaKojQWKLczhUPg7LAwP1W-N6UwT_2l66UpHYKcMAYjf7hPALAnW5WHcbcF2vOt1N0B7JU2UtLU8uO6n2bBg57YZMRjW51RCMlWsdqjFBUlM7EuVcDvTqGHWVuUeW-q5xbIrVUWs15XfzaX3Kd0-sP5aERThuJcsjToz6ylRVfteb1XoRGbAwT2pldtMZHabqsGY3U2nVrL9VoiarNF-XDjtJe1WRn6cLh-jV0ah1VEaZJtQVr1Mb1LVle7vcWkrTrx99Dqmn2lrFXBhntVl7wdWJr01jqNZW2xD6_HJ7PpLM2TaHdTObpSAynQ_e0q6wV_g3NGUn8uBg8qumy9Z7UwkZExbtZ-aag_6VOU2I_aXWskR219pDv_ztayoIbNrtRIM4RA5v9lIK5IezebMb7oeEkJeX0s-nu_9Hf_74T_4F_LOtx0sc53bx-R8o-HHnU2mP4WeGEwXYoCdPd6mkIIN11avTVeuyeV0QSo5gKMaBpS-BvemDvPQT7PM2Fl1rQXPj8_A7rIx-WPpe-_n_YpRw9Q)
{"title":null,"tags":"perlin,bruit,matrice,image","type":"slide","slideOptions":{"theme":"black","parallaxBackgroundImage":"https://minio.apps.education.fr/codimd-prod/uploads/upload_ed4f025d8b8a11c88f166a2c06f94e22.jpg","transition":"slide","overview":true}}