<style> mark{ background: yellow; font-weight: bold; } // https://lucidar.me/fr/web-dev/css-color-list/ </style> # DNB Juin 2025 Asie : une correction du sujet de mathématiques > *Conçu à partir du sujet transmis par M.Turpin et proposé par Christophe Poulain (c) CC By-Nc-Sa 4.0 puis modifié avec le [sujet original](http://college.valdugy.free.fr/IMG/pdf/dnb_2025_asie_original.pdf).* > *Merci aux relecteurs : Lison, Cassandra, Timothée, Chloé, Maëlys, Raphaël et M.Benoist.* > (c) CC By-Nc - 17-18 juin 2025 - Keops ([E.Ostenne](mailto:emmanuel.ostenne@ac-lille.fr?subject=CodiDNBjuin2025)) # Exercice 1 (16) points) Cet exercice est un questionnaire à choix multiple (QCM). Aucune justification n’est demandée. Pour chaque question, quatre propositions (A, B, C et D) sont données. Une seule est exacte. Recopier sur la copie le numéro de la question, ainsi que la lettre de la réponse. ## Question 1 Dans une urne, on dispose de 4 boules bleues, 6 boules violettes, 7 boules rouges, 3 boules jaunes, toutes indiscernables au toucher. On tire une boule au hasard. Quelle est la probabilité d’obtenir une boule violette? | Proposition A | Proposition B | Proposition C | Proposition D | |:---------------:|:--------------:|:---------------:|:----------------:| | $\dfrac{6}{14}$ | $\dfrac{1}{4}$ | $\dfrac{3}{10}$ | $\dfrac{14}{20}$ | :::success ::: spoiler ++Correction++ <mark>1-C</mark> *La justification n'était pas demandée.* 6 boules sont vertes sur les 20 contenues dans l’urne. La probabilité d’obtenir une boule violettes est égale à $\dfrac{6}{20}$, soit $\dfrac{3}{10}$ ( ou 0,3 ou 30 % ). ::: ## Question 2 Calculer 70 % d’une quantité revient à multiplier cette quantité par : | Proposition A | Proposition B | Proposition C | Proposition D | |:-------------:|:-------------:|:-------------:|:-------------:| | 0,30 | 0,70 | 1,70 | 1,30 | :::success ::: spoiler ++Correction++ <mark>2-B</mark> *La justification n'était pas demandée.* 70 % = ++0,70++ (ou $\dfrac{7}{10}$) ::: ## Question 3 On considère la série suivante composée de 5 valeurs : 7; 18; 12; 13; 15. | Proposition A | Proposition B | Proposition C | Proposition D | |:-------------------------------:|:---------------------------------:|:---------------------------------:|:--------------------------------- | | L’étendue de cette série est 8. | La médiane de cette série est 12. | La moyenne de cette série est 53. | La moyenne de cette série est 13. | :::success ::: spoiler ++Correction++ <mark>3-D</mark> *La justification n'était pas demandée.* A/ e=max-min donc e=18-7=11. B/ On range dans l'ordre croissant : 7; 12; ++13++; 15; 18 donc 13 est la médiane. C/D/ moyenne des valeurs : 7+18+12+13+15=65 et $\dfrac{65}{5}$=13 d'où la réponse D convient et non la C. 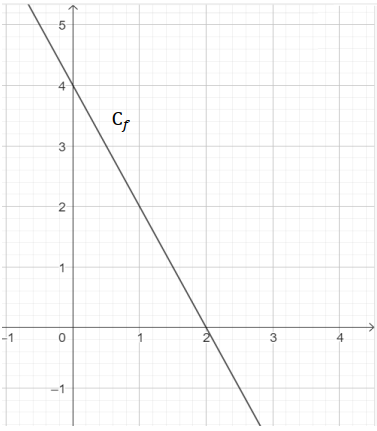::: ## Question 4 Une fonction affine 𝑓 a pour représentation graphique la courbe C𝑓 :  L’expression de la fonction 𝑓 est : | Proposition A | Proposition B | Proposition C | Proposition D | |:-------------:|:-------------:|:--------------:|:--------------:| | 𝑓(𝑥) = 2𝑥 + 4 | 𝑓(𝑥) = 4𝑥 − 2 | 𝑓(𝑥) = −2𝑥 + 4 | 𝑓(𝑥) = −4𝑥 + 2 | :::success ::: spoiler ++Correction++ <mark>4-C</mark> *La justification n'était pas demandée.* 𝑓(𝑥) est affine donc bien de la forme 𝑓(𝑥) = a𝑥+b. D'après le graphique, 𝑓(0)=4 donc b=4 : 𝑓(𝑥)=a𝑥+4. Seules les réponses A et C conviennent. D'après le graphique, 𝑓(2)=0. Remplaçons dans les expression proposées : - proposition A, 𝑓(2) = $4\times2+4$ = 12 donc A ne convient pas; - proposition C, 𝑓(2) = $-2\times2+4$ = 0 donc C convient. > *Remarque : on aurait pu tester directement quand 𝑓(2)=0 i.e; remplacer 𝑥 par 2 pour chaque proposition :* >- *proposition A : 𝑓(2) = 2×2+4 = 6* >- *proposition B : 𝑓(2) = 4×2-2 = 6* >- *proposition C : **𝑓(2) = -2×2+4 = 0** * >- *proposition D : 𝑓(2) = -4×2+2 = -6* ::: # Exercice 2 (24 points) Dans la figure ci-contre qui n’est pas représentée en vraie grandeur : — Les points G, C et E sont alignés. — Les points F, C et D sont alignés. — Les droites (GF) et (DE) sont parallèles. — Le triangle CDE est rectangle en D. — CD = 21,6 cm, CE = 29,1 cm et FC = 17,2 cm.  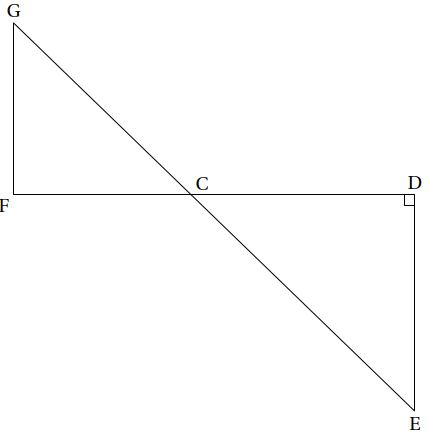1. Montrer que la longueur DE est égale à 19,5 cm. :::success ::: spoiler ++Correction++ Sur l'énoncé ou au brouillon, on annote la figure avec les informatiqions du texte. Dans le triangle CDE rectangle en D, d'après la propriété de Pythagore, CE² = CD² + DE² 29,1² = 21,6² + DE² 846,81 = 466,56 + DE² DE² = 846,81 - 466,56 DE² = 380,25 DE = $\sqrt{380,25}$ <mark>DE = 19,5 cm</mark>. ::: 2. Calculer l’aire du triangle CDE. :::success ::: spoiler ++Correction++ $Aire(triangle)=\dfrac{base \times hauteur}{2}$ $Aire(CDE)=\dfrac{CD \times DE}{2}$ $Aire(CDE)=\dfrac{21,6 \times 19,5}{2}$ <mark>Aire(CDE = 210,6 cm²</mark> ::: 3. Calculer la longueur GF arrondie au millimètre près. :::success ::: spoiler ++Correction++ On reconnaît une configuration de Thalès dite "papillon" ou "sablier". Les droites (FD) et (GE) se coupent en C et (GF)//(DE), donc d'après la propriété de Thalès : $\dfrac{FC}{CD}=\dfrac{GC}{CE}=\dfrac{GF}{DE}$ $\dfrac{17,2}{21,6}=\dfrac{GC}{29,1}=\dfrac{GF}{19,5}$ donc $\dfrac{17,2}{21,6}=\dfrac{GF}{19,5}$ d'où $GF=\dfrac{17,2 \times 19,5}{21,6}$ donc $GF \approx 15,53$ soit GF est <mark>environ égale à 15,5 cm</mark> au millimètre près. ::: 4. On trace une droite (𝑑) perpendiculaire à (FC) avec un logiciel de géométrie dynamique. La droite (𝑑) coupe le segment [GC] en A et le segment [FC] en B. En affichant l’aire du triangle ABC à l’aide du logiciel, on obtient 23,4 cm².  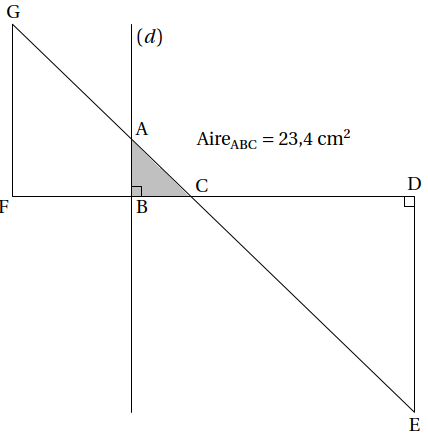a) Montrer que l’aire du triangle ABC est égale à $\dfrac{1}{9}$ de l’aire du triangle CDE. :::success ::: spoiler ++Correction++ Calculons $\dfrac{1}{9}$ de l’aire du triangle CDE : $\dfrac{1}{9} \times 210,6=23,4$ donc <mark>l’aire du triangle ABC est bien égale à $\dfrac{1}{9}$ de l’aire du triangle CDE</mark>. ::: b) On admet que les triangles ABC et EDC sont semblables. Déterminer la longueur AB. :::success ::: spoiler ++Correction++ Le triangle ABC est donc l'image du triangle CDE par une homothétie de centre C. Vue la configuration de Thalès "papillon" ou "sablier" qu'on observe puisque (AB)//(DE), le rapport d'homothétie est négatif : appelons-le k. Si les longueurs du triangle CDE sont multipliées par -k pour donner les longueurs de ABC, l'aire du triangle CDE est multipliée par k² pour donner l'aire du triangle ABC. Donc k²=$\dfrac{1}{9}$ d'après la précédente question, soit k=$\dfrac{1}{3}$ ou $\dfrac{-1}{3}$. donc k=$\dfrac{-1}{3}$. Dès lors, AB=$\dfrac{1}{3}$DE donc AB=$\dfrac{-1}{3} \times 19,5$. Donc <mark>AB = 6,5 cm</mark>. ::: # Exercice 3 (20 points) Dans cet exercice, toutes les longueurs sont exprimées en cm. 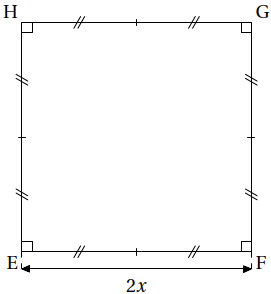On considère : — le rectangle ABCD tel que AD = 𝑥 et AB = 16 − 2𝑥; — le carré EFGH tel que EF = 2𝑥. 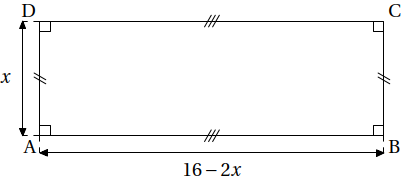 -  ## Partie A Dans cette partie, 𝑥 = 1,5 cm. 1. Calculer le périmètre du carré EFGH. :::success ::: spoiler ++Correction++ EF = 2𝑥 d'après l'énoncé donc EF=$2\times1,5$=3 cm. Périmète($carré$) = $4\times côté$, donc Périmètre(EFGH)=4×3 soit <mark>Périmètre(EFGH)=12 cm</mark>. ::: 2. Calculer AB. :::success ::: spoiler ++Correction++ AB = 16-2𝑥 d'après l'énoncé : AB = 16-$2\times 1,5$ AB = 16-3 <mark>AB=13 cm</mark>. ::: 3. Construire en vraie grandeur le rectangle ABCD. :::success ::: spoiler ++Correction++ On constuit le rectangle de longueur AB=13 cm et de largeur AD=1,5 cm. Sur copie quadrillée, on peut utiliser les carreaux pour les angles droits. Sur copie d'examen de quadrillage 5x5 mm, AB fera 26 carreaux tout comme CD et AD fera 3 carreaux tout comme BC. ::: 4. Les périmètres de ABCD et EFGH sont-ils égaux? :::success ::: spoiler ++Correction++ Périmète($rectangle$) = $2\times(L+l)$ Donc Périmètre(ABCD) = $2\times(AB+AD)$ Périmètre(ABCD) = $2\times(13+1,5)$ Périmètre(ABCD) = $2\times14,5$ soit **Périmètre(ABCD) = 29 cm**. or **Périmètre(EFGH) = 12 cm** d'après la question 1, donc <mark>les périmètres de ABCD et EFGH ne sont pas égaux</mark>. ::: ## Partie B Dans cette partie, on cherche pour quelle(s) valeur(s) de 𝑥 le périmètre du rectangle est égal au périmètre du carré. 1. Pour essayer de répondre au problème, on utilise la feuille de calcul suivante : | | A | B | C | D | E | F | G | |:-----:|:-------------------------:|:---:|:---:|:---:|:---:|:---:|:--- | | **1** | Valeur de 𝑥 | 1 | 2 | 3 | 4 | 5 | 6 | | **2** | Périmètre<br>du carré | 8 | 16 | 24 | 32 | 40 | 48 | | **3** | Périmètre du<br>rectangle | 30 | 28 | 26 | 24 | 22 | 20 | a) Quelle formule a-t-on pu saisir dans la cellule B2 avant de l’étirer jusqu’à G2? :::success ::: spoiler ++Correction++ B2 donne le périmètre du carré EFGH : la longueur du côté EF est donnée 2×B1 donc le périmètre fait 4×EF soit 8×B1. Donc en B2 on peut saisir <mark>= 8${}*{}$B1</mark>. *Remarque : on aurait pu saisir directement $=4 * 2 * B1$* ::: b) Ce tableau nous permet-il de trouver une valeur de 𝑥 pour laquelle les deux périmètres sont égaux? :::success ::: spoiler ++Correction++ *L'une ou l'autre ou les 2 réponses suivantes seraient acceptées.* - Dans une même colonne, on ne voit pas le même nombre en ligne 2 et en ligne donc <mark>on ne trouve pas cette valeur</mark> directement. - <mark>On peut encadrer cette valeur</mark> : les valeur de la ligne 2 augmentent de 8 à 48 quand les valeurs de la ligne 3 diminuent de 30 à 20; Mieux les 2 suites de valeurs se croisent donc au niveau des colonnes D et E : - ligne 2, le périmètre du carré augmente de 24 à 32, - ligne 3, le périmètre du rectangle diminue de 26 à 24. Donc <mark>la valeur de 𝑥 cherchée est entre 3 et 4</mark>. ::: 2. a) Montrer que le périmètre du rectangle peut s’écrire -2𝑥 + 32. :::success ::: spoiler ++Correction++ Dans la partie A, au 4., on a vu que Périmètre(ABCD)=$2\times(AB+AD)$. Or AB=16-2𝑥 et AD=𝑥 donc Périmètre(ABCD)= $2\times(16-2𝑥 ~+~𝑥)$ d'où Périmètre(ABCD)= $2\times(16-𝑥)$ En développant, Périmètre(ABCD)= $2\times16-2\times𝑥$ donc Périmètre(ABCD)= $32-2𝑥$ ainsi <mark>Périmètre(ABCD)= -2𝑥+32</mark>. ::: b) Déterminer la solution au problème par la résolution d’une équation. :::success ::: spoiler ++Correction++ Exprimons maintenant le périmètre du carré en fonction de 𝑥. Comme Périmète($carré$)=$4côté$, Périmètre(EFGH)= $4\times EF$ avec EF=2𝑥. Donc Périmètre(EFGH)= $4\times 2$𝑥. Ainsi Périmètre(EFGH)= 8𝑥. Donc les périmètres seront égaux quand -2𝑥+32=8𝑥, équation à résoudre : en ajoutant 2𝑥 dans les 2 membres on a 32=10𝑥. D'où 𝑥=$\dfrac{32}{10}$ Ainsi 𝑥=3,2. Ainsile périmètre du rectangle est égal au périmètre du carré pour <mark>une seule valeur 𝑥=3,2</mark>. *Remarque : la valeur est bien entre 3 et 4 comme estimé à la question 1.b).* ::: # Exercice 4 (17 points) Dans cet exercice, aucune justification n’est attendue. 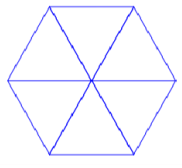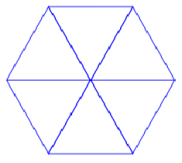Rappel : L’instruction <span style=" background:royalblue; color:white;">[s’orienter à 90]</span> signifie que le lutin se dirige vers la droite  ## Partie A Un élève souhaite tracer un hexagone à partir de 6 triangles équilatéraux comme sur la figure suivante :   | Pour cela, il commence par écrire le script ci-dessous du motif « triangle équilatéral ».   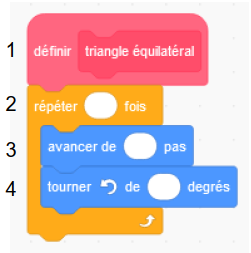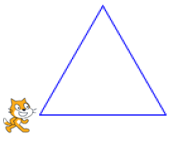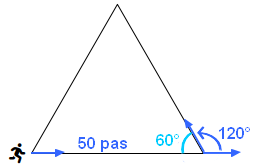1. Compléter et recopier sur la copie les lignes 2, 3 et 4 du script pour que le lutin dessine un triangle équilatéral de côté 50 pas. 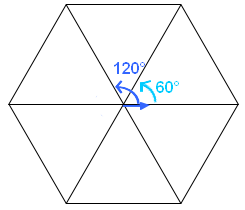:::success ::: spoiler ++Correction++ * <span style=" background:darkorange;color:white;">[répéter <mark>3</mark> fois]</span> * <span style=" background:royalblue; color:white;">[avancer de <mark>50</mark> pas]</span> * <span style=" background:royalblue; color:white;">[tourner Gauche de <mark>120</mark> degrés]</span> *La justification n'était pas demandée.* Les angles d'un triangle équilatéral font 60°. L'angle du <span style=" background:royalblue; color:white;">[tourner]</span> est 120° car, une fois arrivé à un sommet, le lutin tourne en regardant vers l'extérieur du triangle.  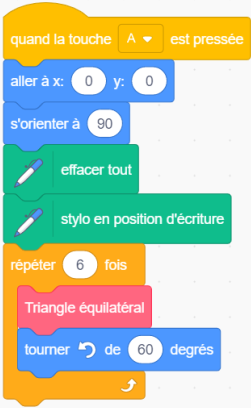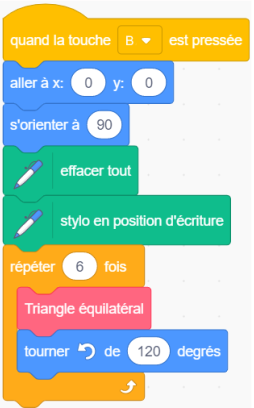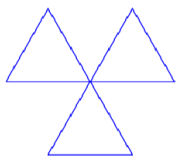::: 2. Cet élève teste les deux programmes A et B. Il obtient les deux dessins ci-dessous. Quel programme permet de tracer l’hexagone souhaité? **Programmes testés** | Programme A | Programme B | |:--------------------------------------------------------------------------------------:|:-------------------------------------------------------------------------------------- | |  |  | | Dessins obtenus | |:--------------------------------------------------------------------------------------:| |  | |  | :::success ::: spoiler ++Correction++ <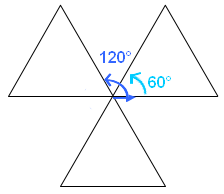mark>Le programme A permet d'obtenir l'hexagone</mark>. *La justification n'était pas demandée.* Une fois le 1er tirangle tracé par le bloc <span style=" background:deeppink; color:white;">[triangle équilatéral]</span> le lutin est revient à l'origine (0;0) et regarde à droite : il doit alors tourner de 60° vers la gauche pour repasser le côté gauche du triangle tracé puis le compléter ensuite à sa gauche. C'est donc le bloc <span style=" background:royalblue; color:white;">[tourner Gauche]</span> avec 60° et non 120° qui convient.   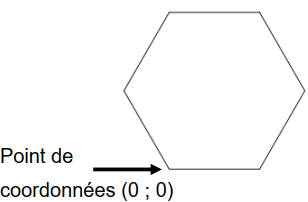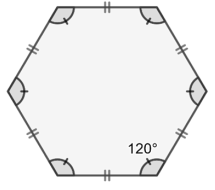:::success ::: ## Partie B Un autre élève souhaite tracer un hexagone régulier de 50 pas de côté comme sur la figure ci-dessous. 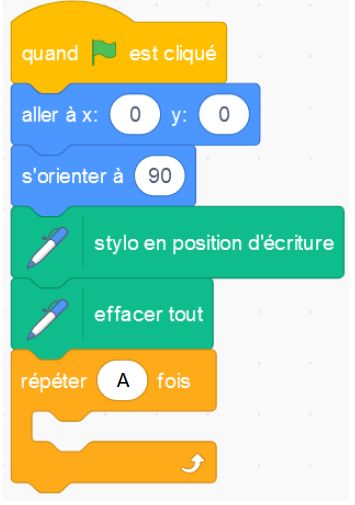| Figure obtenue | Informations sur les hexagones | |:--------------------------------------------------------------------------------------:|:--------------------------------------------------------------------------------------:| |  |  | Il a écrit le programme suivant :  Sur la copie, recopier le bloc « répéter » en remplaçant A par sa valeur et en le complétant avec 2 instructions choisies parmi les 6 instructions proposées ci-dessous.   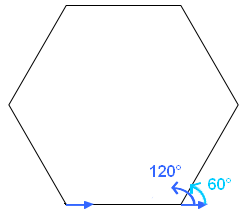:::success ::: spoiler ++Correction++ * <span style=" background:darkorange;color:white;">[répéter <mark>6</mark> fois]</span> * <span style=" background:royalblue; color:white;">[avancer de <mark>50</mark> pas]</span> * <span style=" background:royalblue; color:white;">[tourner Gauche de <mark>60</mark> degrés]</span> *La justification n'était pas demandée.* L'angle est 60° car, une fois arrivé à un sommet, le lutin tourne en regardant vers l'extérieur du triangle.  ::: # Exercice 5 (23 points) ## Partie A Un magasin a reçu 650 poissons dont 350 poissons de type A et 300 poissons de type B. Le responsable du magasin souhaite vendre ces poissons par lots de sorte que : * le nombre de poissons de type A soit le même dans chaque lot; * le nombre de poissons de type B soit le même dans chaque lot; * tous les poissons soient répartis dans les lots. 1. Parmi les trois propositions suivantes, laquelle correspond à la décomposition en produits de facteurs premiers du nombre 300? Aucune justification n’est demandée. | Proposition 1 | Proposition 2 | Proposition 3 | | ------------- | ------------- | ------------- | | $2^2\times 5\times15$ | $2\times 2\times 3\times 25$ | $2^2\times 3\times 5^2$ | :::success ::: spoiler ++Correction++ La <mark>proposition 3</mark> convient. *La justification n'était pas demandée.* Outre que le calcul fait bien 300, c'est la seule écriture avec des nombres premiers : dans les autres propositions, 15 et 25 ne sont pas premiers. ::: 2. Donner la décomposition en produit de facteurs premiers du nombre 350. :::success ::: spoiler ++Correction++ 350 = 2 × 175 350 = 2 × 5 × 35 350 = 2 × 5 × 5 × 7 donc <mark>350 = 2 × 5^2^ × 7</mark> *Remarque : "donner" sous-entend de ne pas justifier, mais la prudence est de mise.* ::: 3. Quel nombre maximal de lots, le responsable du magasin pourra-t-il constituer? Dans ce cas, combien y aura-t-il de poissons de chaque type dans chaque lot? :::success ::: spoiler ++Correction++ Pour faire le plus nombre de lots, il faut diviser 300 et 350 par le plus grand nombre entier possible qui donne un résultat entier : leur plus grand diviseur commun. Grâce aux 2 décompositions en facteurs premiers, 2×5^2^ est ce nombre; comme 2×5^2^=50, on a 300=50×6 et 350=50×7. Ainsi il y aura au maximum <mark>50 lots de 7 poissons de type A et 6 poissons de type B</mark>. ::: ## Partie B Le magasin a d’autres poissons, appelés « poissons combattants ». 1. En captivité, il faut prévoir au moins 15 litres d’eau pour un poisson combattant. Sachant qu’un aquarium se remplit au $\dfrac{4}{5}$ de sa hauteur, lequel doit-on choisir pour un poisson combattant? | Aquarium 1 | Aquarium 2 | 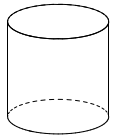|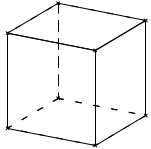:--------------------------------------------------------------------------------------:|:--------------------------------------------------------------------------------------:| |  |  | | Cylindre<br>Diamètre de la base : 30 cm<br>Hauteur : 25 cm | Pavé droit<br>Longueur : 28 cm<br>Largeur : 28 cm<br>Hauteur : 30 cm | | Rappels | |:----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------:| | Le volume d’un pavé droit est donné par la formule :<br>V = Longueur × Largeur × Hauteur<br>Le volume d’un cylindre de rayon de la base 𝑟 est donné par la formule :<br> V = π × 𝑟^2^× Hauteur | | 1 dm^3^ = 1 L | :::success ::: spoiler ++Correction++ 15 L = 15 dm^3^ = 15 000 cm^3^. - ++Aquarium 1++ : Volume(Cylindre). = π × 𝑟^2^× Hauteur = π × 15^2^× 25 car 30÷2=15 ≈ 17 729,44 cm^3^ $\dfrac{4}{5} \times 17 729,44 \approx 14 183,55$ donc l'aquarium 1 contient 14 183,55 cm^3^ d'eau environ, soit environ 14,2 dm^3^. Ce n'est pas suffisant. - ++Aquarium 2++ : Volume(Pavé) = Longueur × Largeur × Hauteur = 28 × 28 × 30 = 23 520 cm^3^ $\dfrac{4}{5} \times 23 520 = 18 816$ donc l'aquarium 2 contient 18 816 cm^3^ d'eau, soit 18 L. C'est suffisant. Pour un poisson combattant il faut choisir <mark>l'aquarium 2</mark>. *Remarque : une fois l'aquarium 1 éliminé on pouvait conlure car la question sous-entendait qu'un des 2 convenait. Mais la prudence est de mise.* ::: 2. Le prix d’un poisson combattant est de 15 €. Une famille achète un poisson combattant et un aquarium. L’aquarium coûte 40 €. Le vendeur fait une réduction de 15 % sur le prix total. Combien va payer la famille? :::success ::: spoiler ++Correction++ 15 + 40 = 55 donc le poisson avec l'aquarium coûtent 55 €. 15 % de ces 55 € font 8,25 € car $\dfrac{15}{100}\times55$=8,25. 55-8,25 = 46,75 donc la famille va payer <mark>46,75 €</mark>. :::