# BEZIER
## barycentre, matrice , fonction, combinatoire & co

---
# barycentre
## MOYENNE PONDEREE
## CENTRE DE GRAVITE
----
Le barycentre des points A et B affectés des masses a et b (a + b non nul) est l'unique point G tel que
$a\vec{GA}+b\vec{GB}=\vec{0}$
Les coordonnées de G sont alors
$x_G=\frac{ax_A+bx_B}{a+b}$ $y_G=\frac{ay_A+by_B}{a+b}$ $z_G=\frac{az_A+bz_B}{a+b}$
----
Le nombre de points peut passer à trois points, quatre points et se généraliser à n points. Si la somme des masses ai est non nulle, le barycentre du système ${(Ai, ai )}_i ∈ \{1 ; n \}$ est le point G tel que :-1:
$\sum_{i=1}^na_i\vec{GA_i}=\vec{0}$
----
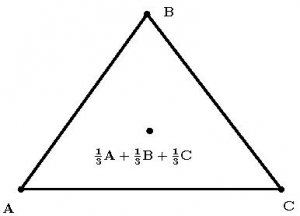
Ainsi, le centre de gravité du triangle est exactement l'isobarycentre des sommets du triangle, c'est-à-dire que
${\displaystyle {\overrightarrow {GA}}+{\overrightarrow {GB}}+{\overrightarrow {GC}}={\overrightarrow {0}}.}$
----

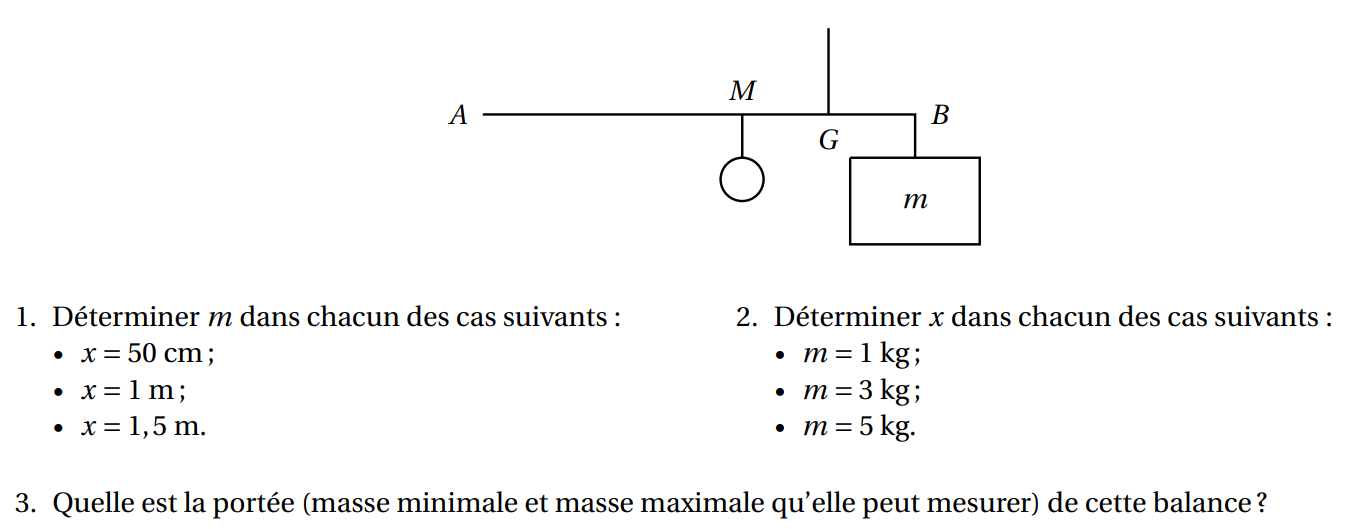
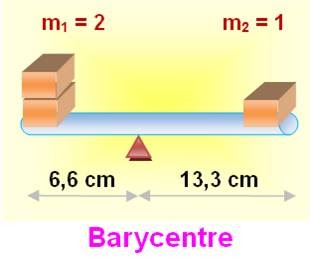
1. Déterminer la position du point d’équilibre dans les cas suivants :
• m = 1 et m′ = 1 ; • m = 2 et m′ = 1 ; • m = 3 et m′ = 5
----
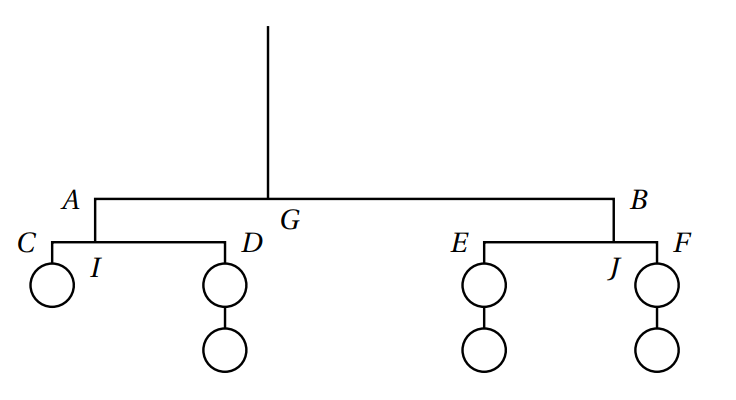
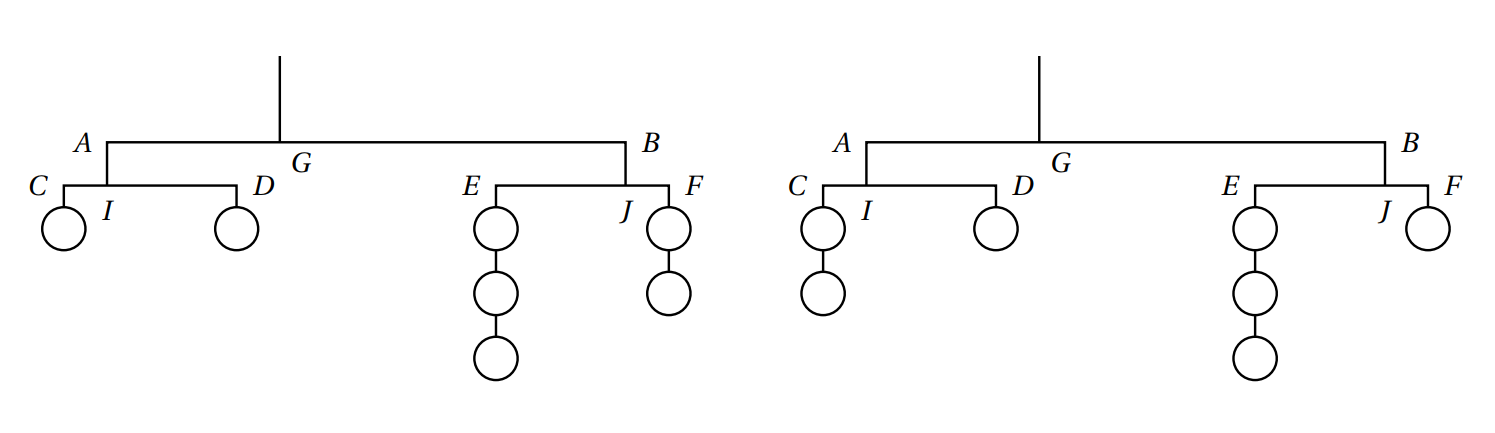
Le mobile du schéma suivant est formé de tiges et de fils de masses négligeables tel que AB = 30 cm et CD = EF = 10 cm et de sept billes de 10 g chacune. Il est en équilibre.
Déterminer les positions exactes de I, J et G.
----
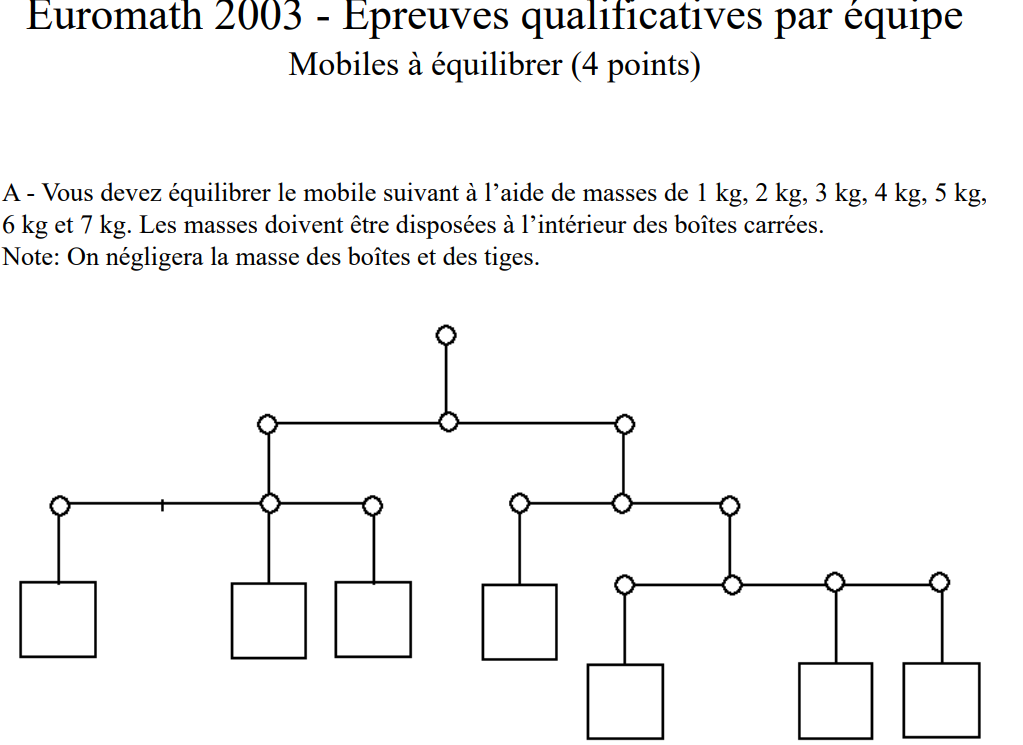
https://www.maths-pour-tous.org/cours-mej/doc/sujets2019/equilibre/euromath.pdf
----
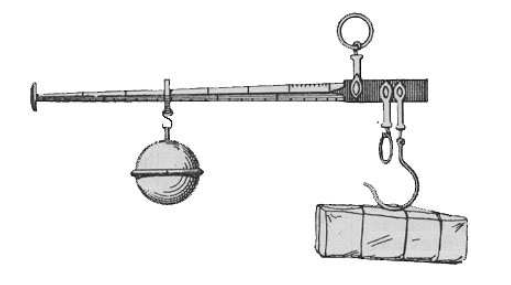
#### Balance romaine
Contrairement à une balance classique, dans une balance romaine, les deux bras du fléau n’ont pas la même longueur.
Le bras du côté de la masse inconnue a une longueur constante alors que la longueur du bras qui supporte le contre-poids est variable
----
Même question avec les mobiles du schéma 3 page suivante.
----
- Dans cette balance, on n’obtient pas l’équilibre en égalisant les deux masses, mais en agissant sur la longueur du bras qui porte le contre-poids.
- L’équilibre se fait lorsqu’en déplaçant ce contre-poids le long de sa tige, le fléau atteint la position horizontale.
- Le bras le plus long porte des divisions avec indication des poids correspondants.
- Il suffit alors de lire le poids de l’objet.
- Il faut noter que la différence de longueur entre les bras permet de peser des charges beaucoup plus importantes que celle du contre-poids.
----
Pour cette activité on modélisera une balance romaine de la façon suivante :
• la balance est constituée d’une tige AB indéformable et de masse négligeable telle que AB = 2,5 m ;
• la balance est fixée au plafond en G, tel que BG = 0,5 m ;
• la masse inconnue m est fixée au bout d’un crochet de masse négligeable fixé en B ;
• un contre-poids de deux kilogrammes est fixé en M au bout d’un crochet de masse négligeable, tel que M ∈ [AB]. On note x = MG.
----
----
https://images.math.cnrs.fr/Mobiles-de-Calder

----
Interaction: https://homeomath2.imingo.net/bary1.htm
https://www.geogebra.org/m/b3ku3uzp
----
https://images.math.cnrs.fr/Une-tour-de-cartes-qui-penche-a-l-infini

----
https://images.math.cnrs.fr/Le-logo-du-CNRS.html
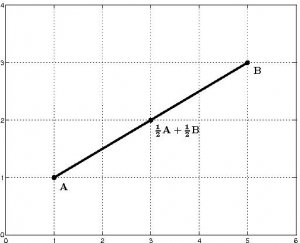
A (1,1) et B(5,3), alors le milieu du segment AB a pour coordonnées (1+52,1+32)=(3,2).
On note souvent ce milieu comme une moyenne des deux points : $\frac{1}{2}A+\frac{1}{2}B$
----
https://images.math.cnrs.fr/Poids-poulies-et-point-de-Fermat-Steiner.html

----
<iframe width="100%" height="500"
src="https://www.geogebra.org/m/r9JpfesY#material/P8HwSFAk" sandbox>
</iframe>
----
----
----
https://chingmath.fr/hp-lycee/barycentres/ressources
<iframe width="100%" height="500"
src="https://chingmath.fr/ress595-0-1.pdf" sandbox>
</iframe>
---
# barycentres
des exos
----
https://chingmath.fr/hp-lycee/barycentres.pdf
<iframe width="100%" height="500"
src="https://chingmath.fr/hp-lycee/barycentres.pdf" sandbox>
</iframe>
----

----
---
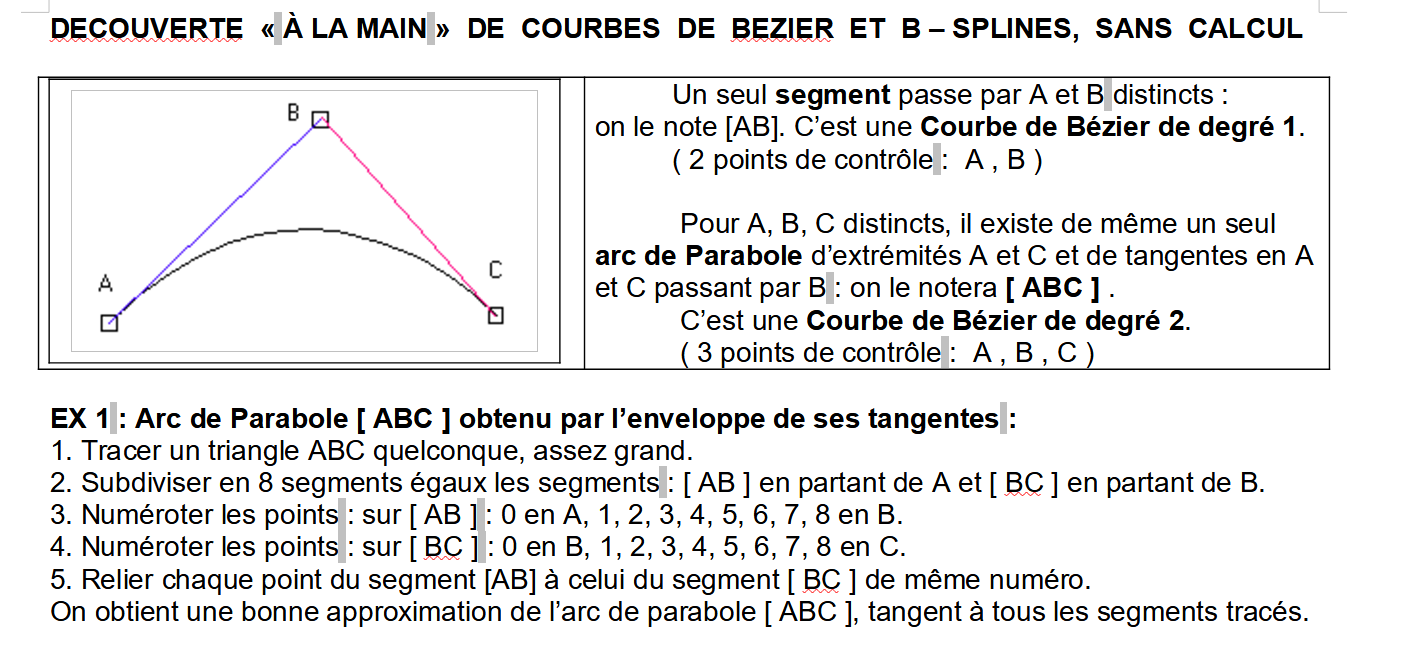
# courbe de BEZIER
constructions
----
----

----

----
1
<iframe width="100%" height="500"
src=" https://www.geogebra.org/m/nkqs3rbs" sandbox>
</iframe>
----
2
<iframe width="100%" height="500"
src=" https://www.geogebra.org/m/JPNHEgmh " sandbox>
</iframe>
---
# courbe de Bézier
[wikipedia](https://www.wikiwand.com/fr/Courbe_de_B%C3%A9zier#Applications)
## videos
----
{%youtube 2pNjW-2944Y %}
----
{%youtube Hm-HO-HtVYo %}
----
{%youtube _Z07z13Tol4 %}
----
{%youtube IUQwQdabhNM %}
----
{%youtube aVwxzDHniEw %}
----
{%youtube jvPPXbo87ds %}
----
---
# animations
----

----
<iframe width="100%" height="500"
src="https://www.jasondavies.com/animated-bezier/" >
</iframe>
----
[](https://www.vous-et-nous.eu/uploads/exercices/svg/bezier.svg )
---
# histoire
----
[]( http://www.mathom.fr/sites/default/files/ADS/Bezier.pdf#page=7)
----
<iframe width="100%" height="500"
src="https://laforetdessciences.wordpress.com/2019/03/21/les-belles-carrosseries/" >
</iframe>
----
[](https://citeseerx.ist.psu.edu/pdf/1f4d1ef865272e3976539e61bb184adca4f4525a)
---
# aspect polynome
----
<iframe width="100%" height="500"
src="https://pomax.github.io/BezierInfo-2/#explanation" >
</iframe>
[en français](https://pomax-github-io.translate.goog/bezierinfo/?_x_tr_sl=auto&_x_tr_tl=fr&_x_tr_hl=fr&_x_tr_pto=wapp#explanation)
----
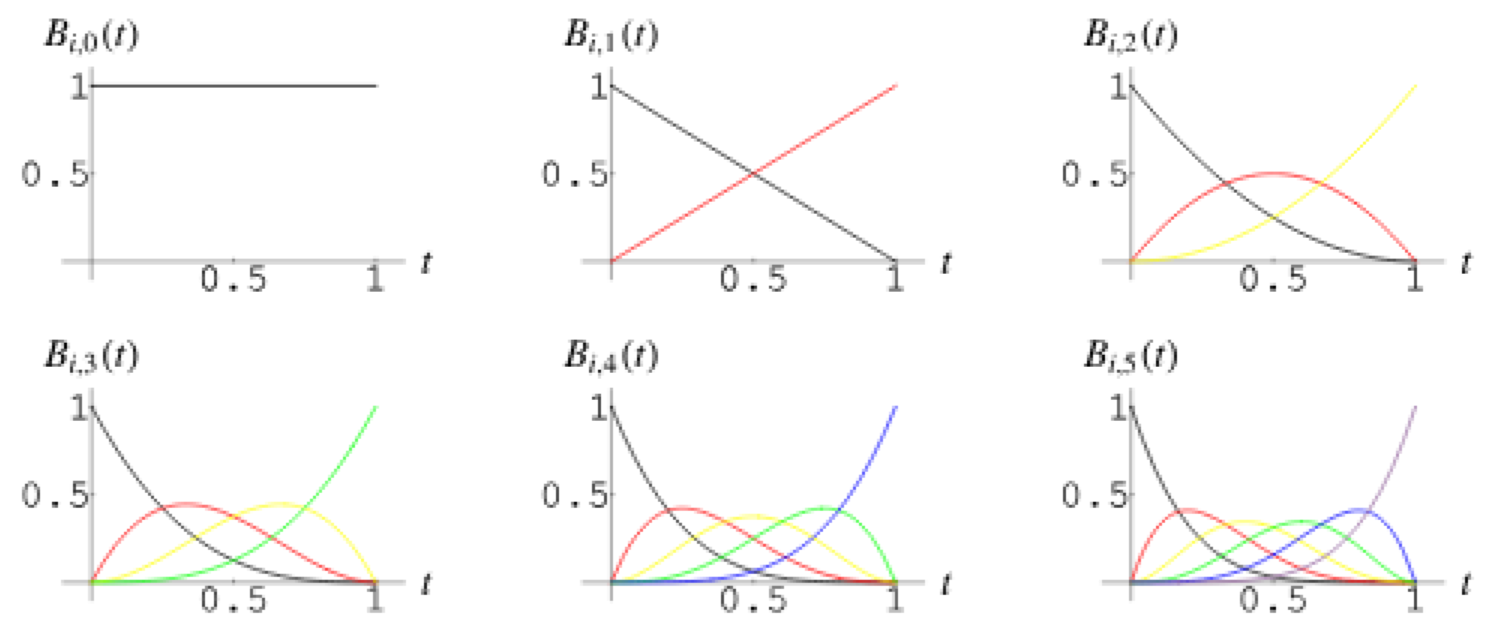
$(t + (1 - t))^n = 1$ et $$(a+b)^n = \sum_{k=0}^n{n\choose k} \cdot a^kb^{n-k}$$(Newton)
----
donne
$$(t+(1-t))^n = \sum_{k=0}^n{n\choose k} \cdot t^k(1-t)^{n-k}$$
avec $B_k^n ( t) = {n\choose k} \cdot t^k(1-t)^{n-k}$, $k \in \{0,...,n\}$
polynome de Bernstein, avec ${n\choose k}=\frac{n!}{k!(n-k)!}$
----
## cas n=1
$B_k^1 ( t) = {1\choose k} \cdot t^k(1-t)^{1-k}$
- $B_0^1 ( t) = {1\choose 0} \cdot t^0(1-t)^{1-0}=1-t$
- $B_1^1 ( t) = {1\choose 1} \cdot t^1(1-t)^{1-1}=t$
----
## cas n=2
$B_k^2 ( t) = {2\choose k} \cdot t^k(1-t)^{2-k}$
- $B_0^2 ( t) = {2\choose 0} \cdot t^0(1-t)^{2-O}=(1-t)^2$
- $B_1^2 ( t) = {2\choose 1} \cdot t^1(1-t)^{2-1}=2t(1-t)$
- $B_2^2 ( t) = {2\choose 2} \cdot t^2(1-t)^{2-2}=t^2$
----
----
Etant donné n+1 points (P0, …, Pn)appelés points de controle, la courbe de Bézier définit par ces points est :
$$P(t)=\sum_{k=0}^nB_k^n ( t)\cdot P_k$$ avec $0\leq t \leq1$
----
**cas n=1**
$P(t)=B_0^1 ( t)\cdot P_0+B_1^1 ( t)\cdot P_1=(1-t)P_0+tP_1$
P se balade entre $P_0$ et $P_1$
----
**cas n=2**
$P(t)=B_0^2 ( t)\cdot P_0+B_1^2 ( t)\cdot P_1+B_2^2 ( t)\cdot P_2$
$P(t)=(1-t)^2P_0+2t(1-t)P_1+t^2P_2$
P se passe par $P_0$ et $P_1$ , pas par $P_2$
---
# aspect matrice
----
<iframe width="100%" height="500"
src="https://pomax.github.io/BezierInfo-2/#matrix" >
</iframe>
https://pomax-github-io.translate.goog/bezierinfo/?_x_tr_sl=auto&_x_tr_tl=fr&_x_tr_hl=fr&_x_tr_pto=wapp#matrix
----
<iframe width="100%" height="500"
src="https://www.geogebra.org/classic/bj4fhwn8" >
</iframe>
---
# avec python
----
https://download.tuxfamily.org/tehessinmath/les%20pdf/JA2015Bezier.pdf

---
# à voir
----
## courbes et surfaces
[]( https://ciechanow-ski.translate.goog/curves-and-surfaces/?_x_tr_sl=auto&_x_tr_tl=fr&_x_tr_hl=fr&_x_tr_pto=wapp
)
---
## des tps
----
http://math.teulie.free.fr/documents/btscrsa2/tp_info/tp_08_geogebra.pdf

---
## concours général
https://euler.ac-versailles.fr/IMG/pdf/cg_s_2018.pdf
<iframe width="100%" height="500"
src=" https://euler.ac-versailles.fr/IMG/pdf/cg_s_2018.pdf#page=2 " sandbox></iframe>
----
https://euler.ac-versailles.fr/IMG/pdf/cg_2018_correction_s.pdf
<iframe width="100%" height="500"
src=" https://euler.ac-versailles.fr/IMG/pdf/cg_2018_correction_s.pdf " sandbox></iframe>
---
# svg
----
https://svg-path-visualizer.netlify.app/#M%2030%2075%20Q%20240%2030%2C%20300%20120
<iframe width="100%" height="500"
src="https://svg-path-visualizer.netlify.app/#M2%2C2%20Q8%2C3%2010%2C8" sandbox></iframe>
----
<iframe src="https://trinket.io/embed/html/5cd2750f99" width="100%" height="600" frameborder="0" marginwidth="0" marginheight="0" allowfullscreen></iframe>
----
https://lyceealaincolas.fr/wp-content/uploads/2022/09/maths-dnm-SVG.pdf
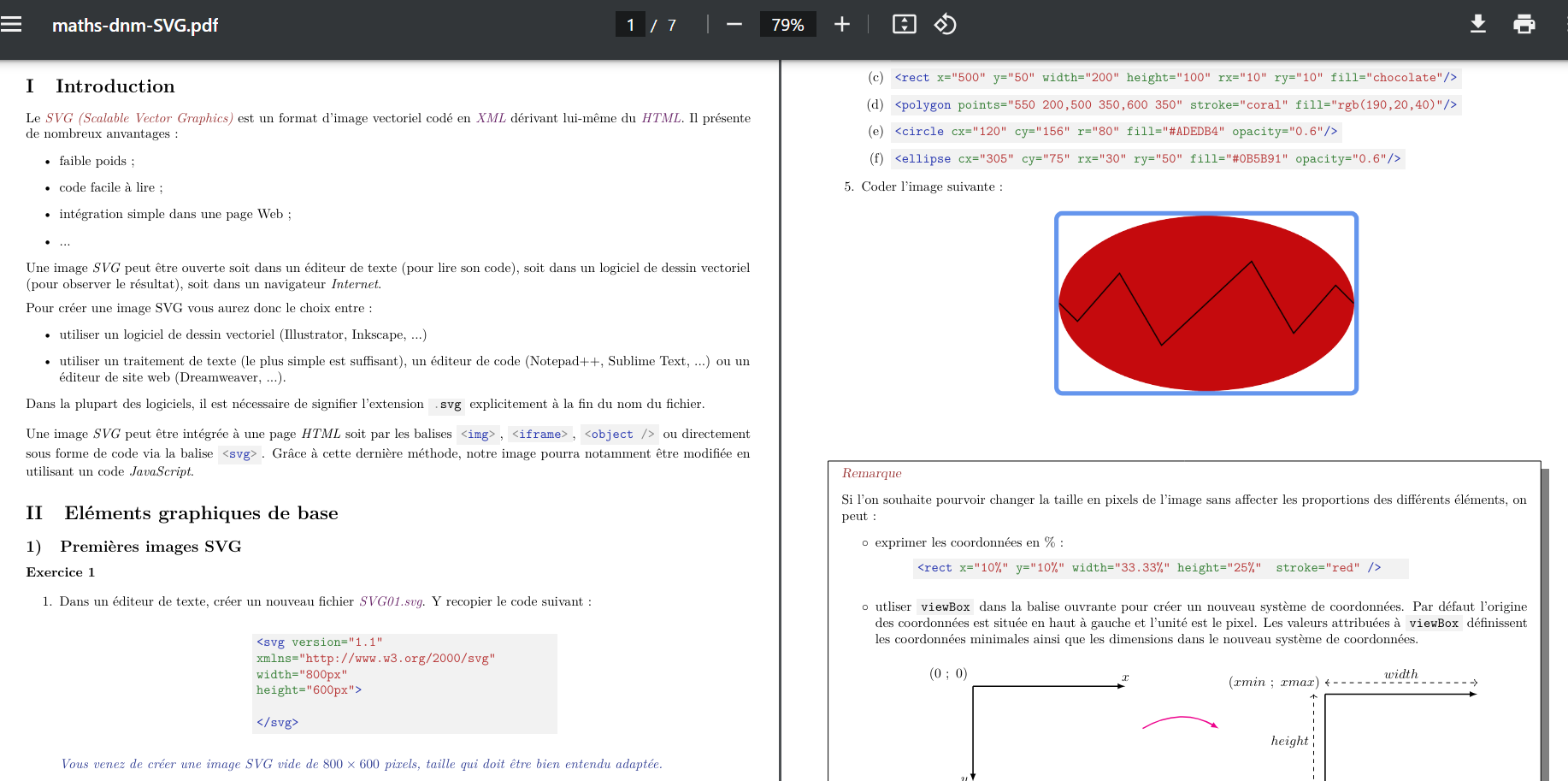
----
https://fr.javascript.info/bezier-curve
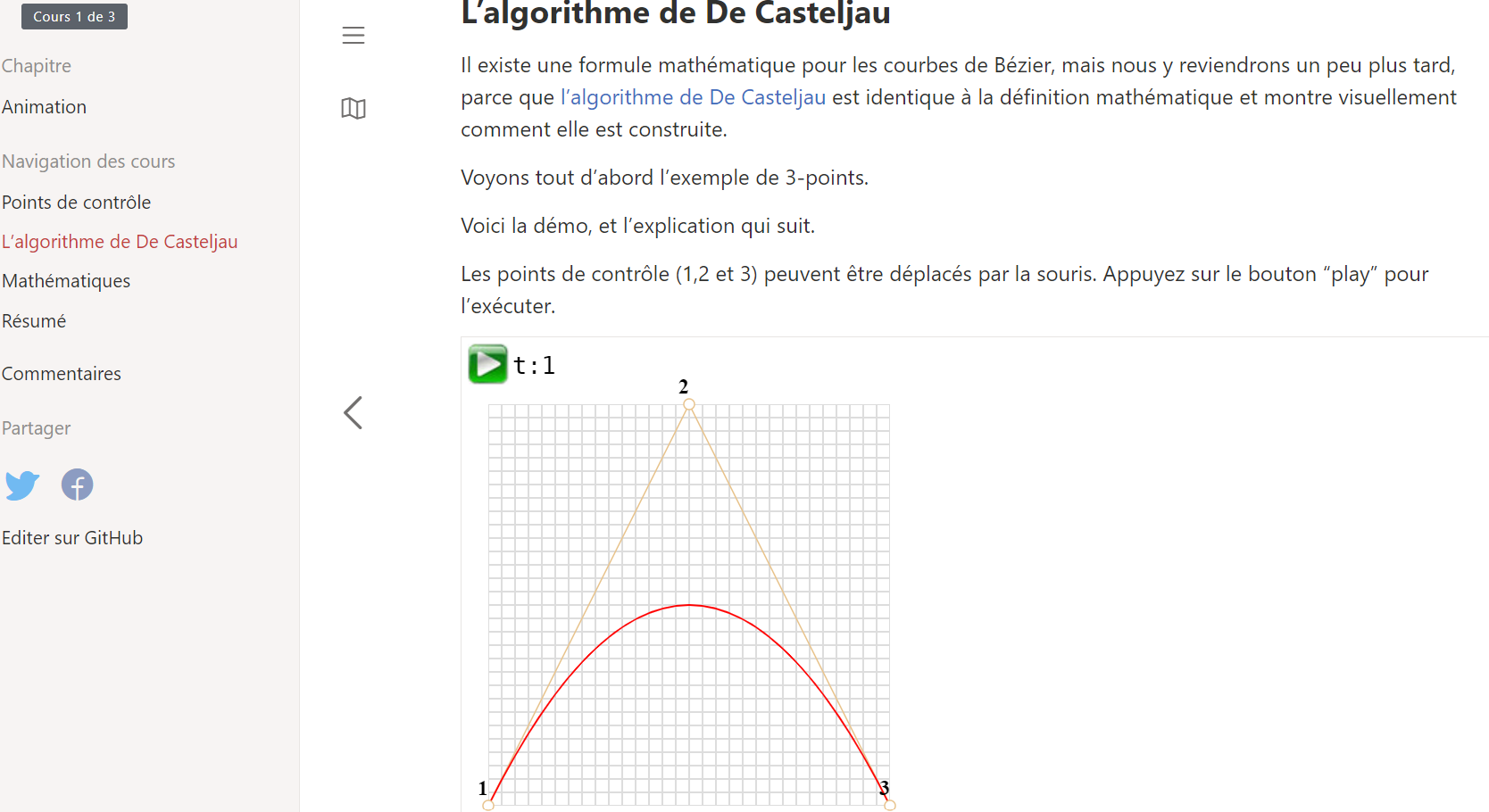
----
https://math.univ-lyon1.fr/irem/Formation_ISN/formation_svg/path/path.html

----
http://mathartung.xyz/siteICN/svg_a1.html
----
http://uncledens.chez-alice.fr/divers/hexagone/index.htm
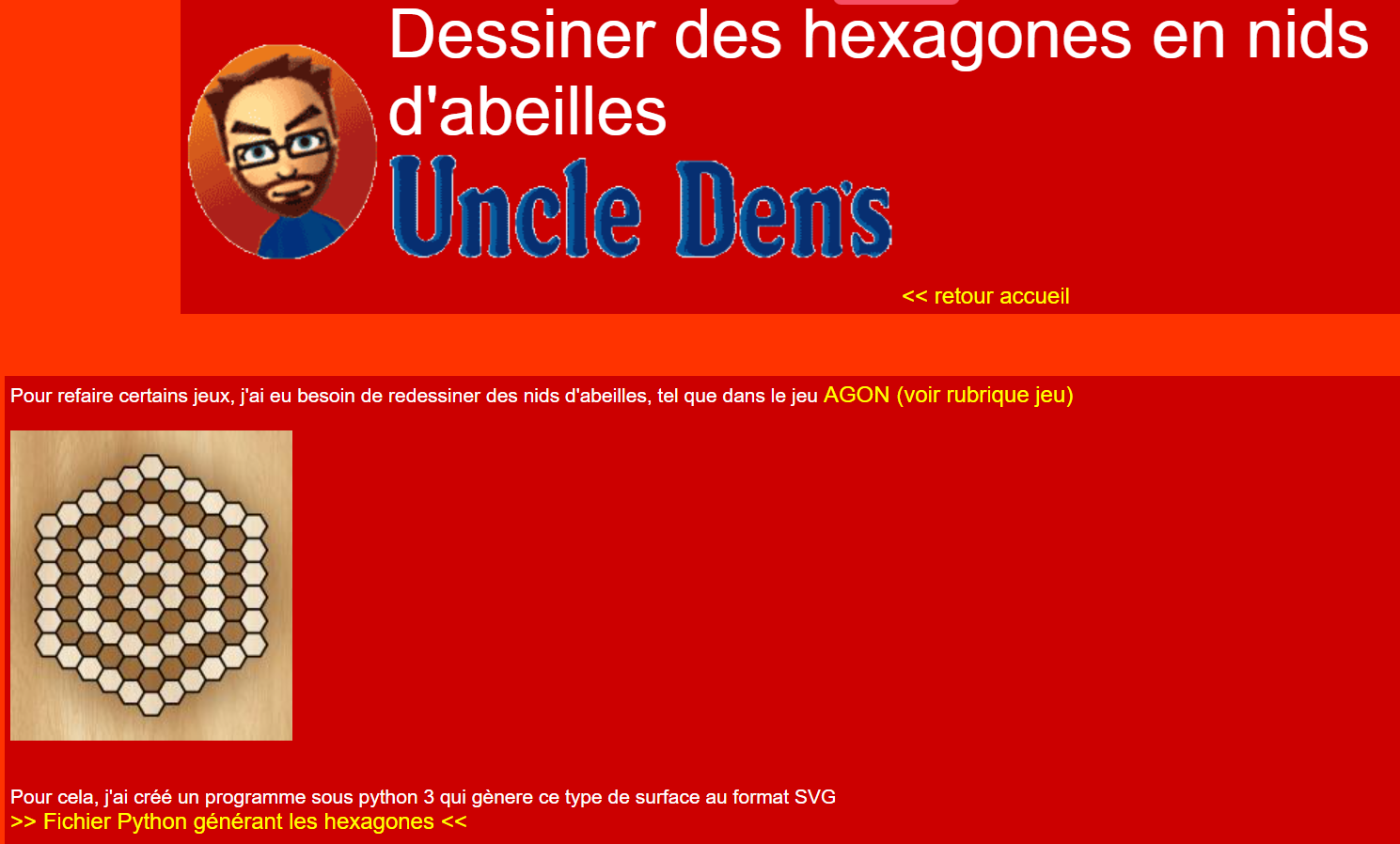
----
http://uncledens.chez-alice.fr/divers/drapeau/drapeau.htm

----
https://www.darchevillepatrick.info/svg/svg1.php#corps
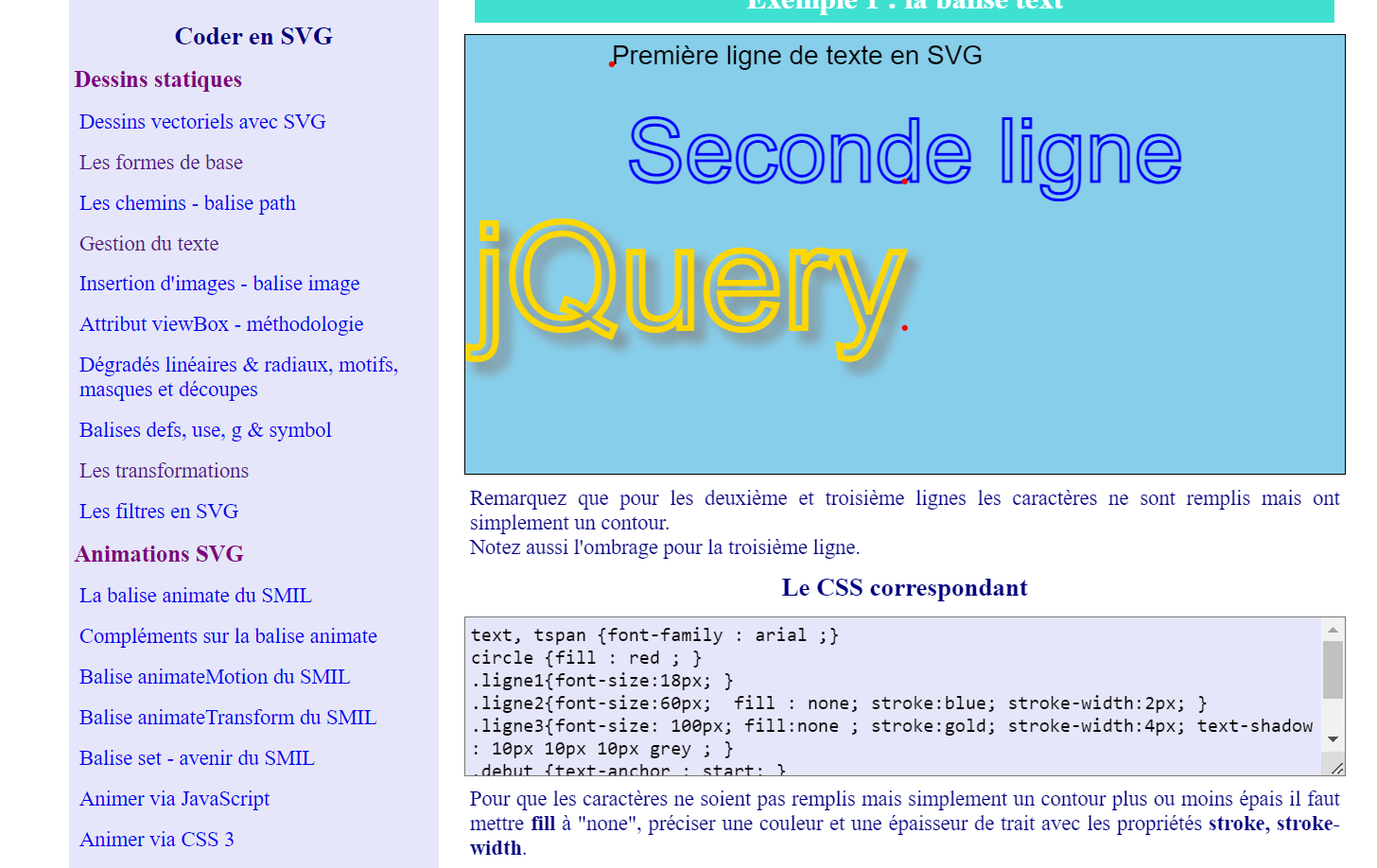
----
**Stage MathC2+**
[Activité autour du dessin vectoriel et des Sangaku](https://irem.univ-grenoble-alpes.fr/medias/fichier/fichierseleves2017_1558356936676-zip?ID_FICHE=106201&INLINE=FALSE)
---
https://accromath.uqam.ca/wp-content/uploads/2017/09/Typographie.pdf

---
https://www-irem.univ-paris13.fr/site_spip/IMG/pdf/brochure_numero_47_-_courbes_de_bezier_et_b._splines.pdf
<iframe width="100%" height="100%"
src=" https://www-irem.univ-paris13.fr/site_spip/IMG/pdf/brochure_numero_47_-_courbes_de_bezier_et_b._splines.pdf " sandbox></iframe>
---
http://www.christianboyer.com/jumieges/rabutcolloquebezier.pdf
http://docs.les-renault-d-avant-guerre.com/Section_d_Histoire_des_Usines_Renault.pdf
http://www.sens-neuchatel.ch/bulletin/no34/art3-34.pdf
---
[La vie de De Casteljau](
https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4497291)
---
<div style="text-align:center;"><div style="margin:8px 0px 4px;"><a href="https://www.calameo.com/books/0065226585d511881a2d2" target="_blank">2008 04 Bezier</a></div><iframe src="//v.calameo.com/?bkcode=0065226585d511881a2d2&mode=mini" width="480" height="600" frameborder="0" scrolling="no" allowtransparency allowfullscreen style="margin:0 auto;"></iframe><div style="margin:4px 0px 8px;"><a href="http://www.calameo.com/" target="_blank">Lire plus de publications sur Calaméo</a></div></div>
---
Spline
<iframe width="100%" height="500"
src="https://forum-labomaths.site.ac-lille.fr/wp-content/uploads/sites/64/2024/07/COURBES-DE-BEZIERS.pdf" >
</iframe>
---
[]( http://lyceeenligne.free.fr/IMG/pdf/Bspline-Cours.pdf)
---
Représentation des courbes et des surfaces
https://nuage03.apps.education.fr/index.php/s/K3rq3BzcP2akYZP
---
FicheScientifiqueBezier
https://sancy.iut.uca.fr/~iso/docs/bezier/FicheScientifiqueBezier.pdf
https://sancy.iut.uca.fr/~iso/docs/bezier/
https://sancy.iut.uca.fr/~iso/bezier/generator
---
en 3d
<div class="colum">
<div >
a = lerp( p[0], p[1], t )
b = lerp( p[1], p[2], t )
c = lerp( p[2], p[3], t )
d = lerp( a, b, t )
e = lerp( b, c, t )
point = lerp( d, e, t )
</div ><div >
<iframe width="100%" height="100%"
src="https://video.twimg.com/tweet_video/ER-Vyg6XkAEgrup.mp4" sandbox></iframe>
</div >
</div >
{"type":"slide","tags":"bezier, svg","title":"Bezier","autoSlide":10,"slideOptions":{"defaultTiming":20,"transition":"slide","progress":true,"parallaxBackgroundImage":"https://minio.apps.education.fr/codimd-prod/uploads/upload_c6279aa629a6bf4c65c455cb593234d1.jpg"}}