Cercles dans cercle === # l'idée de départ, un tweet Remplir un cercle d'une infinité de cercles tangents ---  https://twitter.com/i/status/1256824725814120448 <iframe src="https://video.twimg.com/ext_tw_video/1256824056944357376/pu/vid/320x320/DPioJgeHnW2Bk2JD.mp4?tag=10" > </iframe> --- # la construction Pour cela, on va s'appuyer sur les complexes. ## la partie haute - ### la ligne horizontale On a une droite d'équation y=1. 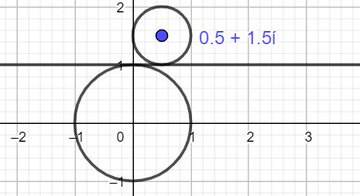On a la représente par a+i avec $a \in \mathbb{R}$ ---  --- - ### un cercle --le cercle trigo il est représenté par $e^{i \theta }$ avec $\theta \in \mathbb{R}$ -- un des petits cercles le premier auquel on s'intéresse a pour centre A tq $z_A=0,5+1,5i$ et pour rayon 0,5 Il s'obtient comme réduction d'un facteur 1/2 puis translation de vecteur $z_{ \vec{OA}}$ à partir du cercle trigo. 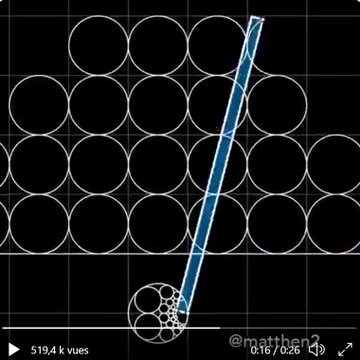il est ainsi représenté par $0,5e^{i \theta }+0,5+1,5i$ avec $\theta \in \mathbb{R}$ --- ::: spoiler concrètement avec Geogebra, on tulise un curseur pour l'angle et on active la trace 0.5+1.5 ί+0.5 ℯ^(ί α) ::: ggb| ce qu'on veut - | - |  --- - ### des cercles Tous les autres petits cercles sont obtenus par translation de vecteur $\vec{u}$ d'affixe $z_{\vec{u}}=m+ni$ avec $m \in \mathbb{N}$ et $n \in \mathbb{N^*}$ Ils sont ainsi représenté par $0,5e^{i \theta }+0,5+1,5i+m+ni$ avec $\theta \in \mathbb{R}$,$m \in \mathbb{N}$ et $n \in \mathbb{N^*}$ ---  --- ::: spoiler curseurs $\alpha$, m, n 0.5+1.5 ί+0.5 ℯ^(ί α)+n+ί m ::: ___ ## la transformation  --- 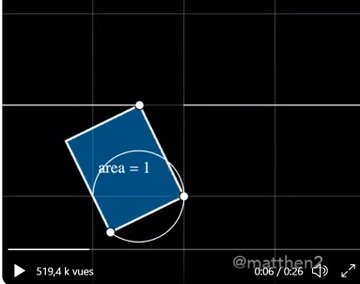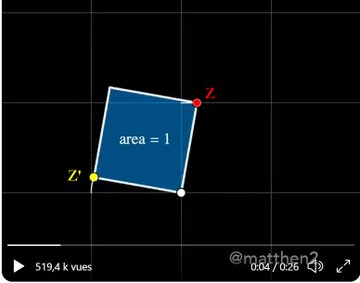Soit P le point dont l'affixe Z parcoura la droite et les petits cercles précédents et P' son image d'affixe Z' par la transformation qui conserve un rectangle d'aire 1 et telle que $(\vec{OP},\vec{OP'})=\pi/2$. On a ainsi les relations suivantes :::warning aire=1 : $|Z|*|Z'|=1$ angle droit arg($z_{\vec{OP}},z_{\vec{OP'}}$)=arg($\frac{Z'}{Z}$)=$\pi/2$ ::: On en déduit le module et l'argument de Z': $$ |Z'|=1/|Z|\\ arg(Z')=arg(Z)+\pi/2$$ --- Et comme $Z'=|Z'|e^{i arg(Z')}$ On obtient finalement :::warning $$Z'=\frac{1}{|Z|}e^{i (arg(Z)+\pi/2})$$ ::: :::spoiler en géogébra $(1)/(abs(z_{1})) ℯ^(ί ((π)/(2)+arg(z_{1})))$ ::: --- ## une ébauche de construction avec Geogebra --- <iframe src="https://www.geogebra.org/classic/twqwkatz" height="600" width="1000"> </iframe> --- ## un début de justification ### de la ligne vers le grand cercle On conjecture que la ligne est transformé en cercle C($\Omega$ =-0,5, R=0,5) On part d'un point Z=a+i $|Z|=\sqrt{a²+1}$, $arg(Z)=arctan(1/a)$ On veut montrer que $|Z'-(-0,5)|=|Z'+0,5|=0,5$ $|Z'+0,5|=| \frac{1}{|Z|}*e^{i (arg(Z)+\pi/2})+0,5|$ $|Z'+0,5|=|\frac{1}{\sqrt{a²+1}}e^{i (arctan(1/a)+\pi/2})+0,5|$ $|Z'+0,5|=|\frac{i}{\sqrt{a²+1}}e^{i (arctan(1/a)})+0,5$| --- $|Z'+0,5|=|\frac{i}{\sqrt{a²+1}}*(cos(arctan(1/a))+isin(arctan(1/a))+0,5|$ (magie?[^1] ) $|Z'+0,5|=|\frac{i}{\sqrt{a²+1}}*(\frac{a}{\sqrt{a²+1}}+i*\frac{1}{\sqrt{a²+1}})+0,5|$ $|Z'+0,5|=|\frac{-1+ia}{a²+1}+0,5|=|\frac{-1+0,5(a²+1)+ia}{a²+1}|=|\frac{0,5(a²-1)+ia}{a²+1}|$ $|Z'+0,5|=\frac{|0,5(a²-1)+ia|}{|a²+1|}=\frac{\sqrt{0,25(a²-1)²+a²}}{a²+1}=\frac{\sqrt{0,25a^4-0,5a²+0,25+a²}}{a²+1}$ $|Z'+0,5|=\frac{\sqrt{0,25a^4-0,5a²+0,25+a²}}{a²+1}=\frac{\sqrt{0,25a^4+0,5a²+0,25}}{a²+1}=\frac{\sqrt{0,25(a^4+2a²+1)}}{a²+1}$ $|Z'+0,5|=\frac{\sqrt{0,25(a^2+1)²}}{a²+1}=\frac{\sqrt{0,25}\sqrt{(a^2+1)²}}{a²+1}=0,5$ CQFD :::spoiler pseudo-vérif https://www.geogebra.org/classic/twfjtjrw ::: --- ### d'un cercle vers un autre cercle dans le grand cercle laissé au lecteur [^1]: magie ? on pose y=arctanx et le calcul est évident, je le détaille y=arctan x→ $x=tany=\frac{sin y}{cos y}$ → $x²+1=\frac{sin²y}{cos²y}+1=\frac{sin²y+cos²y}{cos²y}=\frac{1}{cos²y}$ D'où $cos(y)=cos(atanx)=\frac{1}{\sqrt{1+x²}}$ De même $sin(atanx)=\frac{x}{\sqrt{1+x²}}$