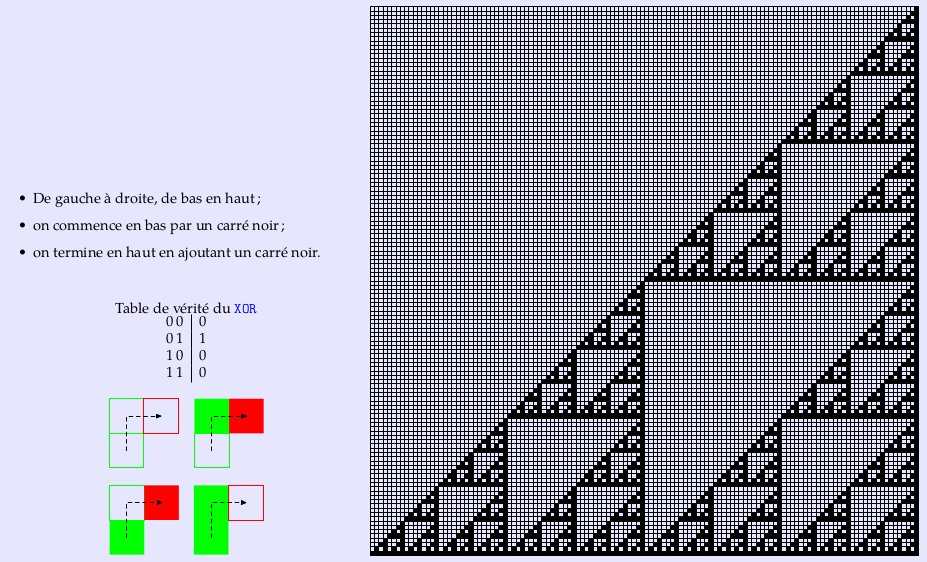
# 2024 # centenaire # MANDELBROT ## Fractales : constructions --- # fractale  --- Au menu: - construction géométriques(itérative et récursive) - L-systèmes - hasard - IFS - Lichtenberg: allumer le feu --- # construction géométriques(itérative et récursive) ---- Les algorithmes que nous allons considérer vont permettre de construire les étapes menant à une fractale jusqu’à un certain rang n . On peut distinguer deux types d’algorithmes : **les algorithmes itératifs et les algorithmes récursifs**: – Dans la démarche itérative, on passe de l’étape 1 à l’étape n à l’aide d’une boucle « pour » ; c’est-à-dire que l’on part de l’étape 1 (connue), on passe de 1 à 2, puis de 2 à 3, …, de n - 1 à n, on s’arrête à l’étape n souhaitée. – Dans la démarche récursive, on part de l’étape n (inconnue). Cette étape n’est pas connue, mais on la décrit en fonction de l’étape n - 1, qui elle-même est décrite en fonction de l’étape n - 2 et ainsi de suite jusqu’à arriver à l’étape 1 connue. On parvient au résultat voulu en écrivant un algorithme qui s’appelle lui-même. ---- https://www.apmep.fr/IMG/pdf/AAA12003.pdf https://www.thingiverse.com/thing:3156581 ----  --- https://e-nsi.forge.aeif.fr/recursif/4-Fractal/4-fractales_1/1-carres_1/ <iframe width="100%" height="500" src="https://e-nsi.forge.aeif.fr/recursif/4-Fractal/4-fractales_1/1-carres_1/ " > </iframe> --- <iframe width="100%" height="400" src="https://esperluet.wordpress.com/2016/03/07/generation-darbres-fractals/" sandbox> </iframe> </iframe> ----  ---- https://video.twimg.com/ext_tw_video/1321142357904007172/pu/vid/480x270/co7HfotlkOdiLlsF.mp4  ---- http://recursivedrawing.com/draw.html <iframe width="100%" height="500" src="https://player.vimeo.com/video/41822151?title=0&byline=0&portrait=0&color=cc0000" > </iframe> ---- https://sorciersdesalem.math.cnrs.fr/ArbrePythagore/arbre_pythagore.html <iframe width="100%" height="500" src="https://sorciersdesalem.math.cnrs.fr/ArbrePythagore/arbre_pythagore.html " sandbox></iframe> ---- https://mathsmagiques.fr/pages/truc_mat/textes/fractales.htm https://paestel.fr/sites/default/files/Mat_les_ressources/1%C3%A8re/Atelier%2C%20probl%C3%A8me/mlr-une_introduction_aux_fractales.pdf --- # L-systèmes ---- http://accromath.uqam.ca/2013/09/l-systemes-les-equations-des-plantes/ ---- [](http://www.kevs3d.co.uk/dev/lsystems/) ---- <iframe width="100%" height="500" src=" https://anvaka.github.io/lsystem/?code=axiom%3A%20X%0Arules%3A%20%0A%20%20X%20%3D%3E%20-YF%2BXFX%2BFY-%0A%20%20Y%20%3D%3E%20%2BXF-YFY-FX%2B%0A%0Adepth%3A%205%0AstepsPerFrame%3A%2010%0Awidth%3A%202%0Acolor%3A%20%23FFFFFF%0A%0Aactions%3A%0A%20%20-%20%3D%3E%20rotate%28-90%29%0A%20%20%2B%20%3D%3E%20rotate%2890%29%0A%20%20F%20%3D%3E%20draw%28%29 " sandbox> </iframe> </iframe> ---- <iframe width="100%" height="500" src="https://jobtalle.com/lindenmayer_systems.html" sandbox> </iframe> ---- https://video.twimg.com/tweet_video/E9ta1HPXIAET6ru.mp4 <iframe width="100%" height="500" src=" https://video.twimg.com/tweet_video/E9ta1HPXIAET6ru.mp4 " sandbox></iframe> ---- [https://hub.ovh2.mybinder.org/user/thomaslenne-terminale-nsi-cours-2ffrwida/notebooks/__Projets__/13.L-Systems/L_Systems.ipynb](https://hub.ovh2.mybinder.org/user/thomaslenne-terminale-nsi-cours-2ffrwida/notebooks/__Projets__/13.L-Systems/L_Systems.ipynb )  ---- <iframe width="100%" height="500" src="https://blog.univ-angers.fr/mathsinfo/2024/09/30/fractales/" > </iframe> ---- https://xymaths.fr/MathAppli/Fractales-IFS-Jeu-du-chaos/ https://www.fil.univ-lille.fr/~wegrzyno/Stage_IREM_2011/L-Systemes/index.html --- # hasard ---- https://xymaths.fr/MathAppli/Fractales-IFS-Jeu-du-chaos/Liste-Fractales.php#s7 ---- ---- ---- --- # IFS systèmes de fonctions itérées 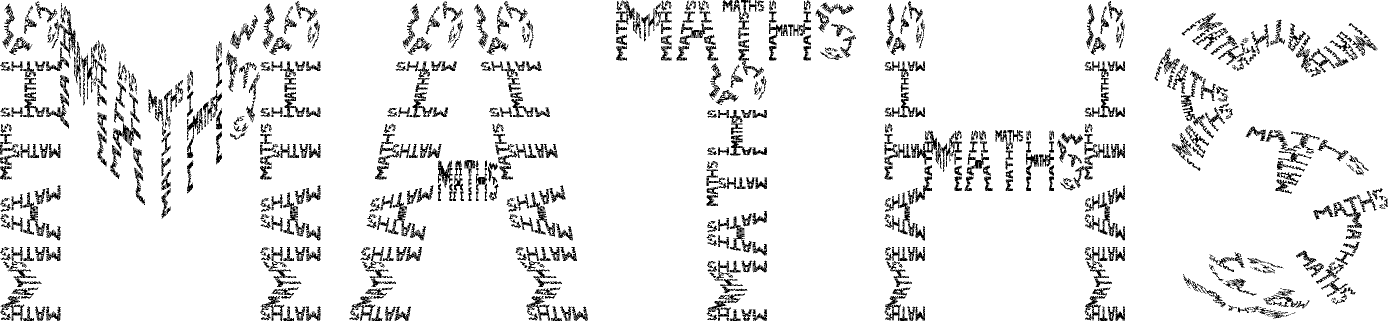La construction d’image s’effectue ici par copie d’elle-même. Mais à chaque copie, l’image copiée subit une transformation géométrique (une transformation linéaire représentée en mathématique par une fonction linéaire). Ces transformations peuvent être des rotations, des aplatissement, des cisaillements… Les copies sont également contractées avant d’être replacées sur l’image d’origine. Le processus est répété jusqu’à former une image ---- https://sorciersdesalem.math.cnrs.fr/IFS/ifs.html <iframe width="100%" height="500" src=" https://sorciersdesalem.math.cnrs.fr/IFS/ifs.html " sandbox> </iframe> ----  ----  ----  ---- https://math.univ-lille1.fr/~bodin/fichiers/ch_ifs.pdf  ---- https://larryriddle.agnesscott.org/ifs/ifs.htm <iframe width="100%" height="500" src=" https://larryriddle.agnesscott.org/ifs/siertri/ifsAnimation.htm " sandbox> </iframe> </iframe> ----  ---- {%youtube wAP-WkmewBU&t=226s %} ----  ---- https://mathematica.stackexchange.com/questions/159814/how-to-make-an-fractal-text-by-using-mathematica  ---- https://www.mathenjeans.fr/sites/default/files/comptes-rendus/ifs_presentation_louisemichel_94.pdf ---- https://docs.gimp.org/2.10/fr/plug-in-ifscompose.html ---- http://www.edboas.com/science/ftext/index.html  ---- https://ismaelsb.shinyapps.io/FractalText/  ----   ---- 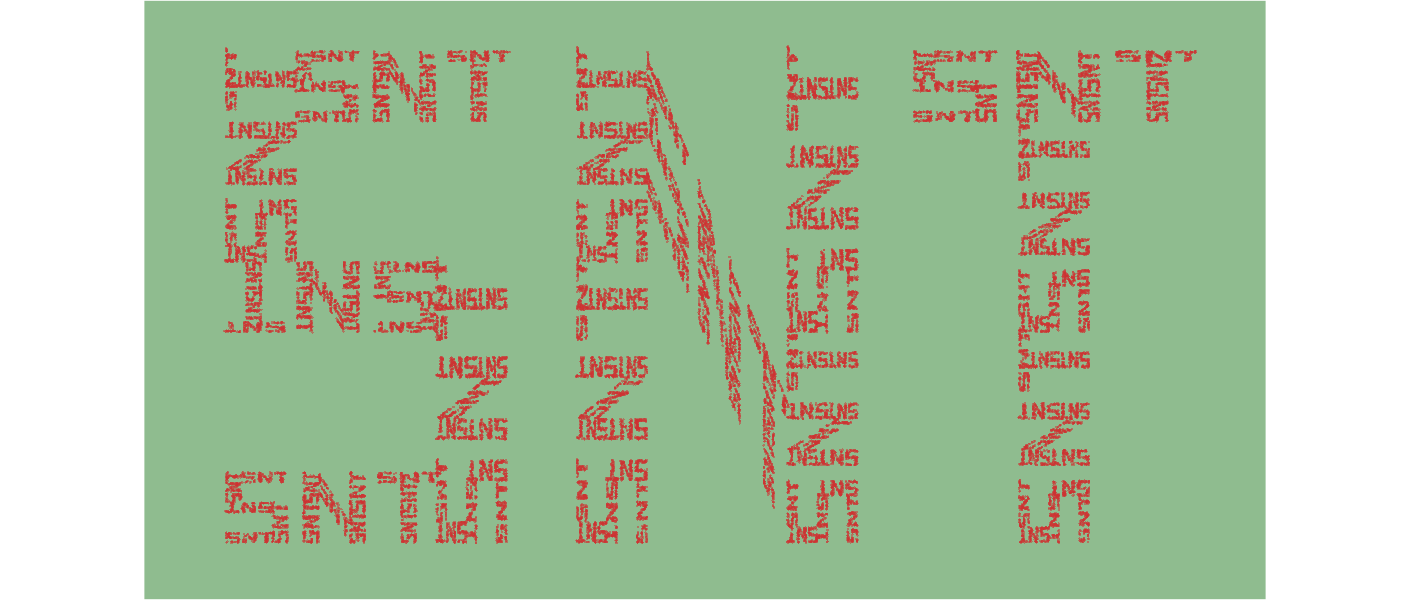https://mathematica.stackexchange.com/questions/159814/how-to-make-an-fractal-text-by-using-mathematica  --- # Lichtenberg: allumer le feu Les fractales de Lichtenberg sont réalisées par le biais d’un courant électrique envoyé dans le bois. L’électricité, en cherchant à se frayer un chemin va brûler le bois sur son passage et laisser ainsi ces fameuses fractales. ---- {%youtube DBCtZLPxbXA?%} t=4mn ---- <iframe width="100%" height="500" src=" https://montaga.github.io/droste/ " sandbox> </iframe> ---- ---- <iframe width="100%" height="500" src=" https://cindyjs.org/gallery/cindygl/HumanTree/index.html " sandbox> </iframe> ---- https://montaga.github.io/posenet/ https://montaga.github.io/tdot/ ---- Activité Elèves 2nd Séance 1 : découverte des fractales avec Xaos l’énoncé Séance 2 : construction de fractales avec Geoegbra l’énoncé Séance 3 : construction de fractales avec le module turtle de Python l’énoncé Séance 4 : construction de fractales avec le module PIL de Python l’énoncé https://frederic-junier.org/MPS2014/MPS-2017-Fractales-Seance1.pdf https://frederic-junier.org/MPS2014/MPS-2017-Fractales-Seance2.pdf https://frederic-junier.org/MPS2014/MPS-2017-Fractales-Seance3.pdf https://frederic-junier.org/MPS2014/MPS-2017-Fractales-Seance4.pdf