<style> mark{ background: yellow; font-weight: bold; } // https://lucidar.me/fr/web-dev/css-color-list/ </style> # DNB Juin 2025 Amérique du Nord : une correction du sujet de mathématiques > *Conçu à partir du [sujet original](http://college.valdugy.free.fr/IMG/pdf/dnb_juin2025_ameriquedunord_original.pdf) proposé par le [Café Pédagogique](https://cafepedagogique.net/2025/06/06/decouvrez-les-sujets-du-diplome-national-du-brevet-en-amerique-du-nord/) et de sa transcription TeX par l'[APMEP](https://www.apmep.fr/Brevet-2025)* > *Merci aux relecteurs/correcteurs du groupe ArCSiN de l'[IREM de Lille](https://irem.univ-lille.fr/) ainsi que Inés, Charly, Fanny, Lucas, Cassandra, Laly et Matthieu.* > (c) CC by-Nc - 9/10 juin 2025 - Keops ([E.Ostenne](mailto:emmanuel.ostenne@ac-lille.fr?subject=CodiDNBjuin2025)) # Exercice 1 (20 points) ## Situation 1 Dans une urne de $40$ boules indiscernables au toucher, $5$ sont rouges, $20$ sont vertes et $15$ sont blanches. L'expérience consiste à tirer au hasard une boule de l'urne et à noter sa couleur. Calculer la probabilité d'obtenir une boule verte. :::success ::: spoiler ++Correction++ 20 boules sont vertes sur les 40 contenues dans l’urne. La probabilité d’obtenir une boule verte est égale à $\dfrac{20}{40}$, soit $\dfrac{1}{2}$ ou 0,5 ou <mark>50 %</mark>. ::: ## Situation 2 Décomposer en produit de facteurs premiers le nombre $1050$. *Aucune justification n’est attendue.* :::success ::: spoiler ++Correction++ *La justification n'était pas demandée.* 1 050 = 2 × 525 = 2 × 3 × 175 = 2 × 3 × 5 × 35 = 2 × 3 × 5 × 5 × 7 La décomposition en produit de facteurs premiers de 1 050 est donc <mark>2 × 3 × 5^2^ × 7</mark>. ::: ## Situation 3 Un article coûte 25 €. Calculer son prix après une augmentation de 14 %. :::success ::: spoiler ++Correction++ Un article coûte 25 €. Calculer son prix après une augmentation de 14 %. Appelons a l’augmentation : | | Prix article (€) | Pourcentage (%) | | ------ |:----------------:|:---------------:| | Partie | a | 14 | | Total | 25 | 100 | donc a = $\dfrac{14×25}{100}$ = 3,5 L’article a augmenté de 3,50 €. 25+3,5 = 28,5 L’article coûte après augmentation <mark>28,50 €</mark>. ::: ## Situation 4 Le polygone 2 est un agrandissement du polygone 1. 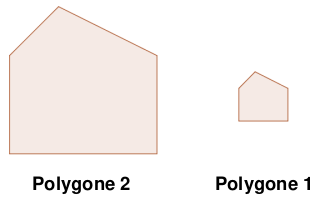*La figure ci-dessous n'est pas à l'échelle.*  Le coefficient de cet agrandissement est $2,5$. L'aire du polygone 1 est égale à $7,5$ cm^2^. Calculer l'aire du polygone 2. :::success ::: spoiler ++Correction++ Dans une homothétie (agrandissement) de rapport k les aires sont multipliées par k². donc Aire2=k²×Aire1 Comme ici k=2,5 on a donc Aire2=2,5²×7,5 Aire2=46,875 Donc l’aire du polygone 2 fait <mark>46,875 cm²</mark>. ::: ## Situation 5 Dans une classe de 3^e^ on note la répartition des tailles des élèves dans le tableau suivant: | Taille (en cm) | 152 | 157 | 160 | 162 | 165 | 170 | 174 | 180 | |:--------------:|:---:|:---:|:---:|:---:|:---:|:---:|:---:|:---:| | Effectif | 2 | 4 | 2 | 5 | 2 | 4 | 6 | 5 | a. Quelle est la moyenne des tailles des élèves de cette classe ? :::success ::: spoiler ++Correction++ a) L'effectif total est de 30 élèves car 2+4+...+5 = 30. Comme 152×2+157×4+...+180×5 = 5016, la moyenne s'obtient par : $\dfrac{5016}{30}$ = 167,2 La taille moyenne fait <mark>167,2 cm</mark>. ::: b. Quelle est la médiane des tailles des élèves de cette classe ? :::success ::: spoiler ++Correction++ D’après la question précédente, il y a 30 élèves dans la classe et 30÷2=15, donc la médiane est entre la 15^e^ et la 16^e^ taille quand elles sont rangées dans l’ordre croissant. 2+4+2+5+2=15 : les tailles de 152 à 165 cm sont les 15 plus petites. Donc la médiane fait <mark>167,5 cm</mark>. 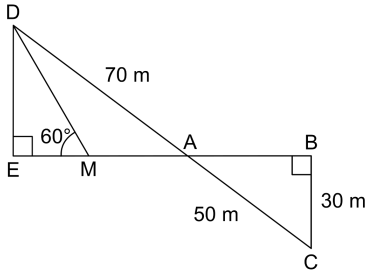<u>Remarques</u> : -*Une valeur médiane m telle que 165<m<170 conviendrait aussi.* -*Alternative : on pourrait construire un tableau des effectifs cumulés croissants.* ::: # Exercice 2 (20 points) *La figure ci-dessous n’est pas en vraie grandeur.*  On a les données suivantes : * Les points A, B, E et M sont alignés. * Les points A, C et D sont alignés. * ADE est un triangle rectangle en E. * ABC est un triangle rectangle en B. * AD $= 70$ m. * BC $= 30$ m. * AC $= 50$ m. * $\widehat{\text{DME}} = 60°$. 1. Calculer la longueur AB. :::success ::: spoiler ++Correction++ Dans le triangle ABC rectangle en B, d'après la propriété de Pythagore, AC²=AB²+BC² 50²=AB²+30² 2500=AB²+900 AB²=2500-900 AB²=1600 AB=$\sqrt{1600}$ AB=40 donc <mark>AB=40 m</mark> ::: 2. Montrer que les droites (DE) et (BC) sont parallèles. :::success ::: spoiler ++Correction++ Les droites (DE) et (BC) sont perpendiculaires à la même droite (AB) donc <mark>(DE)//(BC)</mark>. ::: 3. Montrer que la longueur DE est égale à $42$ m. :::success ::: spoiler ++Correction++ Ainsi on reconnaît une configuration de Thalès "sablier" avec : - les droite (DC) et (EB) sécante en A - (DE)//(BC) donc, d'après la propriété de Thalès, $\dfrac{AE}{AB}=\dfrac{AD}{AC}=\dfrac{DE}{BC}$ $\dfrac{AE}{40}=\dfrac{70}{50}=\dfrac{DE}{30}$ d'où $DE=\dfrac{70×30}{50}$ donc <mark>DE=42 m</mark>. ::: 4. Montrer que la longueur EM est environ égale à $24,2$ m. :::success ::: spoiler ++Correction++ Dans le triangle DEM rectangle en E, tan($\widehat{DME}$)=$\dfrac{DE}{EM}$ tan(60°)=$\dfrac{42}{EM}$ d'où $EM=\dfrac{42}{tan(60°)}$ donc $EM \approx 24,249$ Ainsi <mark>EM est environ égale à 24,2 m</mark>. ::: 5. En déduire l'aire du triangle AMD. :::success ::: spoiler ++Correction++ Aire(AMD)=Aire(ADE)-Aire(DME) -Aire(ADE)=$\dfrac{AE × DE}{2}$ D'après la question 3., $\dfrac{AE}{40}=\dfrac{70}{50}$ d'où $AE=\dfrac{70 × 40}{50}$ donc AE= 56 m. D'où Aire(ADE)=$\dfrac{AE × DE}{2}$ donc Aire(ADE)=$\dfrac{56 × 42}{2}$ ainsi **Aire(ADE)= 1176 m².** -Aire(DME)=$\dfrac{EM × DE}{2}$ D'après la question 4., $EM \approx 24,2$. D'où Aire(DME)=$\dfrac{EM × DE}{2}$ donc Aire(DME)≈$\dfrac{24,2 × 42}{2}$ ainsi **Aire(DME)≈508,2 m².** Comme Aire(AMD)=Aire(ADE)-Aire(DME), Aire(AMD)≈1176-508,2. Donc <mark>Aire(AMD)≈667,8 m²</mark>. ::: # Exercice 3 (20 points) | Programme A | | ----------- | | • Choisir un nombre <br> • Multiplier par 3 <br> • Ajouter 15 <br> • Diviser par 3 <br> • Soustraire le nombre de départ | | Programme B | | ----------- | ```graphviz digraph hierarchy { node [shape=box] A [label=" Choisir un nombre "] B [label=" Soustraire 1 "] C [label=" Soustraire 6 "] D [label=" Multiplier les deux résultats obtenus "] E [label=" Ajouter 5 "] A->B A->C B->D C->D D->E } ``` 1. Montrer que, lorsque le nombre choisi est 4, le résultat obtenu avec le programme A est 5. :::success ::: spoiler ++Correction++ • Choisir un nombre : 4 • Multiplier par 3 :4×3=12 • Ajouter 15 : 12+15=27 • Diviser par 3 : 27÷3=9 • Soustraire le nombre de départ : 9-4=<mark>5</mark> ::: 2. Montrer que, lorsque le nombre choisi est $- 2$, le résultat obtenu avec le programme A est 5. :::success ::: spoiler ++Correction++ • -2 • -2×3=-6 • -6+15=9 • 9÷3=3 • 3-(-2)=3+2=<mark>5</mark> ::: 3. Justifier que l'affirmation suivante est vraie : " Le programme A donne toujours le même résultat. " :::success ::: spoiler ++Correction++ Appelons x le nombre à choisir et faisons le programme A : • x • x×3=3x • 3x+15 • (3x+15)÷3=x+5 • x+5-x= **5** Donc il est <mark>vrai</mark> que le programme donne toujours le même résultat qui est 5. ::: 4. Lorsque le nombre choisi est 10, quel résultat obtient-on avec le programme B ? :::success ::: spoiler ++Correction++ ```graphviz digraph hierarchy { node [shape=box] A [label=" Choisir un nombre : 10 "] B [label=" Soustraire 1 : 10-1=9 "] C [label=" Soustraire 6 : 10-6=4 "] D [label=" Multiplier les deux résultats obtenus : 9×4=36 "] E [label=" Ajouter 5 : 36+5= 41 "] A->B A->C B->D C->D D->E } ``` Avec 10 choisi, le résultat du programme B est <mark>41</mark>. ::: 5. Il existe exactement deux nombres pour lesquels les programmes A et B fournissent à chaque fois des résultats identiques. Quels sont ces deux nombres? :::success ::: spoiler ++Correction++ Appelons x le nombre à choisir et faisons le programme A : ```graphviz digraph hierarchy { node [shape=box] A [label="Choisir un nombre : x "] B [shape=box, label="Soustraire 1 : x-1"] C [shape=box, label="Soustraire 6 : x-6"] D [shape=box, label="Multiplier les deux résultats obtenus : (x-1)×(x-6)"] E [shape=box, label="Ajouter 5 : (x-1)×(x-6)+5"] A->B A->C B->D C->D D->E } ``` L'expression du programme B est (x-1)×(x-6)+5, l'expression du programme A est 5. Donc il faut résoudre l'équation (x-1)×(x-6)+5=5. Ce qui revient à résoudre (x-1)×(x-6)=0. Si a×b=0 alors a=0 ou b=0. Ainsi (x-1)=0 ou (x-6)=0 soit x=1 ou x=6. Les deux nombres cherchés sont <mark>1 et 6</mark>. ::: # Exercice 4 (20 points) À l'approche d'une course organisée par son collège, Malo s'entraîne sur un parcours de $13,5$ km. La courbe ci-dessous représente la distance parcourue par Malo (en kilomètres) en fonction du temps écoulé (en minutes).  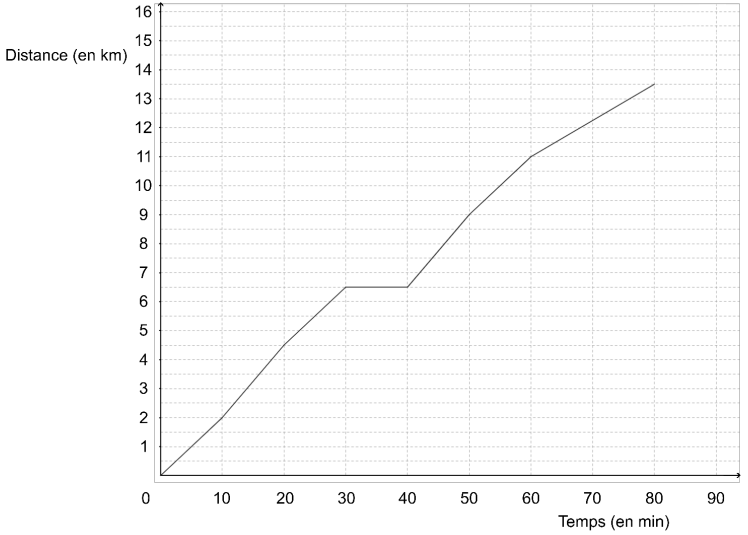1. Le temps et la distance parcourue par Malo sont-ils proportionnels ? :::success ::: spoiler ++Correction++ La courbe sur le graphique distance en fonction du temps n'est pas une droite donc <mark>le temps et la distance ne sont pas proportionnels</mark>. ::: 2. Quelle distance Malo a-t-il parcourue au bout de 20 minutes ? *Aucune justification n'est attendue.* :::success ::: spoiler ++Correction++ *La justification n'était pas demandée.* Sur le graphique, le point d'abscisse 20 a pour ordonnées 4,5 donc Malo a parcouru <mark>4,5 km</mark> au bout de 20 min. ::: 3. Combien de temps a-t-il mis pour faire les 9 premiers kilomètres ? *Aucune justification n'est attendue.* :::success ::: spoiler ++Correction++ Sur le graphique, le point d'ordonnée 9 a pour abscisse 50 donc Malo a parcouru 9 km au bout de <mark>50 min</mark>. ::: 4. Quelle est la vitesse moyenne de Malo lors de cette course? Exprimer le résultat au dixième de km/h près. :::success ::: spoiler ++Correction++ v=$\dfrac{d}{t}$ Sur le graphique le point d'ordonnée 13,5 a pour abscisse 80 donc Malo a fait le parcours de 13,5 km en 80 min. | distance (km) | 13,5 | d | |:-------------:|:----:|:---:| | temps (min) | 80 | 60 | donc d=$\dfrac{13,5 × 60}{80}$ soit d=10,125 Ainsi, avec sa vistesse moyenne, Malo a parcouru 10,125 km en 1 heure, il est allé à la vitesse moyenne de <mark>10,1 km/h environ</mark>. ::: 5. Louise et Hillal ont couru sur le même parcours de $13,5$ km. Louise a une vitesse régulière égale à $12$ km/h et Hillal a une vitesse régulière égale à $10$ km/h. **a**. Sachant que Louise et Hillal sont partis en même temps, qui a été le premier à franchir la ligne d'arrivée ? :::success ::: spoiler ++Correction++ Comme Louise a une vitesse plus grande que Hillal, c'est <mark>Louise</mark> qui a passé la ligne d'arrivée en premier. ::: **b**. Quelle distance sépare Louise et Hillal, lorsque le premier des deux franchit la ligne ? :::success ::: spoiler ++Correction++ Louise a parcouru les 13,5 km à la vitesse de 12 km/h donc elle a mis un temps t pour arriver tel que : | distance (km) | 13,5 | 12 | |:-------------:|:----:|:---:| | temps (h) | t | 1 | Ainsi t=$\dfrac{13,5×1}{12}$=1,125 Elle a mis 1,125 h pour faire le parcours. Hillal pendant ce même temps a parcouru une distance d. Comme il va à 10 km/h, on a : | distance (km) | d | 10 | |:-------------:|:-----:|:---:| | temps (h) | 1,125 | 1 | d'où d=$\dfrac{10×1,125}{1}=11,25 Ainsi Hillal a parcouru 11,25 km quand Louise est arrivée. 13,5-11,25=2,25 donc il y a <mark>2,25 km</mark> d'écart quand Louise est arrivée. ::: # Exercice 5 (20 points) *Dans cet exercice, aucune justification n’est attendue.* ## Partie 1 : les motifs | Script 1 | Script 2 | Script 3 | |:------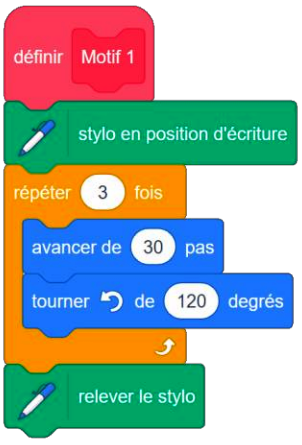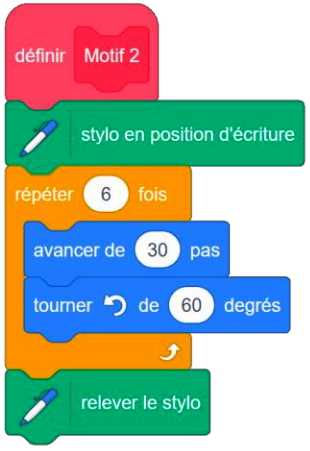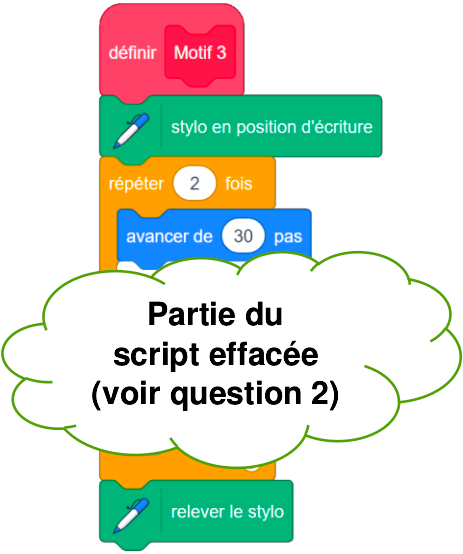------------------------------------------------------------------------------------------: | :------: | :------: | |  |  |  | 1. Les scripts 1 et 2 permettent chacun d’obtenir un des dessins ci-dessous. Associer chacun des scripts à son dessin. | Desssin 1 | Dessin 2 | |:---------:|:--------:| | 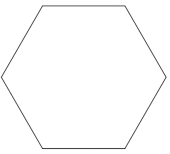 | 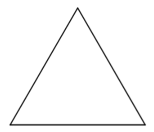 | :::success ::: spoiler ++Correction++ *La justification n'était pas demandée.* Le nombre de répétitions pour la boucle [répéter] indique le nombre de côtés tracés grâce aux blocs <span style=" background:royalblue; color:white;">[avancer]</span> puis <span style=" background:royalblue; color:white;">[tourner]</span> : * le triangle a 3 côtés donc <mark>le Script 1 est associé au Dessin 2</mark>, * l'hexagone a 6 côtés donc <mark>le Script 2 est associé au Dessin 1</mark>. ::: 2. 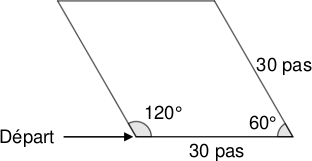Le script 3 permet d'obtenir le losange ci-dessous :  La partie du script effacée contient les 3 instructions A, B et C ci-dessous. Sur votre copie, recopier dans le bon ordre les instructions cachées. **Chaque instruction ne doit être utilisée qu'une seule fois.** | Instruction A | Instruction B | Instruction C | 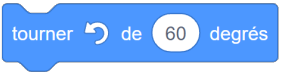|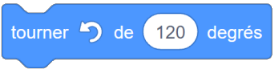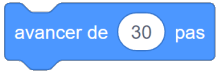:--------------------------------------------------------------------------------------:|:--------------------------------------------------------------------------------------:|:--------------------------------------------------------------------------------------:| |  |  |  | :::success ::: spoiler ++Correction++ *La justification n'était pas demandée.* L'ordre des instructions sera <mark>B-C-A</mark>. En effet, avant la partie éffacée, le bloc <span style=" background:royalblue; color:white;">[avancer]</span> fait avancer le lutin (vers la droite) de 30 pas pour dessiner le premier côté en bas : le lutin arrive en bas à droite du segment. Comme le lutin "regarde" alors vers l'extérieur (vers la droite), il ne va pas tourner de 60° mais de 120° (180°-60°=120°) pour se positionner avant de dessiner le côté second côté. D'où **l'instruction B est en premier**. Ensuite il avance pour tracer ce second côté codé 30 pas à droite. D'où **l'instruction C en en deuxième**. Reste **l'instuction A en dernier**, pour repositionner le lutin afin de tracer le 3e côté du haut. 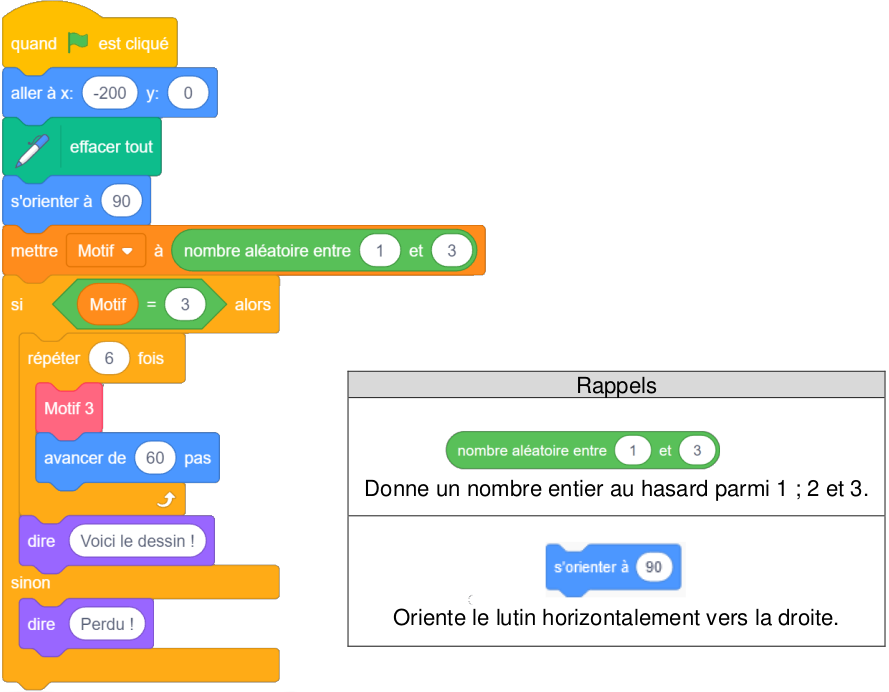::: ## Partie 2 : le script principal  3. Quelles sont les coordonnées du point de départ du lutin ? :::success ::: spoiler ++Correction++ *La justification n'était pas demandée.* Le lutin est aux coordonnées <mark>(-200;0)</mark> quand il va commencer à dessiner car, une fois le drapeau vert cliqué et donc le programme démarré, le premier bloc est ln bloc déplacement du lutin [aller à x:-200 y:0]. ::: 4. Parmi les 5 captures d’écran proposées ci-dessous, seules deux sont possibles. Lesquelles ? | Titre | Image | |:---------------------:|:-----:| | Capture d’écran n° 1 | 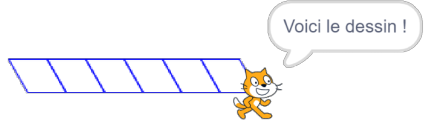 | | Capture d’écran n° 2 | 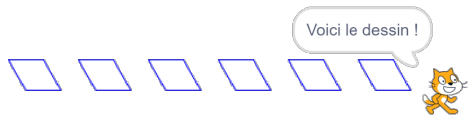 | | Capture d’écran n° 3 |  | | Capture d’écran n° 4 | 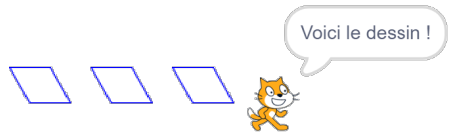 | | Capture d’écran n° 5 |  | :::success ::: spoiler ++Correction++ *La justification n'était pas demandée.* <mark>Les captures d'écrans 2 et 3</mark> sont les seules pouvant convenir. Dans le bloc conditionnel <span style=" background:darkorange;color:white;">[si]</span> on voit 2 alternatives, <span style=" background:darkorange;color:white;">[alors]</span> et <span style=" background:darkorange;color:white;">[sinon]</span> : - <span style=" background:darkorange;color:white;">[alors]</span> : c'est d'abord le bloc <span style=" background:deeppink; color:white;">[Motif 3]</span> pour dessiner le losange, puis <span style=" background:royalblue; color:white;">[avancer]</span> pour déplacer le lutin de 60 pas : une fois le motif dessiné, le lutin est revenu à son point de départ et dans sa posture de départ. Il ne dessine alors plus : voir bloc <span style=" background:green;color:white;">[relever]</span>. Quand il avance de 30 pas, il arrive au point en bas à droite du motif, puis il doit encore avancer de 30 pas à droite hors du motif toujours sans laisser de trace. Donc il y aura un "trou" entre le losange dessiné et le suivant : seuls les captures n°2 et n° 4 pourraient convenir. Comme il y a 6 répétitions dans la boucle <span style=" background:darkorange;color:white;">[répéter]</span>, il y a 6 motifs dessinés. Donc seule **la capture n°2** convient. - <span style=" background:darkorange;color:white;">[sinon]</span> : il n'y a qu'un bloc <span style=" background:darkorchid;color:white;">[dire]</span> pour afficher "Perdu !", donc seule la **capture n°3** convient. ::: 5. On clique sur le drapeau vert, et on observe le message affiché. Quelle est la probabilité que le message affiché soit « Voici le dessin! » ? :::success ::: spoiler ++Correction++ *La justification n'était pas demandée.* Il est dit que le bloc <span style=" background:green;color:white;">[nombre aléatoire]</span> donne un nombre entier parmi 1,2 et 3 tiré au hasard. Quand ce nombre est 3, le programme dessine le motif 3 puis affiche "Voici le dessin!". Donc il y a 1 chance sur 3 que "Voici le dessin!" soit affiché. La probabilité est de $\dfrac{1}{3}$ ou environ 0,33 ou <mark>environ 33%</mark>. ::: 6. On lance de nouveau le programme 100 fois et on regroupe les résultats obtenus dans le tableau suivant: | Message du lutin | "Voici le dessin !" | "Perdu !" | |:-----------------:|:-------------------:|:---------:| | Effectif | 40 | 60 | **a**. Calculer la fréquence de l’affichage "Voici le dessin !". :::success ::: spoiler ++Correction++ La fréquence d'une valeur s'obtient en divisant l'effectif de la valeur par l'effectif total. On a obtenu 40 fois la valeur "Voici le dessin!" parmi les 100 valeurs. La fréquence est donc $\dfrac{40}{100}$ ou 0,4 ou <mark>40%</mark>. ::: **b**. Pourquoi ce résultat est-il différent de celui obtenu à la question 5 ? :::success ::: spoiler ++Correction++ La probabilité obtenue à la question 5 est une valeur théorique vers laquelle tendrait la valeur expérimentale qu'est la fréquence obtenue à la question 6.a. Il faudrait jouer énormément de fois pour que la valeur expériementale se stabilise autour de cette valeur théorique à quelques décimales près. On a joué "très peu" - 100 fois - donc avoir <mark>des résultats différents</mark> n'a rien d'anormal. <u>Alternative :</u> 100 n'étant pas dans la table de 3, il est impossible d'obtenir une fréquence d'exactement $\dfrac{1}{3}$ comme à la question 5. Au plus proche, comme les effectifs sont entiers, la fréquence pouvait être de $\dfrac{33}{100}$ si l'effectif était 33 et $\dfrac{34}{100}$ si l'effectif était 34 : $\dfrac{33}{100} < \dfrac{1}{3} < \dfrac{34}{100}$. Donc **les résultats des questions 5 et 6 sont nécessairement différents.** :::