# 2024 # centenaire # MANDELBROT ## ensembles de julia et mandelbrot --- # Deux outils simplissimes $$i^2=-1$$ $$&$$ $$f(x)=x^2$$ ---- ## fonction itérée On part d'une valeur $x_0$ et on applique plusieurs fois de suite la fonction $f$ - Cette suite tendra rapidement vers l’infini pour toutes les valeurs $x_0$ plus grandes que 1. $2,4,16,256,...$ - Elle restera sur 1 pour $x_0$ égal à 1, et elle tendra vers 0 pour les valeurs $x_0$ entre -1 et 1. 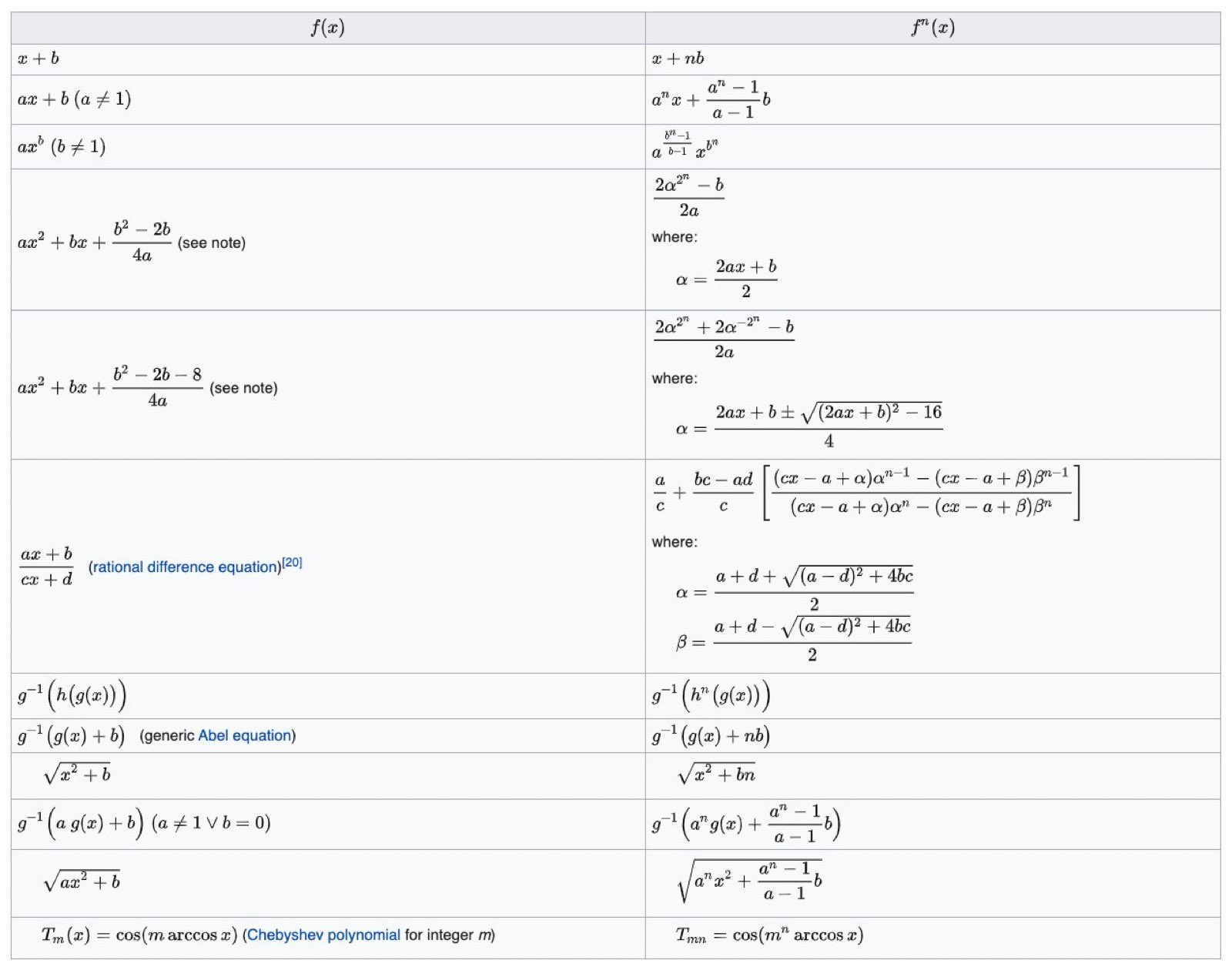$0,5;0,25;...$ ---- ia et fonctions itérées  --- en 1D  en 2D  --- # ensemble de Julia $J_c$ $f(z)=z^2+c$ , avec $c$ un complexe exemple pour c=-0,75: la basilique (ou dragon de San Marco  ---- c=i : la dendrite de Julia, qu’on retrouve entre autres sur les parties extérieures de l’ensemble, à la hauteur de ce qui semble être des droites…  ---- C=-0,123+0.745i : le lapin de Douady  ---- <iframe width="1000" height="800" src="https://experiences.mathemarium.fr/Julia-sets.html" > </iframe> ---- [](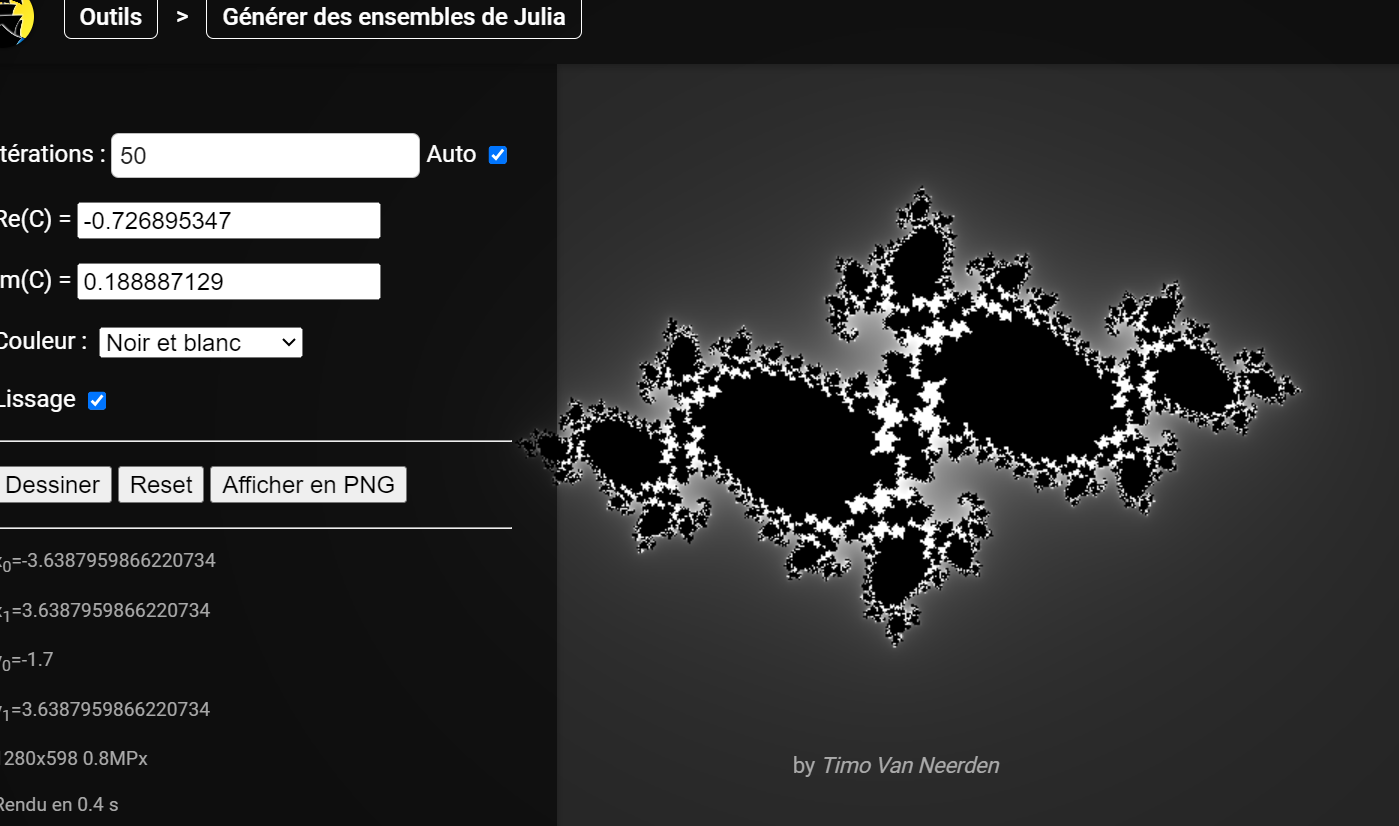https://lehollandaisvolant.net/tout/tools/mandelbrot/julia.php#zoom=7.277591973244147,3.4&lookAt=0,0&iterations=85&colorScheme=pickColorGrayscale ) ---- <iframe width="100%" height="500" src=" https://mathcurve.com/fractals/julia/julia.shtml " sandbox></iframe> ---- [travail expert](https://www.lelivrescolaire.fr/page/12582188) https://maths-au-quotidien.fr/lycee/docs/Ensembles-de-Julia.pdf --- <p style="font-family: ARCHIVE ; font-size:19pt">JULIA VS MANDELBROT </p> Soit la suite $z$ telle que : $z_{n+1}=z_{n}^{2}+c$ , commençant à $z_0$ avec $c\in\mathbb{C}$ Pour l'ensemble de Julia: on fixe une valeur $c$ et on regarde pour quelles valeurs $z_0$ , la suite n'explose pas Pour l'ensemble de Mandelbrot: on fixe $z_0$ à 0 et on regarde pour quelles valeurs c , la suite n'explose pas --- # ensemble de Mandelbot  ---- {%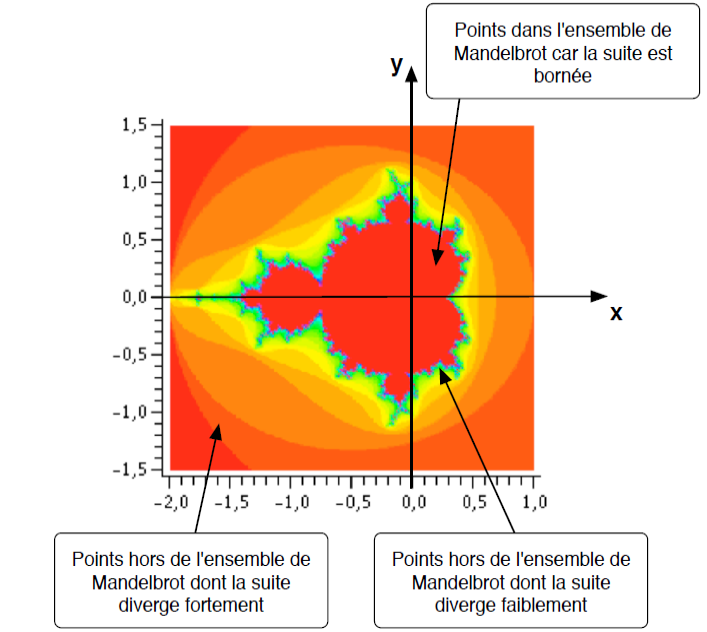youtube aSg2Db3jF_4 %} ----   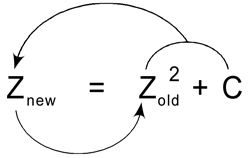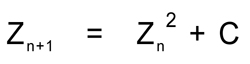avec $$\huge{z_0=0}$$ ---- pour c=1, on obtient:  ---- 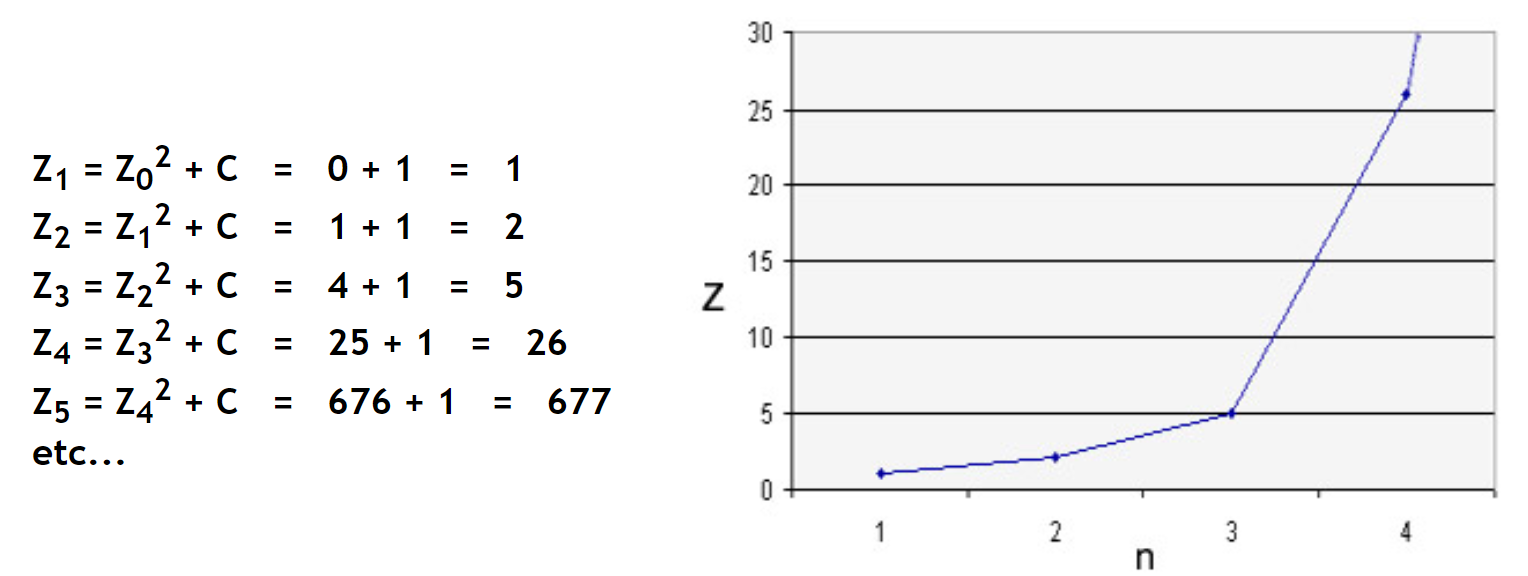pour c=-0.5, on obtient:  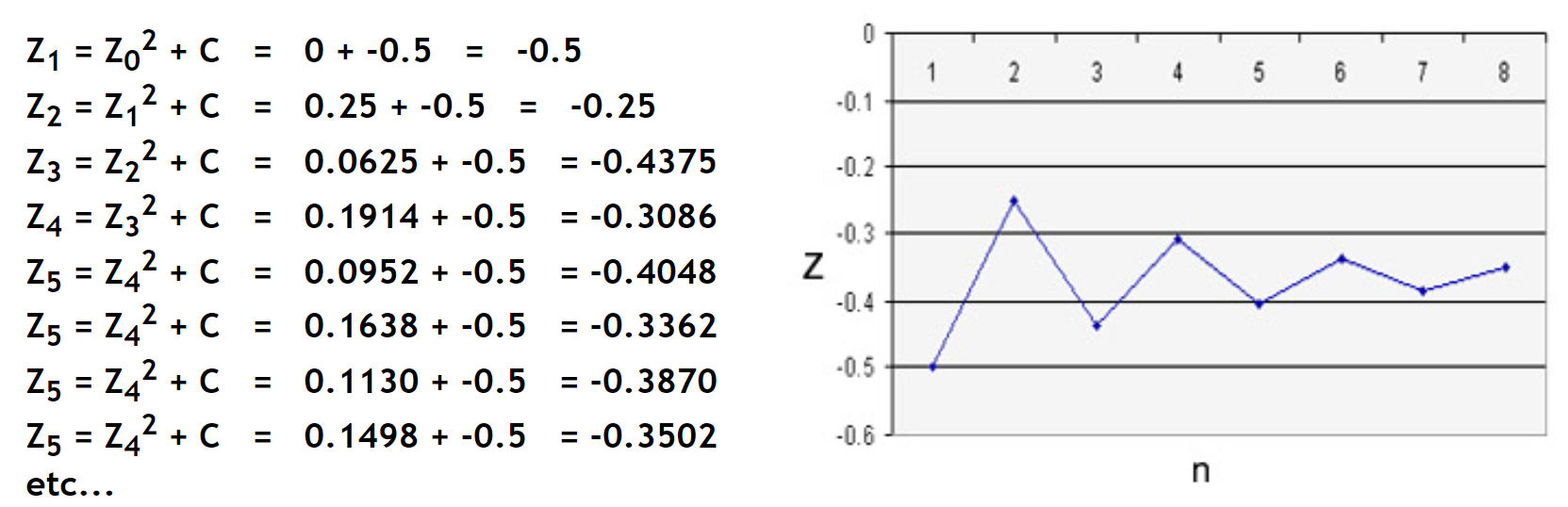https://fractalfoundation.org/OFC/OFC-index.htm ---- <iframe width="100%" height="500" src=" https://www.geogebra.org/material/iframe/id/hvuaudu6/width/800/height/594/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/true/rc/false/ld/false/sdz/true/ctl/true " sandbox></iframe> ---- https://www.geogebra.org/m/NjENU4qC <iframe width="100%" height="500" src=" https://www.geogebra.org/m/nrbEKS9C" sandbox></iframe> ----  ---- https://euler.ac-versailles.fr/IMG/pdf/des_suites_complexes_aux_ensembles_fractals.pdf ---- https://complex-analysis.com/content/mandelbrot_set.html <iframe width="100%" height="500" src=" https://complex-analysis.com/applets/p5js/mandelbrot/ " sandbox></iframe> ----  ---- <iframe width="100%" height="500" src=" https://www.dynamicmath.xyz/complex/mandelbrotjulia/ " sandbox></iframe> ---- ## Liens entre l'ensrmble de Mandelbrot et l'ensemble de Julia  ---- 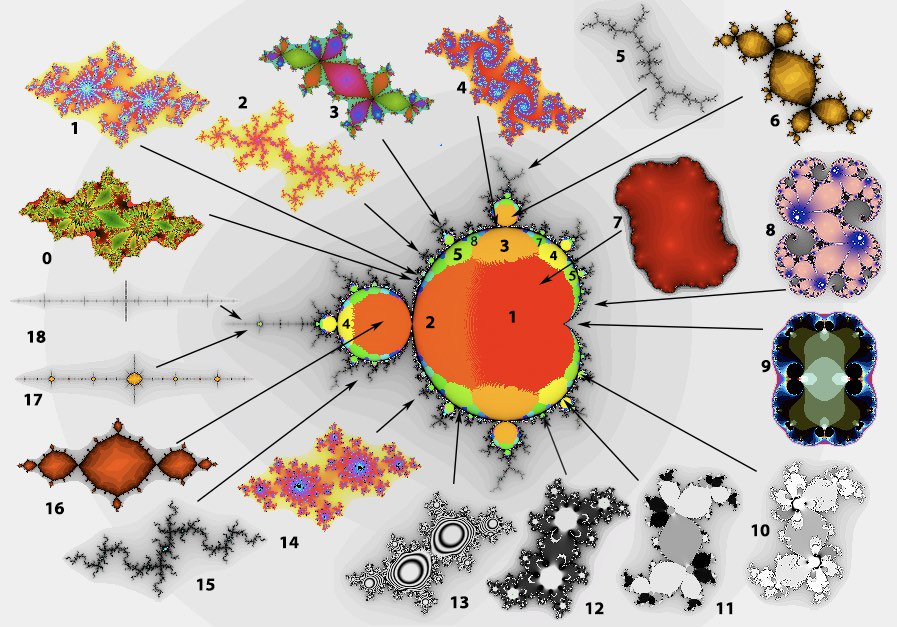https://www.dynamicmath.xyz/complex/mandelbrotjulia/ <iframe width="100%" height="500" src="https://www.dynamicmath.xyz/complex/mandelbrotjulia/ " > </iframe> ---- https://twitter.com/jcponcemath/status/1153282413834858497 --- https://fr.mathigon.org/course/fractals/mandelbrot --- # Vidéos --- Aller à t=6'27'' {%youtube JP0f9WQaOdk %} ---- {%youtube Y4ICbYtBGzA %} ---- {%youtube ovJcsL7vyrk %} ---- https://enseignants.lumni.fr/export/player/00000000662