# Correction - Évaluation non notée - Vitesse et proportionnalité ## Exercice 1 - Calculer une vitesse 1\. Pour convertir une distance en $\textrm{km}$ en $\textrm{m}$, on peut réaliser le tableau de conversion$~$: | | $\textrm{km}$ | $\textrm{hm}$ | $\textrm{dam}$ | $\textrm{m}$ | |:---: | :-: | :-: | :--: | :--: | | $1$ | $9$ | $6$ | $0$ | $0$ | Et on a donc, $19{,}6~\textrm{km}=19~600~\textrm{m}$ 2\. Pour convertir des durées, on se souvient que : $1~\textrm{min}=60~\textrm{s}$ On a alors : $21~\textrm{min}~18~\textrm{s}=21\times60~\textrm{s}+18~\textrm{s}=1278~\textrm{s}$ Ainsi, le coureur cycliste a mis $1278$ secondes pour parcourir $19~600$ mètres. 3\. Une vitesse moyenne est égale au rapport entre la distance parcourue et le temps écoulé. On a alors : $\displaystyle{}v=\frac{d}{t}$ $~~~~$ où $v$ est la vitesse, $d$ est la distance et $t$ est le temps. On procède au calcul : $\displaystyle{}v=\frac{19600~\textrm{m}}{1278~\textrm{s}}\approx{}15{,}33~\textrm{m/s}$ 4\. Pour convertir une vitesse en $\textrm{m/s}$ en $\textrm{km/h}$, on se souvient que : $1~\textrm{m/s}=3{,}6~\textrm{km/h}$ On a alors  : $15{,}33~\textrm{m/s}=15{,}33\times3{,}6~\textrm{km/h}=55{,}21~\textrm{km/h}$ La vitesse moyenne du coureur cycliste lors de ce contre-la-montre était donc d'envrion $55{,}21~\textrm{km/h}$. ## Exercice 2 - À partir de la hauteur de la tour Eiffel Sur le dessin de la Tour Eiffel, on mesure une hauteur de $4{,}7~\textrm{cm}$. \ On mesure une hauteur pour le deuxième étage de $1{,}7~\textrm{cm}$ \ On sait que la Tour Eiffel a une hauteur de $330~\textrm{m}$ (taille réelle). \ $~$ \ Puisqu'il y a proportionnalité entre la taille sur le dessin et la taille réelle. On a : | Taille dessin $\textrm{(cm)}$ | $4{,}7$ | $1{,}7$ | | :-: | :-: | :--: | | Taille réelle ($\textrm{m}$) | $330$ | $x$ | On en déduit alors : $\displaystyle{}x=\frac{1{,}7\times330}{4{,}7}\approx119$ \ Ainsi, la hauteur du deuxième étage est d'environ $119~\textrm{m}$ ## Exercice 3 - Augmentation du débit > **Analyse de l'énoncé :** \ > $143~\textrm{m}^3$ par seconde c'est le débit après l'augmentation de $30~\%{}$ à cause de la pluie. En proportion, le débit avant était de $100~\%{}$, avec les pluies il est passé à $130~\%{}$ (car $30\%{}$ de plus). a. Le débit est de $143~\textrm{m}^3$ par seconde après une augmentation de $30~\%{}$. \ On a alors l'égalité suivante : \ $\displaystyle{}\frac{143}{130}=\frac{d}{100}~~~~$ On en déduit alors que : $d=\displaystyle{}\frac{143\times100}{130}=110$ \ \ Ainsi, le débit avant augmentation était de $110~\textrm{m}^3$ par seconde. > Maintenant, le débit baisse de $30~\%$. C'est bien $30~\%{}$ du "nouveau" débit : $143~\textrm{m}^3$ par seconde. b. On calcule $30~\%$ de $143~\textrm{m}^3~$: $143\times{}30~\%{}=143\displaystyle{}\times\frac{30}{100}=42{,}9$. \ Le débit diminue donc de $42{,}9~\textrm{m}^3$, on calcule alors$~$: $143-42{,}9=100{,}1$ Finalement, le débit est donc de $100{,}1~\textrm{m}^3$ par seconde. ## Exercice 4 - Évolution des âges a. On a le tableau suivant : | Âge de la fille | $1$ | $3$ | $7$ | $15$ | $13$ | | :-: | :-: | :--: | :--: | :--: | :--: | | Âge du père | $24$ | $26$ | $30$ | $38$ | $36$ | b\. Plusieurs justifications possibles : - Lorsque la fille avait $0~\textrm{an}$, le père avait $23~\textrm{ans}$. Il n'y a donc pas proportionnalité entre l'âge du père et celui de sa fille. - Si on regarde la première colonne, on remarque que le coefficiant de proportionnalité _serait_ $24$ (puisque : $1\times24=24$). Or, ce coefficient ne s'applique pas à la deuxième colonne. En effet : $3\times24\ne26$. Il n'y a donc pas de coefficient de proportionnalité et donc l'âge du père et celui de sa fille ne sont pas proportionnels. - Enfin, on remarque que $1\times26\ne3\times24$, l'égalité du produit en croix n'est pas respectée, alors l'âge du père et celui de sa fille ne sont pas proportionnels. > **Remarque** \ > Une seule de ces justifications suffisait. Le fait que les "$13~\textrm{ans}$" de la fille apparaissent après ses "$15$ ans" n'est pas un argument en faveur ou en défaveur d'une proportionnalité entre les âges. \ Deux grandeurs peuvent être proportionelles sans que leurs données soient présentées de façon chronologique (ou rangées par ordre croissant) ## Exercice 5 - Monnaies et conversion a. On complète le tableau. > **Remarque** > Le plus simple étant de réaliser un retour à l'unité : $\displaystyle{}\frac{247{,}5}{5}=49{,}5$. Mais effectuer des calculs par "produit en croix" était aussi possible. :wink: | Euro (€) | $1$ | $5$ | $8$ | | :-: | :-: | :--: | :--: | | Roupie Mauricienne (Rs) | $49{,}5$ | $247{,}5$ | $396$ | b. 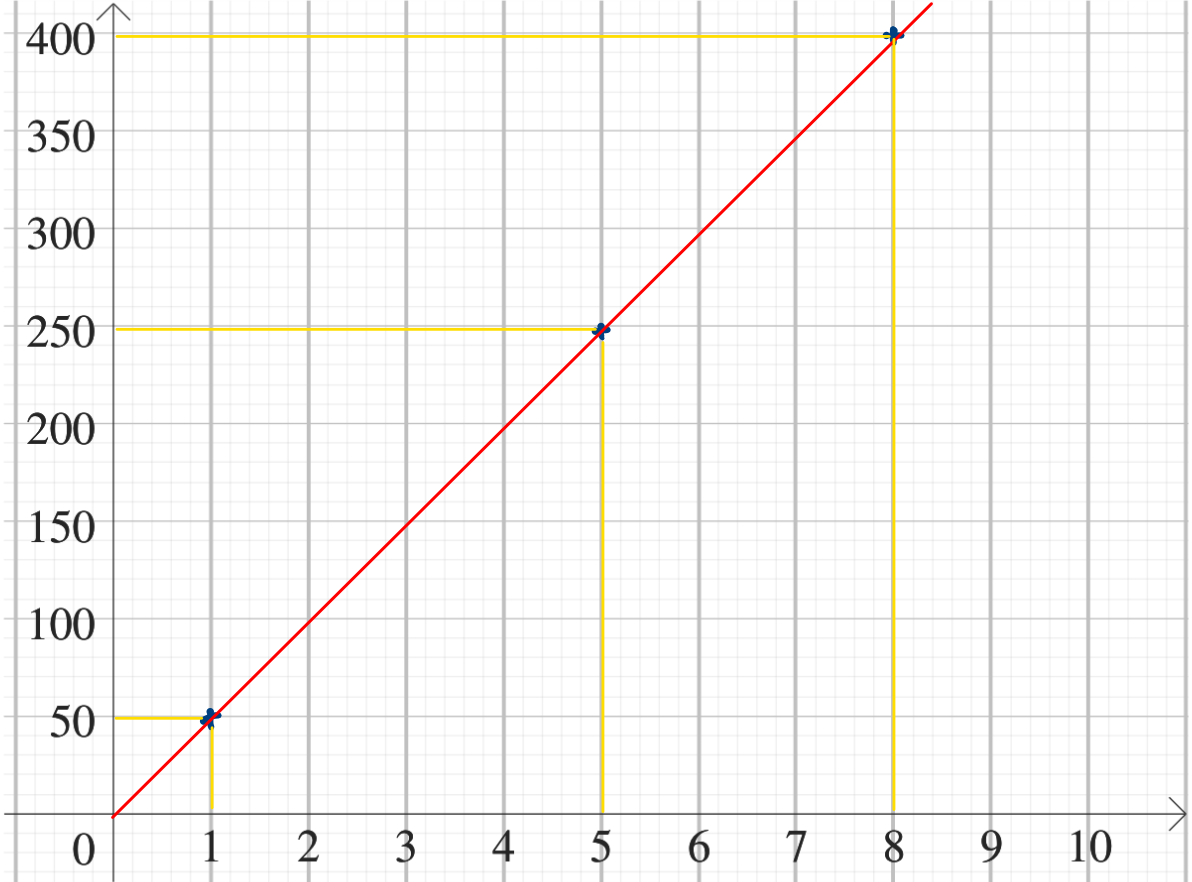 c. Les points sont tous alignés le long d'une **droite** qui **passe par l'origine** du repère. La situation représentée graphiquement est donc bien une situation de proportionnalité.