--- tags : Seconde, Géogebra langs : fr-fr title : Consignes « À la façon des maçons » --- <center>  </center> # Consignes « À la façon des maçons » ## Préalable - Vous allez construire une figure géométrique dynamique en utilisant *Géogébra* dans l'environnement *Capytale* puis effectuer un petit calcul. - **Enregistrer** votre travail avec le bouton  me permet d'y accéder pour le regarder ou l'évaluer. 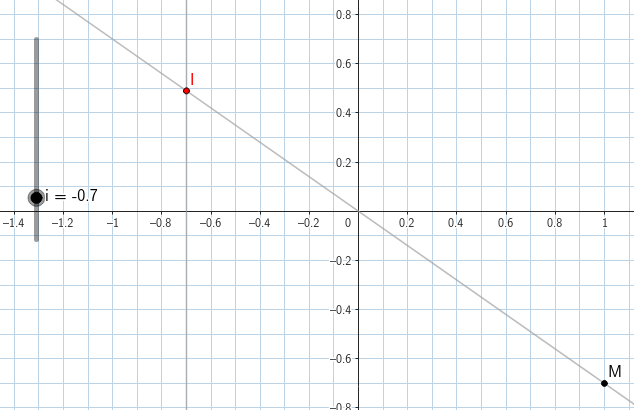:::info Informations Le **curseur** déjà créé, pilote un nombre **`i`** pouvant varier de −1,2 à 1,2. ::: - **Cliquez** avec le bouton droit de la souris sur le quadrillage et utilisez la commande ```Recadrer``` du menu contextuel qui va apparaitre.  - **Créez** en ++noir++ le point M de coordonnées (1 ; i) en saisissant `M=(1,i)` - **Créez** en ++gris clair++ et en ++enlevant++ l'affichage de l'étiquette : - la droite joignant ce point à l'origine par exemple en saisissant `droite(M,(0,0))`. - la droite d'équation $x=i$ en saisissant `x = i`. - **Créez** en ++rouge++ le point I intersection de ces 2 droites et **modifiez** ses propriétés pour en garder la trace en sélectionnant ```Afficher la trace```.  - **Déplacez** lentement le curseur dans toutes les positions possibles. - **Conjecturez** la fonction qui est représentée par la courbe passant par tous les points rouges. - **Regardez** les coordonnées de I pour différentes valeurs de i. - Vous pouvez saisir des procédés de calcul pour **essayer**, puis les effacer si cela ne convient pas. - Dans *Géogebra*, x est la variable par défaut. - Par exemple, la saisie `3x+2` créé la représentation graphique de la fonction $x \mapsto 3x+2$. - **Démontrez** que les coordonnées du point I sont bien de la forme $(i, g(i))$ où $g$ est la fonction précédemment trouvée.