580 views
--- tags: magie, binaire, de bruijn title: magie de bruijn type: slide autoSlide: 10 slideOptions: defaultTiming: 20 transition: slide progress: true parallaxBackgroundImage: "https://minio.apps.education.fr/codimd-prod/uploads/upload_25d71d4a53ee4179f1c2ba27f2393f7d.jpg " --- # magie de bruijn https://codimd.apps.education.fr/p/XUZu6h6KT --- # magie de bruijn * Placer les cartes dans cet ordre: * 8:diamonds:,9:heart:,R:heart:,7:heart:,10:diamonds:,V:clubs:,D:heart:,9:diamonds:, * V:spades:,V:heart:,9:clubs:,7:clubs:,D:diamonds:,10:heart:,9:spades:,R:clubs:, * D:clubs:,R:spades:,10:clubs:,R:diamonds:,8:heart:,As:diamonds:,8:spades:,D:spades:, * 7:diamonds:,7:spades:,As:spades:,8:clubs:,V:diamonds:,10:spades:,As:heart:,As:clubs: <!-- .element: class="fragment" --> --- # magie de bruijn * demander à qq1 de couper le jeu, distribuer 5 cartes <!-- .element: class="fragment" --> * demander qui à du rouge <!-- .element: class="fragment" --> * et déduisez alors leur carte. <!-- .element: class="fragment" --> * [LE MAGICIEN EST ICI](https://codimd.apps.education.fr/p/hos16bfbA#/) --- aide ![](https://minio.apps.education.fr/codimd-prod/uploads/upload_a5ede023a6bc6b3c90e85121b8b58a2c.png =10x) --- # indice ![](https://minio.apps.education.fr/codimd-prod/uploads/upload_c176a8718567e6ab22c2a7fbf734102b.png) --- # Astuce: Pour le collier de 32 perles ci-dessus, fournir une suite de 5 couleurs de perle permet de se positionner de façon unique au sein du collier. --- [Tour avec 8 cartes](https://hal.inria.fr/hal-01383665/file/slides-me%CC%81diation-graphes-algorithmes-Dorian-Mazauric.pdf#page=128) ![](http://images.math.cnrs.fr/IMG/png/8collier-carte.new.png) :+1: ![](http://images.math.cnrs.fr/IMG/png/8config-2.new.png) ![](http://images.math.cnrs.fr/IMG/png/8collier2.new.png) :-1: why? --- <iframe width="1300" height="800" src="https://hal.inria.fr/hal-01383665/file/slides-me%CC%81diation-graphes-algorithmes-Dorian-Mazauric.pdf#page=129" > </iframe> --- [Tour avec 16 cartes](https://www.apmep.fr/IMG/pdf/Atelier_D29.pdf#page=9) --- Par exemple, pour Σ = {a, b, c} et n = 2, m = abacbbcca est un **mot de de Bruijn** puisqu’il contient une unique fois chaque mot de longueur 2 sur Σ, le mot ’aa’ étant obtenu par circularité de m --- # 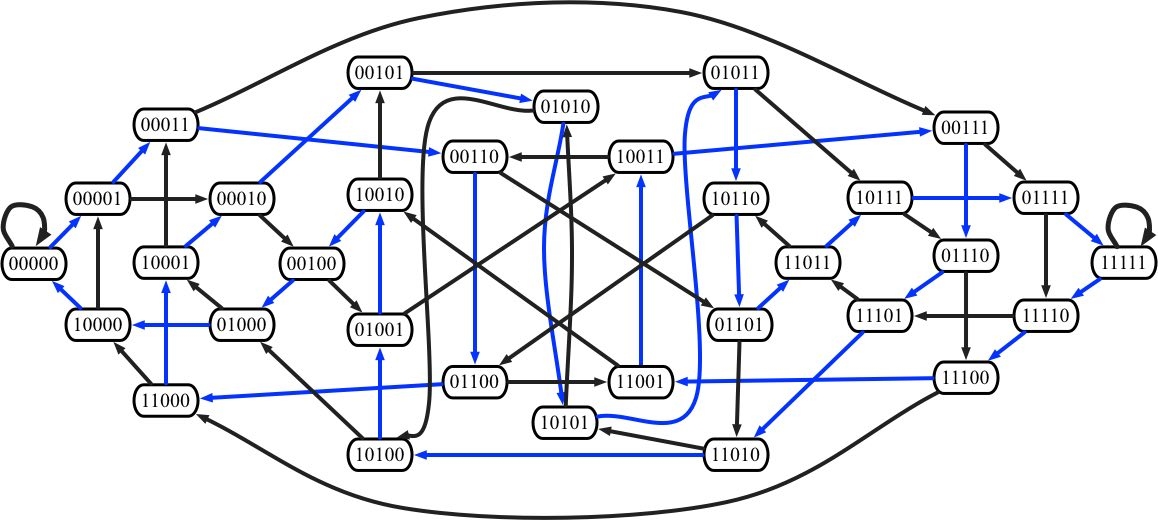graphe de De Bruijn quelle significations peut-on donné aux flèches noires et bleues? 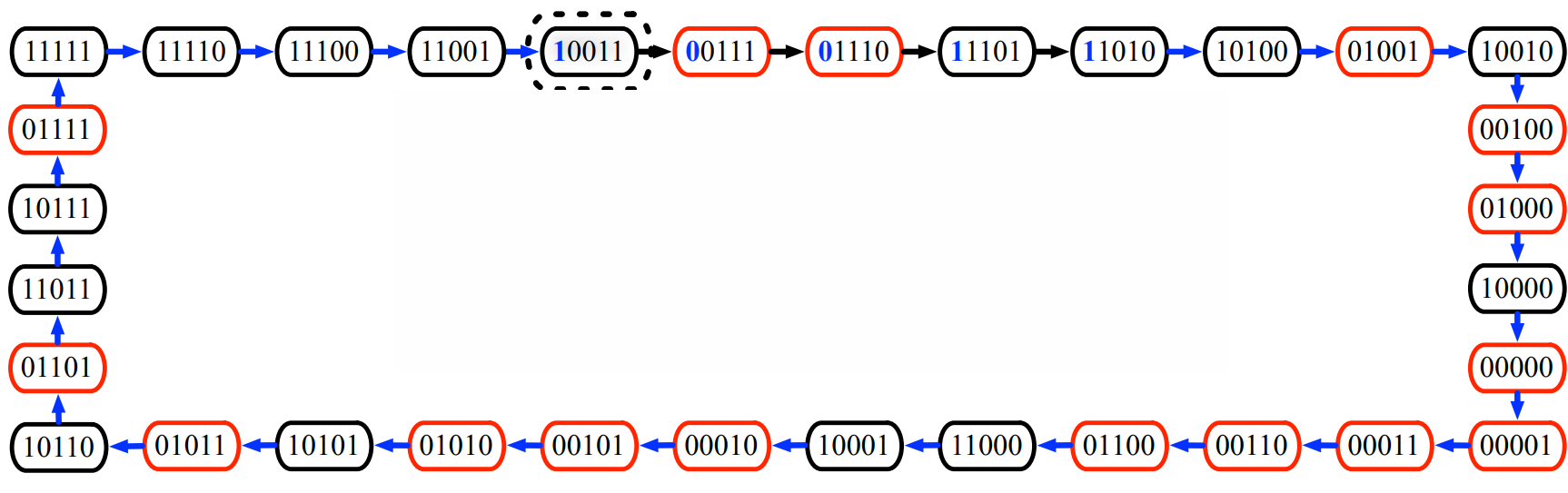![](https://minio.apps.education.fr/codimd-prod/uploads/upload_b2fa6e77a11bfd2923377c0acb526933.png) --- # graphe de De Bruijn en suivant les flèches bleues précédentes, on a un circuit hamiltonien qui passe par toutes les sommets ![](https://minio.apps.education.fr/codimd-prod/uploads/upload_ae3217362f82e481648ad1c608858e8b.png) --- # application : DIGICODE On a encore oublié ce fichu code de la porte d’entrée. Quel est le moyen le plus rapide de trouver le bon code ? --- ## Exemple 1 : digicode avec 2 symboles (0,1) de longueurs 3 - Il y a 8 mots de longueur 3 différents qui sont : 000,001,010,011,100,101,110,111 - Si l’on veut trouver une chaîne de caractère qui contient tous les mots de longueur 3 on peut coller bout à bout tous les mots. - Exemple : Dans l’exemple cela donne par exemple 000001010011100101110111 de longueur $3\times 2^3=24$ ---- ## Exemple 1 : digicode avec 2 symboles (0,1) de longueurs 3 - La longueur la plus petite possible d’une chaine de caractère qui contiendrait tous les mots serait que **les mots se chevauchent** : - les 2 derniers caractères du ième mot seraient égaux aux 2 premiers caractères du (i+1)ème mot. ---- ## Exemple 1 : digicode avec 2 symboles (0,1) de longueurs 3 - Dans ce cas là, chaque mot de conterait que pour 1 nouveau caractère dans la chaine, à part le premier mot qu’il faudrait écrire entièrement. - On aurait donc une taille théorique minimale de $3+(2^3-1)\times 1=10$ caractères - (le 1er mot compte pour 3 caractères les autres comptent uniquement pour 1 caractère). 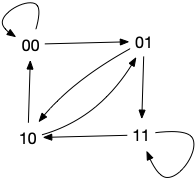--- ## Exemple 1 : digicode avec 2 symboles (0,1) de longueurs 3 Sauf qu’on ne sait pas si un tel mot existe… ni comment le construire ![](https://minio.apps.education.fr/codimd-prod/uploads/upload_6390ca557e3788bb45780a64b15603ab.png) [1011100010](https://www.wikiwand.com/fr/Suite_de_de_Bruijn) [Merci Euler ](https://image.jimcdn.com/app/cms/image/transf/none/path/s58876f6a460c21b5/image/i1c64cabc8b2e761a/version/1412003523/image.jpg) --- ## Exemple 2 : digicode à 4 chiffres x =100x) [lien](https://www.institut-pandore.com/plus/deviner-code-dun-interphone-grace-aux-suites-de-de-bruijn/),[sol](https://tempsdereaction.wordpress.com/2020/03/01/compromis-temps-memoire/#:~:text=pour%20un%20digicode,0100020003000400050006000700080009001100120013001400150016001700180019002100220023002400250026002700280029003100320033003400350036003700380039004100420043004400450046004700480049005100520053005400550056005700580059006100620063006400650066006700680069007100720073007400750076007700780079008100820083008400850086008700880089009100920093009400950096009700980099010102010301040105010601070108010901110112011301140115011601170118011901210122012301240125012601270128012901310132013301340135013601370138013901410142014301440145014601470148014901510152015301540155015601570158015901610162016301640165016601670168016901710172017301740175017601770178017901810182018301840185018601870188018901910192019301940195019601970198019902020302040205020602070208020902110212021302140215021602170218021902210222022302240225022602270228022902310232023302340235023602370238023902410242024302440245024602470248024902510252025302540255025602570258025902610262026302640265026602670268026902710272027302740275027602770278027902810282028302840285028602870288028902910292029302940295029602970298029903030403050306030703080309031103120313031403150316031703180319032103220323032403250326032703280329033103320333033403350336033703380339034103420343034403450346034703480349035103520353035403550356035703580359036103620363036403650366036703680369037103720373037403750376037703780379038103820383038403850386038703880389039103920393039403950396039703980399040405040604070408040904110412041304140415041604170418041904210422042304240425042604270428042904310432043304340435043604370438043904410442044304440445044604470448044904510452045304540455045604570458045904610462046304640465046604670468046904710472047304740475047604770478047904810482048304840485048604870488048904910492049304940495049604970498049905050605070508050905110512051305140515051605170518051905210522052305240525052605270528052905310532053305340535053605370538053905410542054305440545054605470548054905510552055305540555055605570558055905610562056305640565056605670568056905710572057305740575057605770578057905810582058305840585058605870588058905910592059305940595059605970598059906060706080609061106120613061406150616061706180619062106220623062406250626062706280629063106320633063406350636063706380639064106420643064406450646064706480649065106520653065406550656065706580659066106620663066406650666066706680669067106720673067406750676067706780679068106820683068406850686068706880689069106920693069406950696069706980699070708070907110712071307140715071607170718071907210722072307240725072607270728072907310732073307340735073607370738073907410742074307440745074607470748074907510752075307540755075607570758075907610762076307640765076607670768076907710772077307740775077607770778077907810782078307840785078607870788078907910792079307940795079607970798079908080908110812081308140815081608170818081908210822082308240825082608270828082908310832083308340835083608370838083908410842084308440845084608470848084908510852085308540855085608570858085908610862086308640865086608670868086908710872087308740875087608770878087908810882088308840885088608870888088908910892089308940895089608970898089909091109120913091409150916091709180919092109220923092409250926092709280929093109320933093409350936093709380939094109420943094409450946094709480949095109520953095409550956095709580959096109620963096409650966096709680969097109720973097409750976097709780979098109820983098409850986098709880989099109920993099409950996099709980999111121113111411151116111711181119112211231124112511261127112811291132113311341135113611371138113911421143114411451146114711481149115211531154115511561157115811591162116311641165116611671168116911721173117411751176117711781179118211831184118511861187118811891192119311941195119611971198119912121312141215121612171218121912221223122412251226122712281229123212331234123512361237123812391242124312441245124612471248124912521253125412551256125712581259126212631264126512661267126812691272127312741275127612771278127912821283128412851286128712881289129212931294129512961297129812991313141315131613171318131913221323132413251326132713281329133213331334133513361337133813391342134313441345134613471348134913521353135413551356135713581359136213631364136513661367136813691372137313741375137613771378137913821383138413851386138713881389139213931394139513961397139813991414151416141714181419142214231424142514261427142814291432143314341435143614371438143914421443144414451446144714481449145214531454145514561457145814591462146314641465146614671468146914721473147414751476147714781479148214831484148514861487148814891492149314941495149614971498149915151615171518151915221523152415251526152715281529153215331534153515361537153815391542154315441545154615471548154915521553155415551556155715581559156215631564156515661567156815691572157315741575157615771578157915821583158415851586158715881589159215931594159515961597159815991616171618161916221623162416251626162716281629163216331634163516361637163816391642164316441645164616471648164916521653165416551656165716581659166216631664166516661667166816691672167316741675167616771678167916821683168416851686168716881689169216931694169516961697169816991717181719172217231724172517261727172817291732173317341735173617371738173917421743174417451746174717481749175217531754175517561757175817591762176317641765176617671768176917721773177417751776177717781779178217831784178517861787178817891792179317941795179617971798179918181918221823182418251826182718281829183218331834183518361837183818391842184318441845184618471848184918521853185418551856185718581859186218631864186518661867186818691872187318741875187618771878187918821883188418851886188718881889189218931894189518961897189818991919221923192419251926192719281929193219331934193519361937193819391942194319441945194619471948194919521953195419551956195719581959196219631964196519661967196819691972197319741975197619771978197919821983198419851986198719881989199219931994199519961997199819992222322242225222622272228222922332234223522362237223822392243224422452246224722482249225322542255225622572258225922632264226522662267226822692273227422752276227722782279228322842285228622872288228922932294229522962297229822992323242325232623272328232923332334233523362337233823392343234423452346234723482349235323542355235623572358235923632364236523662367236823692373237423752376237723782379238323842385238623872388238923932394239523962397239823992424252426242724282429243324342435243624372438243924432444244524462447244824492453245424552456245724582459246324642465246624672468246924732474247524762477247824792483248424852486248724882489249324942495249624972498249925252625272528252925332534253525362537253825392543254425452546254725482549255325542555255625572558255925632564256525662567256825692573257425752576257725782579258325842585258625872588258925932594259525962597259825992626272628262926332634263526362637263826392643264426452646264726482649265326542655265626572658265926632664266526662667266826692673267426752676267726782679268326842685268626872688268926932694269526962697269826992727282729273327342735273627372738273927432744274527462747274827492753275427552756275727582759276327642765276627672768276927732774277527762777277827792783278427852786278727882789279327942795279627972798279928282928332834283528362837283828392843284428452846284728482849285328542855285628572858285928632864286528662867286828692873287428752876287728782879288328842885288628872888288928932894289528962897289828992929332934293529362937293829392943294429452946294729482949295329542955295629572958295929632964296529662967296829692973297429752976297729782979298329842985298629872988298929932994299529962997299829993333433353336333733383339334433453346334733483349335433553356335733583359336433653366336733683369337433753376337733783379338433853386338733883389339433953396339733983399343435343634373438343934443445344634473448344934543455345634573458345934643465346634673468346934743475347634773478347934843485348634873488348934943495349634973498349935353635373538353935443545354635473548354935543555355635573558355935643565356635673568356935743575357635773578357935843585358635873588358935943595359635973598359936363736383639364436453646364736483649365436553656365736583659366436653666366736683669367436753676367736783679368436853686368736883689369436953696369736983699373738373937443745374637473748374937543755375637573758375937643765376637673768376937743775377637773778377937843785378637873788378937943795379637973798379938383938443845384638473848384938543855385638573858385938643865386638673868386938743875387638773878387938843885388638873888388938943895389638973898389939394439453946394739483949395439553956395739583959396439653966396739683969397439753976397739783979398439853986398739883989399439953996399739983999444454446444744484449445544564457445844594465446644674468446944754476447744784479448544864487448844894495449644974498449945454645474548454945554556455745584559456545664567456845694575457645774578457945854586458745884589459545964597459845994646474648464946554656465746584659466546664667466846694675467646774678467946854686468746884689469546964697469846994747484749475547564757475847594765476647674768476947754776477747784779478547864787478847894795479647974798479948484948554856485748584859486548664867486848694875487648774878487948854886488748884889489548964897489848994949554956495749584959496549664967496849694975497649774978497949854986498749884989499549964997499849995555655575558555955665567556855695576557755785579558655875588558955965597559855995656575658565956665667566856695676567756785679568656875688568956965697569856995757585759576657675768576957765777577857795786578757885789579657975798579958585958665867586858695876587758785879588658875888588958965897589858995959665967596859695976597759785979598659875988598959965997599859996666766686669667766786679668766886689669766986699676768676967776778677967876788678967976798679968686968776878687968876888688968976898689969697769786979698769886989699769986999777787779778877897798779978787978887889789878997979887989799879998888988998989999000) il faudrait en principe tester toutes les 10 000 combinaisons, de longueur totale 40 000. En utilisant une suite de de Bruijn, il suffit de taper au plus 10 003 chiffres (les 3 derniers pour facteur qui chevauche le début). --- # Travail de recherche {%slideshare mrchretien/histoiredigicodepdf %} https://fr.slideshare.net/mrchretien/histoiredigicodepdf --- # source: * https://cahier-de-prepa.fr/mp-charlemagne/download?id=365 * https://dridk.me/assemblage.html * images.math.cnrs.fr/La-magie-des-colliers-de-perles-de-Nicolaas-Govert-de-Bruijn.html * https://hal.inria.fr/hal-01383665/file/slides-me%CC%81diation-graphes-algorithmes-Dorian-Mazauric.pdf? --- # source 2: * https://www.wikiwand.com/fr/Suite_de_de_Bruijn * https://sm2g.github.io/de-bruijn-sequencer/ * https://capes-nsi.org/pdf/2020/2020_epreuve_1.pdf * https://capes-nsi.org/pdf/2020/2020_epreuve_1_correction.pdf * https://irem.univ-reunion.fr/spip.php?article1076 * http://www.maths-pour-tous.org/cours-mej/doc/Dossier%20MeJ%202010-14/Dossier%20Mej%20%202011-12/Digicode/Rapport%20Groupe%20Digicodes%20final.pdf