# Correction de l'évaluation non-notée : Périmètre et aire
<img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_faf29600e4c9f0f03beea09eb00178c4.png" alt="Image" style="display: block; margin-left: auto; margin-right: auto; width: 15%;">
## Exercice 1 - Périmètres et aires de figures simples
1. a. $\textrm{Périmètre}_{CATS}=4+6+4+6=20\,\textrm{cm}$
b. $\textrm{Périmètre}_{\mathscr{C}}=2\times{}pi\times{}rayon$
$=2\times{}\pi\times3=6\pi\,\textrm{cm}$
c. $\textrm{Périmètre}_{LYNX}=5+7+5+7=24\,\textrm{cm}$
d. $\textrm{Périmètre}_{DOG}=5+6+5=16\,\textrm{cm}$
2. a. $Aire_{CATS}=Longueur\times{}largeur$
$=4\,\textrm{cm}\times6\,\textrm{cm}=24\,\textrm{cm}^2$
b. $Aire_{disque}=\pi\times{}rayon^2$
$=\pi\times(3\,\textrm{cm})^2=9\pi\,\textrm{cm}^2$
c. $Aire_{LYNX}=base\times{}hauteur$
$=7\,\textrm{cm}\times4\,\textrm{cm}=28\,\textrm{cm}^2$
d. $Aire_{DOG}=\dfrac{base\times{}hauteur}{2}$
$=\dfrac{6\,\textrm{cm}\times4\,\textrm{cm}}{2}=12\,\textrm{cm}^2$
## Exercice 2 - Une surface de jardin
1. a. L'aire du **terrain** est constitué :
- d'un rectangle de $20\,\textrm{m}$ de longueur et $10\,\textrm{m}$ de largeur.
- d'un demi-disque de $5\,\textrm{m}$ de rayon
- d'un triangle rectangle à soustraire à cette surface d'une hauteur d'une longueur de $4\,\textrm{m}$ ($10\,\textrm{m}-6\,\textrm{m}=4\,\textrm{m}$) et d'une base d'une longueur de $3\,\textrm{m}$
($20\,\textrm{m}-17\,\textrm{m}=3\,\textrm{m}$).
$Aire_{terrain}=Aire_{rectangle}+Aire_{1/2-disque}-Aire_{triangle}$
$=20\,\textrm{m}\times10\,\textrm{m}+\dfrac{\pi\times(5\,\textrm{m})^2}{2}+\dfrac{3\,\textrm{m}\times4\,\textrm{m}}{2}$
$=200\,\textrm{m}^2+\dfrac{25\pi}{2}\,\textrm{m}^2+6\,\textrm{m}^2\approx233{,}25\,\textrm{m}^2$
L'aire du terrain est de $233{,}25\,\textrm{m}^2$.
b. $Aire_\textrm{maison}=11\,\textrm{m}\times6\,\textrm{m}=66\,\textrm{m}^2$
L'aire de la maison est de $66\,\textrm{m}^2$.
c. $Aire_{jardin}=Aire_{terrain}-Aire_{maison}$
$Aire_\textrm{jardin}\approx233{,}25\,\textrm{m}^2-66\,\textrm{m}^2=167{,}25\,\textrm{m}^2$
L'aire du jardin est de $167{,}25\,\textrm{m}^2$.
2. a. Un sac de gazon permet de couvrir une surface de $40\,\textrm{m}^2$. On calcule donc :
$\dfrac{167,25}{40}\approx4{,}18\,\textrm{sacs}$
Ainsi, il faudra alors $5\,\textrm{sacs}$ à M. Mat Grass pour qu'il puisse couvrir l'ensemble de son jardin.
b. Un sac coûte $12{,}50\,\textrm{€}$. On calcule :
$12{,}50\times5=62{,}50\,\textrm{€}$
Finalement, M. Mat Grass devra payer $62{,}50\,\textrm{€}$.
## Exercice 3 - Des cirques et des fractions
1. Proportion de fauves au cirque Pandor : $\dfrac{5}{12}$
Proportion de fauves au cirque Zopoutou : $\dfrac{11}{24}$
2. Pour comparer deux fractions, on les écrit sous le même dénominateur et on a :
$\dfrac{5}{12}=\dfrac{5\times}{12\times2}=\dfrac{10}{24}<\dfrac{11}{24}$
La proportion de fauve est donc plus importante au cirque Zopoutou qu'au cirque Pandor.
## Exercice 4
1. 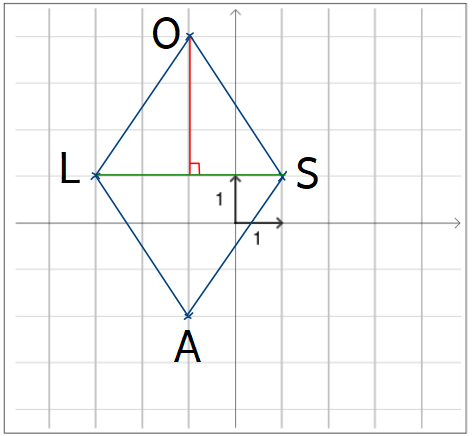
2. On peut partager le losange en deux triangles de d'aire égale, on peut donc calculer l'aire d'un premier triangle et la multiplier par $2$.
$Aire_{LOS}=\dfrac{base\times{}hauteur}{2}=\dfrac{4\times3}{2}=6\,\textrm{u.a.}$
$Aire_{LOSA}=2\times{}Aire_{LOS}=2\times6=12\,\textrm{u.a.}$
<style>
body {
background-color: #f7f9fb;
color: #454545;
font-family: Arial, sans-serif;
}
h1 {
color: #ff7979; /* Rouge pastel */
}
h2 {
color: #74b9ff; /* Bleu pastel */
}
h3 {
color: #55efc4; /* Vert pastel */
}
h4 {
color: #fab1a0; /* Orange pastel */
}
h5,
h6 {
color: #454545; /* Couleur par défaut pour les titres de niveau inférieur */
}
a {
color: #8b90af;
}
hr {
border-color: #dcdcdc;
}
blockquote {
background-color: #f2f2f2;
border-left: 4px solid #dcdcdc;
color: #555555;
padding: 10px;
margin: 10px 0;
}
code {
background-color: #f5f7fa;
border: 1px solid #e1e5eb;
color: #777777;
padding: 2px 4px;
}
pre {
background-color: #f5f7fa;
border: 1px solid #e1e5eb;
color: #777777;
padding: 10px;
overflow: auto;
}
table {
border-collapse: collapse;
width: 100%;
}
th, td {
border: 1px solid #dcdcdc;
padding: 8px;
}
th {
background-color: #f2f2f2;
}
td {
background-color: #ffffff;
}
</style>