--- title: Olympiades de mathématiques 2025 - Pour aller plus loin. tags: OLY, 2025 ---  # Olympiades 2025 - Pour aller plus loin :::info <i class="fa fa-info-circle fa-2x fa-pull-left "></i> Cette page s'adresse aux professeurs de mathématiques. Elle se veut être un complément au sujet des Olympiades de mathématiques pour le plaisir de faire des mathématiques et donner des idées d'activités avec les élèves. [Lien vers la page académique des Olympiades avec les sujets <i class="fa fa-external-link" aria-hidden="true"></i>](https://pedagogie.ac-orleans-tours.fr/spip.php?article1701). ::: [toc] ## Peut-on obtenir une distribution uniforme pour la somme de deux dés truqués ? On sait bien que la somme 7 est la plus probable en lançant deux dés, plus précisément, la distribution de la somme $S$ est celle donnée ci-dessous. | Somme $s_i$ | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |-----------|----|----|----|----|----|----|----|----|----|----|----| | $P(S=s_i)$ | $\frac{1}{36}$ | $\frac{2}{36}$ | $\frac{3}{36}$ | $\frac{4}{36}$ | $\frac{5}{36}$ | $\frac{6}{36}$ | $\frac{5}{36}$ | $\frac{4}{36}$ | $\frac{3}{36}$ | $\frac{2}{36}$ | $\frac{1}{36}$ | Dans l'exercice 3 de l'épreuve académique 2025 on se demandait si en truquant un dé et en le lançant deux fois on pouvait obtenir une somme qui suive une distribution uniforme sur ⟦2;12⟧. La réponse est négative. On peut alors se demander si c'est possible avec deux dés différents. Ce problème a été inspiré du problème de février 2010 de la [Centrale des Maths](https://centraledesmaths.uregina.ca/mp/previous2009/feb10sol.php). :::success **Problème** On se demande s'il est possible de truquer deux dés à six faces numérotées de 1 à 6 de sorte que les différentes sommes de 2 à 12 soient équiprobables. ::: Soient $p_1,\dots,p_6$ les probabilités associées aux faces du premier dé et $q_1,\dots,q_6$ celles du second dé. On note $S$ la variable aléatoire correspondant à la somme des points des deux dés. ### Expérimentation avec GeoGebra Sur l'applet ci-dessous vous pouvez faire varier les valeurs des $p_i$ et des $q_i$ en déplaçant les points en forme de triangles noirs [ <i class="fa fa-caret-right" aria-hidden="true"></i> ] et observer la distribution de la somme $S$. <iframe scrolling="no" title="Distribution de la somme de deux dés truqués" src="https://www.geogebra.org/material/iframe/id/eyqkbqzz/width/720/height/437/border/888888/sfsb/true/smb/false/stb/false/stbh/false/ai/false/asb/false/sri/false/rc/false/ld/false/sdz/false/ctl/false" width="720px" height="437px" style="border:0px;"> </iframe> En expérimentant, il semble impossible de trouver une solution. En particulier, pour que les sommes de 2 et de 12 atteignent une probabilité de $\frac{1}{11}$, il faut que $p_1$ et $q_1$ ainsi que $p_6$ et $q_6$ soient assez élevés mais alors il semble que la probabilité de $S=7$ soit toujours bien trop grande. Cela nous donne une stratégie pour une démonstartion. [L'applet GeoGebra est en ligne ici <i class="fa fa-external-link" aria-hidden="true"></i>](https://www.geogebra.org/m/j5r9yrgh) ### Démonstration Pour que la somme des dés suive une distribution uniforme, il est en particulier nécessaire que : $$P(S=2) = P(S=12) = \frac{1}{11}.$$ Nous allons montrer la propriété suivante de deux manières avec des pistes différentes. :::info **Propriété** Si $P(S=2) = P(S=12) = \frac{1}{11}$, alors $P(S=7)>\frac{1}{11}$. ::: On suppose que $P(S=2) = P(S=12) = \frac{1}{11}$, soit : $$p_1q_1 = \frac{1}{11} \quad \text{et}\quad p_6q_6 = \frac{1}{11}.$$ Pour la somme $S=7$, nous avons : $$P(S=7) = p_1q_6 + p_2q_5 + p_3q_4 + p_4q_3 + p_5q_2 + p_6q_1.$$ Donc : $$\boxed{P(S=7) \geqslant p_1q_6 + p_6q_1.}\quad (*)$$ ### Preuve n°1 -- Avec l'inégalité arithmético-géométrique ==[N.B. cette idée de preuve a été fournie par ChatGPT]== Appliquons dans $(*)$ l'inégalité arithmético-géométrique aux réels positifs $p_1q_6$ et $p_6q_1$ : $$p_1q_6 + p_6q_1 \geq 2\sqrt{p_1q_6 \cdot p_6q_1}.$$ Or, nous savons que : $$p_1q_6 \cdot p_6q_1 = (p_1q_1)(p_6q_6) = \frac{1}{11} \times \frac{1}{11} = \frac{1}{121}.$$ Donc on a la minoration : $$p_1q_6 + p_6q_1 \geq 2\sqrt{\frac{1}{121}} = \frac{2}{11}.$$ Ainsi : $$P(S=7)\geqslant \frac{2}{11}.$$ :::warning <i class="fa fa-check-square-o fa-3x fa-pull-left" aria-hidden="true"></i> Ainsi $P(S=2) = P(S=12) = \frac{1}{11} \implies P(S=7)>\frac{1}{11}$ ce qui prouve qu'il est impossible d'obtenir une distribution uniforme sur ⟦2;12⟧ de la somme $S$ de deux dés dont les faces sont exactement $\{1,2,3,4,5,6\}$. ::: ### Preuve n°2 -- En utilisant une fonction On repart de : $$p_1q_1 = \frac{1}{11} \quad \text{et}\quad p_6q_6 = \frac{1}{11}.$$ On a donc : $$q_1 = \frac{1}{11p_1} \quad \text{et}\quad q_6 = \frac{1}{11p_6}.$$ Ce qui donne : $p_1q_6 + p_6q_1 = p_1\times \frac{1}{11p_6} + p_6\times \frac{1}{11p_1} =\frac{1}{11}\left( \frac{p_1}{p_6}+\frac{p_6}{p_1}\right)$ Dans $(*)$, la minoration $P(S=7) \geqslant p_1q_6 + p_6q_1$ devient donc : $$ P(S=7) \geqslant \frac{1}{11}\left( \frac{p_1}{p_6}+\frac{p_6}{p_1}\right) $$ Notons $x=\frac{p_1}{p_6}$. Pour conclure, il suffit de prouver le lemme suivant : :::info **Lemme** Quel que soit le réel strictement positif $x$ on a : $$x+\frac1x >1.$$ ::: Plusieurs approches sont possibles pour prouver ce lemme : #### 2.1 -- Méthode algébrique. Pour tout $x$ strictement positif, $x+\frac1x >1$ équivaut (en multipliant par $x$) à $x^2+1 >x$, soit encore : $$x^2-x+1 >0$$ ##### 2.1.1 Etude du polynôme $x^2-x+1$. Pour établir cette dernière inégalité on peut considérer le polynôme du second degré $x\longmapsto x^2-x+1$ qui admet un minimum sur $\mathbb{R}$ en $\frac12$ qui vaut $\frac14-\frac12+1=\frac34>0$. ##### 2.1.2 Avec une identité remarquable. On peut aussi remarquer que pour tout $x$ réel : $$x^2-x+1 = (x^2-2x+1) +x= (x-1)^2+x$$ Pour tout $x$ strictement positif, la somme $(x-1)^2+x$ est aussi strictement positive, ce qui permet de conclure. Une autre méthode consiste à prouver que la fonction $f:x\longmapsto x+\frac1x$ admet un minimum de 2 sur $]0;+\infty[$, ce qui est fait ci-dessous. #### 2.2 -- Etude de la fonction $f:x\longmapsto x+\frac1x$ sur $]0;+\infty[$. La fonction $f$ est dérivable sur $]0;+\infty[$ et on a : $$f'(x)=1-\frac{1}{x^2}=\frac{x^2-1}{x^2}=\frac{(x-1)(x+1)}{x^2}$$ On dresse le tableau de signes de ce quotient pour obtenir que $f$ admet sur $]0;+\infty[$ un minimum en 1 qui vaut $f(1)=2$. Ainsi, pour tout $x$ strictement positif, on a $x+\frac1x \geqslant 2$. --- On a ainsi prouvé que $P(S=7) \geq \frac{1}{11}\left( \frac{p_1}{p_6}+\frac{p_6}{p_1}\right)$ et donc via le lemme que : $$ P(S=7) > \frac{1}{11} $$ On a même vu avec la preuve **2.2** (comme la preuve **1**) que $P(S=7) \geqslant \frac{2}{11}$ :::warning <i class="fa fa-check-square-o fa-3x fa-pull-left" aria-hidden="true"></i> Ainsi $P(S=2) = P(S=12) = \frac{1}{11} \implies P(S=7)>\frac{1}{11}$ ce qui prouve qu'il est impossible d'obtenir une distribution uniforme sur ⟦2;12⟧ de la somme $S$ de deux dés dont les faces sont exactement $\{1,2,3,4,5,6\}$. ::: :::info **Remarque.** On peut interpréter différemment "truquer les dés", par exemple en changeant les nombres apparaissant sur les faces, tout en gardant les dés équilibrés. Une astuce possible est alors de numéroter les faces d'un dé 0, 2, 4, 6, 8, 10, et celles de l'autre dé avec les numéros 1 et 2 répétés trois fois chacun. On voit immédiatement que les douze sommes de 1 à 12 sont alors équiprobables. Si on obtient une somme de 1, on doit relancer 😎. ::: --- ## Complément au sujet des tresses : Nœuds et Polynômes d'Alexander ### Introduction Un des objectifs de la théorie des tresses (et de celles des nœuds que nous évoquerons ensuite) est de pouvoir **distinguer** et **classer** les objets étudiés dans la théorie. Dans le sujet d'olympiade de cette année (2025), nous avons abordé le *codage des tresses* et *le théorème d'Artin*. La combinaison des deux nous a permis de prouver l'équivalence de tresses. La suite logique est de trouver, via des algorithmes, des tresses de plus en plus simples équivalentes à une tresse donnée. C'est le principe de **l'algorithme des réductions de poignées**. Dans ce complément, nous allons explorer une autre voie, celle des *nœuds* et du *polynôme de Jones*. ### Les nœuds et entrelacs Un _nœud_ en mathématiques est une corde fermée (qui n’a pas de bout) (voir la figure 1). Un _entrelacs à deux composantes_ est formé de deux cordes fermées , un _entrelacs à trois composantes_ est formé de trois cordes fermées (voir la figure 2), etc... | 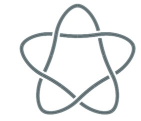 | 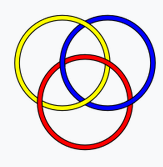 | | ------------------------------------ | --------------------------------------------- | | Nœud ou<br>Entrelac à 1 composante | Entrelac à 3 composantes <br> (Anneaux Borroméens) | > A partir d’une tresse on peut construire un entrelac (ou un nœud) en reliant les bouts de la tresse entre eux (fermeture) comme dans la figure ci-dessous. Un tel entrelac s’appelle une _tresse fermée_. Alexander a démontré que tout entrelacs peut être obtenu de la sorte. 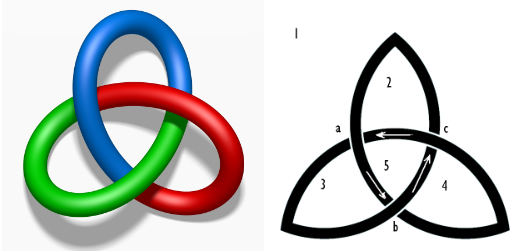(source : https://images-archive.math.cnrs.fr/Les-tresses-de-la-topologie-a-la-cryptographie.html) > |  |  | | --------------------- | :-----------------------: | | Tresse à 4 brins | Entrelacs à 4 composantes | **Autre exemple** : la fermeture de la tresse ci-dessous permet d'obtenir le nœud de trèfle |  |  | | ------------------------------------ | ------------------------------------ | | Tresse | Noeud de trèfle | **Tresses, jonglage et entrelacs** Les figures de jonglage se modélisent par des tresses en regardant les balles vues du dessus et en déroulant leurs positions dans le temps. Le jonglage classique à trois balles se modélise ainsi par la tresse habituelle à trois brins (dessus, dessous) et dont la fermeture forme les anneaux borroméens.  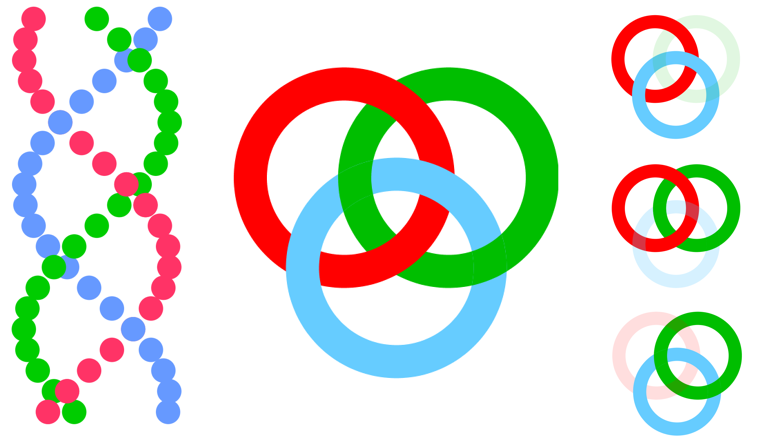La dernière figure montre la non transitivité de la relation "*est au dessus de*" (notée ">") dans les anneaux borroméens (ou la tresse) : 🔵>🔴 et 🔴>🟢 mais 🟢>🔵. ### Polynôme d'Alexander > Le **polynôme d'Alexander** est un [invariant de nœuds](https://fr.wikipedia.org/wiki/Invariant_de_n%C5%93uds) qui associe un polynôme à coefficients entiers à chaque type de nœud. C'est le premier [polynôme de nœud (en)](https://en.wikipedia.org/wiki/Knot_polynomial "en:Knot polynomial") découvert ; il l'a été par [James Waddell Alexander II](https://fr.wikipedia.org/wiki/James_Waddell_Alexander_II "James Waddell Alexander II"), en 1923. > (Source : Wikipedia) Le calcul d'un polynôme de nœuds nous permettra, en théorie, de distinguer deux nœuds qui ne sont pas équivalents. En effet, si deux nœuds sont équivalents, alors leurs polynômes de nœuds seront égaux. Nous nous servirons en particulier de la contraposée de cette propriété, si deux nœuds ont des polynômes différents, alors ils ne seront pas équivalents. Attention, il n'y a pas équivalence, deux nœuds ayant les mêmes polynômes d'Alexander ne seront pas forcément équivalents. Nous en reparlerons à la fin de document. #### Diagramme de partage On appellera diagramme associé à un nœud une projection régulière du nœud sur le plan, avec comme informations supplémentaires : lorsque que deux arêtes du diagramme se croisent, on sait laquelle des deux est au-dessus de l’autre dans l’espace. De plus on sait dans quel sens on parcourt le nœud.  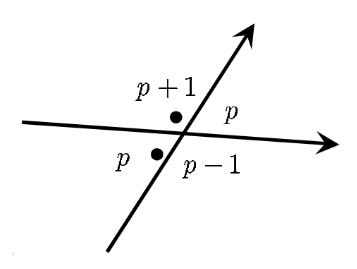Lorsque l’on a le diagramme d’un nœud, il s’agit tout d’abord de l’orienter, c’est à dire, en s’imaginant marcher le long du diagramme : savoir dans quel sens le parcourir, et arrivé à un point de croisement, savoir quelle est l’arête du dessus et quelle est celle du dessous. Nous allons adopter les notations d’Alexander. À chaque croisement du diagramme, on adoptera la notation suivante : deux régions consécutives vont être pointées au niveau de chaque croisement, de telle sorte que si on se déplace sur l’arête passant "en dessous", on ait les deux régions pointées sur notre gauche. Il faut noter que dans le cas d’un nœud simple, il suffit d’orienter un point de croisement du nœud pour avoir l’orientation complète de celui-ci et de son diagramme en suivant l’arête orientée comme telle. Pour un entrelacs il sera nécessaire d’orienter une arête de chaque composante. Il s’agit maintenant de donner ce qu’on appellera un index (un entier relatif) aux différentes régions du diagramme de la manière suivante : on choisit une région au hasard à laquelle on attribue l’index 0 ; ensuite, les régions devront être indexées de façon à ce que lorsque l’on passe d’une région à une autre en traversant une arête de droite à gauche, orientation déterminée par celle de l’arête, on baisse d’un index.  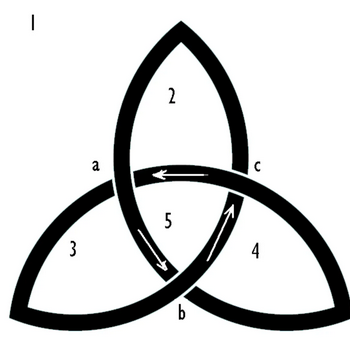Cette indexation donne lieu donne lieu à la propriété suivante : :::warning **Propriété :** Soit $n$ un entier naturel et un diagramme de nœuds à $n$ points de croisement. Le diagramme délimite alors exactement $n + 2$ régions du plan. ::: :::success **Preuve** : La formule d’Euler pour les polyèdres donne que le nombre de sommets $s$, de faces $f$ et d’arêtes $a$ vérifient la relation : $s − a + f = 2$. En regardant le diagramme comme un graphe non orienté dont les sommets sont les points de croisement, on s’aperçoit qu’on a : $a = 2s$. En effet, de chaque point de croisement, il y a 4 arêtes qui en partent. Chaque arête étant comptée 2 fois, à chacun de ses sommets, on a : $$a = \frac12 (4s)$$ Donc on a finalement : $−s + f = 2$. D’où le résultat. ::: #### Matrice d'incidence Considérons un diagramme orienté du nœud avec $n$ croisements ; le diagramme partage le plan en $n + 2$ régions. Pour déterminer le polynôme d'Alexander, on construit d'abord une matrice d'incidence de taille $(n, n + 2)$. Les $n$ rangées correspondent aux $n$ croisements, et les $n+ 2$ colonnes aux régions. Considérons l'entrée correspondant à une région et à un croisement particulier. Si la région n'est pas adjacente au croisement, cette entrée vaut 0. Sinon, la table suivante donne la valeur de l'entrée compte tenu de la position de la région vue du point de vue de la ligne entrante passant par dessous l'autre : - à gauche avant le croisement : $−t$ - à droite avant le croisement : $1$ - à gauche après le croisement : $t$ - à droite après le croisement : $−1$ En supprimant alors de la matrice deux colonnes correspondant à des régions adjacentes, on obtient une nouvelle matrice d'ordre $n$ ; son déterminant (à un facteur $t^n$ près) est le polynôme d'Alexander (la forme normalisée est obtenue en choisissant ce facteur de telle sorte que le terme constant du polynôme soit non nul et positif). 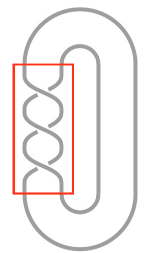##### Exemple : le nœud de trèfle Le calcul correspond au diagramme ci-contre  :  La matrice d'incidence est : $$\begin{pmatrix} -1&1&t &0 & -t \\ -1&t&0&1 & -t \\ -1&0&1&t&-t\\ \end{pmatrix}$$ dont les cinq colonnes correspondent respectivement aux régions 1 à 5, et les trois lignes aux croisements a, b et c. En supprimant les deux dernières colonnes (correspondant aux deux régions adjacentes 4 et 5), on obtient : $$\begin{pmatrix} -1&1&t \\ -1&t&0 \\ -1&0&1 \\ \end{pmatrix}$$ de déterminant $t^2 − t + 1$ ; le polynôme d'Alexander est donc $t^2 − t + 1$. Le même diagramme, en remplaçant le croisement en $a$ par son *opposé* (en échangeant la position respective des brins), donne un nœud trivial (équivalent à un cercle), une matrice d'incidence qui devient : $$\begin{pmatrix} 1&-t&-1 &0 & t \\ -1&t&0&1 & -t \\ -1&0&1&t&-t\\ \end{pmatrix}$$ d'où le calcul du déterminant de : $$\begin{pmatrix} 1&-t&-1 \\ -1&t&0 \\ -1&0&1 \\ \end{pmatrix}$$ égal à $-t$ et finalement le polynôme d'Alexander trivial 1. ### Conclusion #### Limites Le calcul du polynôme de d'Alexander ne permet pas de distinguer tous les nœuds. En effet, un nœud et son nœud réfléchi (en inversant tous les nœuds) ont les même polynôme de d'Alexander. C'est aussi le cas avec le nœud inversé (le même nœud parcouru dans l'autre sens). ### Ouverture D'autres méthodes ont ainsi été développées, parmi elles : - [polynôme de Jones](https://fr.wikipedia.org/wiki/Polyn%C3%B4me_de_Jones "Polynôme de Jones"), - le polynôme HOMFLY, - le [groupe fondamental](https://fr.wikipedia.org/wiki/Groupe_fondamental "Groupe fondamental") du [complément d'un nœud](https://fr.wikipedia.org/wiki/Compl%C3%A9ment_d%27un_n%C5%93ud "Complément d'un nœud"), - les [invariants de type fini](https://fr.wikipedia.org/w/index.php?title=Invariant_de_Vassiliev&action=edit&redlink=1 "Invariant de Vassiliev (page inexistante)") de [Vassiliev](https://fr.wikipedia.org/wiki/Victor_Anatolyevich_Vassiliev "Victor Anatolyevich Vassiliev") … #### Applications Les théories des tresses et celle de nœuds ont eu des applications dans des domaines tels que : - la **cryptographie** Dans le système de cryptage proposé dans [[KoAl-00](https://images-archive.math.cnrs.fr/Les-tresses-de-la-topologie-a-la-cryptographie.html#KoAl-00)] la clé privée d’Alice est la donnée de deux tresses, γ1 et γ2, et sa clé publique est une troisième tresse α accompagnée de la composition γ1αγ2. Pour que ce système soit fiable, il faut qu’il n’y ait pas d’algorithme rapide pour résoudre l’équation XαY=β, où α et β sont des tresses données, et X et Y sont des variables. - l'**ADN** et son entrelac des deux brins en hélice. Certaines enzymes (DNAses) coupent les brins d'ADN et d'autres (ligases) permettent de les souder. Il existe aussi des topoisomérases qui sont des enzymes qui contrôlent la structure topologique de l’ADN en générant des coupures transitoires, avant de les refermer pour limiter les sur-enroulements. - La **chimie des polymères** - Le jonglage (cf [conférence d'ouverture aux JNAPMEP 2023](https://youtu.be/lX1A382Czho?feature=shared) par Vincent Pantaloni).