--- tags : Introduction, Équation, Second degré, Première spé --- <center>  </center> # Une résolution carrée >« Je suis l'équation triste : au bras d'une inconnue. » >[name=Léo FERRÉ] > ## Calcul mental 1. Pouvez-vous **trouver** deux nombres tels que leur somme soit $3$ et leur produit $2$ ? 🖋 Si oui, recopiez et complétez la phrase : ::: success … et … sont deux nombres de somme $3$ et de produit $2$. ::: 2. Pouvez-vous **trouver** deux nombres tels que leur somme soit $9$ et leur produit $20$ ? 🖋 Si oui, recopiez et complétez la phrase : ::: success … et … sont deux nombres de somme $9$ et de produit $20$. ::: 3. Pouvez-vous **trouver** deux nombres tels que leur somme soit $1$ et leur produit $-6$ ? 🖋 Si oui, recopiez et complétez la phrase : ::: success … et … sont deux nombres de somme $1$ et de produit $-6$. ::: 4. Pouvez-vous **trouver** deux nombres tels que leur somme soit $20$ et leur produit $96$ ? 🖋 Si oui, recopiez et complétez la phrase : ::: success … et … sont deux nombres de somme $20$ et de produit $96$. ::: 5. Pouvez-vous **trouver** deux nombres tels que leur somme soit $1$ et leur produit $-1$ ? 🖋 Si oui, recopiez et complétez la phrase : ::: success … et … sont deux nombres de somme $1$ et de produit $-1$. ::: ## Équation 1 - Comme nous ne sommes pas sûrs d'avoir toutes les réponses possibles aux questions précédentes, nous allons essayer d'être plus rigoureux en utilisant **deux inconnues** $x$ et $y$. - 🖋 **Écrivez** le système de deux équations correspondant à la somme vaut $3$ et le produit vaut $2$. - 🖋 **Utilisez** l'équation provenant de la somme pour isoler une des deux inconnues. - 🖋 **Remplacez** alors cette inconnue par son autre écriture dans l'équation du produit. - 🖋 **Savez-vous** résoudre cette dernière équation ? - Si oui, faites-le - Sinon, connaissez-vous une méthode de résolution où seule une étape vous bloque ? ## Diophante à la rescousse <center>  Diophante</center> :::info On ne connaît pas avec certitude l’époque où **Diophante** vécut. Sans doute était-ce aux alentours de 250 de notre ère. :::spoiler *Un peu plus* - Vous avez peut-être lu son nom dans vos livres de mathématiques, qui proposent souvent la résolution d’une équation construite à partir de l’inscription qui aurait été gravée sur sa tombe[^Dio] [^Dio]: Selon un livre de « Récréations mathématiques » du 17e siècle, voici l’épitaphe qui **aurait été** gravée sur la tombe de Diophante : *Les chiffres diront la durée de sa vie. Sa douce enfance en fait le sixième Un douzième de sa vie a passé Et son menton s’est couvert de duvet. Marié, il a vécu le septième de sa vie sans enfant. Cinq ans ont encore passé ; la naissance d’un fils l’a rendu heureux. Le sort a voulu que la vie de ce fils soit deux fois plus courte que celle de son père. Plein de tristesse, le vieillard a rendu l’âme quatre ans après la mort de son fils. Dis, passant, quel âge avait atteint Diophante lorsque la mort l’a enlevé ?* - *Diophante* est connu dans le monde des mathématiciens, essentiellement par ses treize livres d’arithmétiques dont six seulement sont parvenus jusqu’à nous. Cette œuvre influença les algébristes arabes, ceux de la renaissance européenne et les plus grands mathématiciens, dont Fermat (1601-1665), qui écrivit en marge de la traduction qu’il en possédait, ce qui est devenu le grand théorème de Fermat, qui vient d’être démontré il y a peu. - ***Les Arithmétiques*** sont une série de petits problèmes, accompagnés de leur solution, où l’on cherche des nombres (rationnels positifs), vérifiant certaines conditions. ::: Voici un extrait de ses **Arithmétiques** : :::success **Problème XXVII**[^Ext] [^Ext]: Exrait issu de : Diophante, Les six livres d’arithmétique et le livre des nombres polygones, traduction P. ver Eecke , Blanchard, Paris, 1959.] *Trouver deux nombres tels que leur somme et leur produit forment des nombres donnés. Il faut toutefois que le carré de la demi-somme des nombres à trouver excède d’un carré le produit de ces nombres ;* Proposons donc que la somme des nombres forme 20 unités, et que leur produit forme 96 unités. ::: Ainsi il y a 18 siècles, *Diophante* s'était posé notre quatrième question et l'avait résolu ainsi : :::success Que l’excédent des nombres soit 2 arithmes. Dès lors, puisque la somme des nombres est 20 unités, si nous la divisons en deux parties égales, chacune des parties sera la moitié de la somme, ou 10 unités. Donc, si nous ajoutons à l’une des parties, et si nous retranchons de l’autre partie, la moitié de l’excédent des nombres, c’est-à-dire 1 arithme, il s’établit de nouveau que la somme des nombres est 20 unités, et que leur excédent est 2 arithmes. En conséquence, posons que le plus grand nombre est 1 arithme augmenté de 10 unités qui sont la moitié de la somme des nombres ; donc le plus petit nombre sera 10 unités moins 1 arithme, et il s’établit que la somme des nombres est 20 unités et que leur excédent est 2 arithmes. Il faut aussi que le produit des nombres forme 96 unités. Or leur produit est 100 unités moins 1 carré d’arithme ; ce que nous égalons à 96 unités, et l’arithme devient 2 unités. En conséquence, le plus grand nombre sera 12 unités, le plus petit sera 8 unités, et ces nombres satisfont à la proposition. ::: À la première lecture, nous sommes un peu perdus. :::warning :::spoiler **Cliquez** ici pour avoir un peu d'**aide** : - L'excédent des deux nombres est l'écart entre les deux nombres. - un arithme est un nombre inconnu. 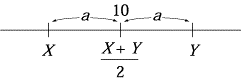Aujourd'hui nous pourrions le remplacer par « inconnue $a$ » - Le début du texte correspond au dessin ci-dessous : :::spoiler dessin <center> </center> ::: - 🖋 **Relisez** le texte et **écrivez** l'équation d'inconnue $a$ correspondant à « *Il faut aussi que le produit des nombres forme 96 unités.* » - 🖋 **Terminez** la résolution de façon moderne en **trouvant** pour $a$ la solution que *Diophante* semble oublier. - 🖋 **Résolvez** à la façon de *Diophante* les questions initiales qui vous résistaient. - Dans l'introduction du problème 27, *Diophante* laisse entendre que le problème pourrait ne pas avoir de solution, puisse qu'il indique qu'une condition est nécessaire. 🖋 **Ecrivez** une question semblable qui n'aurait aucune réponse. ## Et Al-Khwãrizmi complète le carré ### Des informations :::info Quelques siècles après *Diophante*, entre les années 813 et 830 après J.-C. paraît, à Bagdad, un texte qui allait caractériser toute une branche des mathématiques. Ce texte avait pour titre « Kitab al-jabr wa al-muqãbala » dont l’auteur, **Al-Khwãrizmi** (mort en 907 ap. J.-C.), travaillait à la maison de la sagesse de Bagdad, comme mathématicien et astronome. ::: <center>  Al-Khwãrizmi </center> Dans son introduction il précise les objectifs de son ouvrage : >J’ai rédigé, dans le domaine du calcul par le jabr, un abrégé englobant les plus fines et les plus nobles opérations du calcul dont les hommes ont besoin pour la répartition de leurs héritages et de leurs donations, pour leurs partages et pour leurs jugements, pour leurs transactions commerciales et pour toutes les opérations qu’ils ont entre eux, relatives à l’arpentage, à la répartition des eaux des rivières, à l’architecture ainsi qu’à d’autres aspects. (…) > >J’ai découvert aussi que les nombres dont on a besoin dans le calcul par la restauration et la comparaison sont de trois types : ce sont les racines, les carrés et le nombre seul, non rapporté à une racine ni à un carré. > >Parmi eux, la racine est toute chose, le carré est tout ce qui résulte de la racine multipliée par elle-même. Le nombre seul est tout ce qui est exprimé comme nombre sans rapport à une racine ni à un carré. > >[name=Al-Khwãrizmi, *Kitãb al-jabr wa al-muqãbala*, dans^[Djebbar A : Une histoire de la science arabe, Seuil, Paris, 2001, page 223]][color=#3c763d] :::info Le titre de l’ouvrage d’*Al-Khwãrizmi* est tout à la fois une discipline et deux opérations. Il s’agit en fait d’un programme. Une des traductions possibles est : « ***Abrégé du calcul par la restauration et la comparaison*** ». ::: :::warning :::spoiler Cliquez ici pour obtenir un peu de **Vocabulaire** - Le terme ***al-jabr*** - signifie remplissage, rééquilibrage, restauration et vise à transformer, à restaurer, l’équation donnée afin de l’exprimer avec des nombres positifs exclusivement. - a donné le mot ***Algebrista***, qui en espagnol a gardé son sens originel de « rebouteux », celui qui réduit, restaure, une entorse, une fracture. - a également donné le mot ***Algèbre*** qui représente la branche des mathématiques qui en utilisant le calcul avec des lettres, unifie la géométrie et le calcul. - Le terme ***al-muqãbala*** signifie, quant à lui comparaison et désigne le regroupement, dans une équation, des expressions semblables. Ainsi un problème qui s’écrirait algébriquement $3x^2-2x+5=2x^2+4$ subit d’abord l’opération *al-jabr* qui consiste à additionner de part et d’autre de l’égalité $2x$. L’équation est alors « restaurée » (il n’y a plus que des grandeurs positives). Elle devient $3x^2+5=2x^2+2x+4$ . Suit alors l’opération *al-muqãbala* qui consiste en la réduction des termes semblables. L’équation devient $x^2+1=2x$. ::: Dans ce traité Al-Khwãrizmi recense, entre autres, 6 types d’équation du premier ou du second degré auxquels peuvent se rapporter toutes les équations étudiées auparavant que ce soit du temps des Babyloniens, des Grecs, des Séleucides ou de Diophante, à savoir : 1. « Des carrés qui égalent des racines » 2. « Des carrés qui égalent un nombre » 3. « Des racines qui égalent un nombre » 4. « Des carrés et des racines qui égalent un nombre » 5. « Des racines et un nombre qui égalent des carrés » 6. « Des carrés et un nombre qui égalent des racines » ### Des mathématiques Le texte ci-dessous^[Djebbar A : *Une histoire de la science arabe*, Seuil, Paris, 2001, page 324] décrit la démarche adoptée par *Al-Khwãrizmi* pour résoudre une équation de type 4. :::success Un carré et des racines égales à un nombre, c’est comme si l’on disait : un carré et dix racines sont égales à trente-neuf drachmes, dont voici la signification, le carré auquel on ajoute dix fois la racine, donne un total qui est trente neuf. La règle de ce cas est de prendre la moitié des racines, soit cinq. Multipliées en elles-mêmes elles donnent vingt-cinq : en y ajoutant trente-neuf on obtient soixante-quatre. Prenons-en la racine qui est huit. Ensuite enlevons à ce résultat cinq. Il reste trois qui est la racine du carré. Et le carré est neuf. ::: :::warning :::spoiler **Vocabulaire** utile : - Chez *Al-Khwãrizmi* : - La « racine » est le nombre cherché, l'inconnue qu'en notation moderne, nous écrivons $x$. - Le « carré » est le carré de ce nombre inconnu, qu'en notation moderne, nous écrivons $x^2$. - Finalement, comme il s'agit à cette époque de nombre positif, $\sqrt{x^2}=x$ rend une certaine cohérence au nom utilisé. La « racine » est la racine carrée de la surface inconnue d'un carré. - Aujourd'hui la lettre utilisée pour représenter l'inconnue évite de se méprendre sur ce que l'on cherche. - Comme le laisse entendre sa conclusion, *Al-Khwãrizmi* cherche 2 nombres intimement liés, l'aire du carré et son côté. ::: - 🖋 **Écrivez** sous forme moderne l'équation qu'*Al-Khwãrizmi* résoud dans cet exemple. - 🖋 **Vérifiez** que 3 est effectivement solution de cette équation. ### Explications de la méthode Voici un dessin qui va évoluer et éclairer la méthode d'*Al-Khwãrizmi* : - On part d'un carré de côté inconnue $x$. Son aire est $x^2$.  - On va lui adjoindre $10x$ qui est l'aire d'un rectangle de $10$ par $x$. Mais plutôt que de fabriquer un long rectangle, on va partager le rectangle $10x$ en deux rectangles égaux apposés sur 2 côtés consécutifs du carré.  - L'équation dit que la surface obtenue est $39$. - Et on voit également qu'il manque un carré de côté $5$ pour que cette figure devienne un carré.  - Le carré complété de côté … a donc pour surface $39+25=64$. - 🖋 Je vous laisse **terminer** le raisonnement et **trouver** la deuxième solution de l'équation. - 🖋 Saurez-vous **adapter** de façon moderne (on écrivant des équations équivalentes) la méthode d'*Al-Khwãrizmi* pour résoudre - $x^2-2x-3=0$, - $x^2-20x+96=0$ et - $x^2-x-1=0$ ?