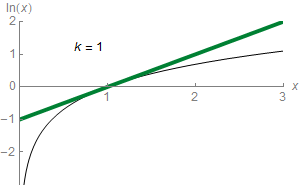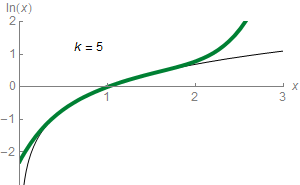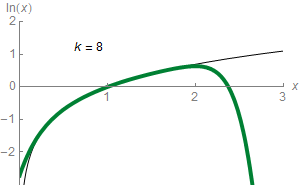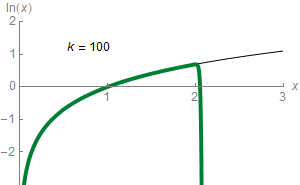
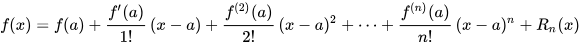
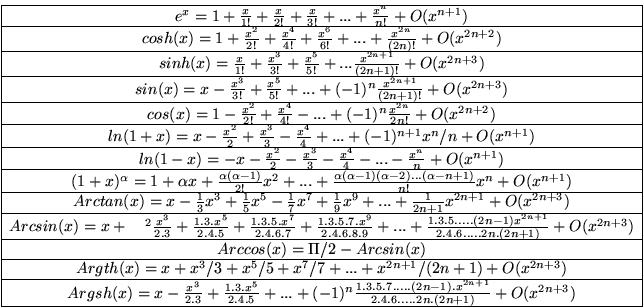
--- tags: fourier, fft, tdf ,transformé title: --- # Transformée de Fourier Discrète https://tinyurl.com/transf-fourier-discrete [pdf élève](https://nuage03.apps.education.fr/index.php/s/mSFyDtRTJFQoke8), [codimd eleve](https://codimd.apps.education.fr/jXwmxQ2iRU2-al1V_HBxhw?view) ## I. Approximation de fonction continue ### 1.par des polynômes :::spoiler    ::: ### 2.par des fonctions trigonométriques :::spoiler Pour des fonctions $f$ périodiques. 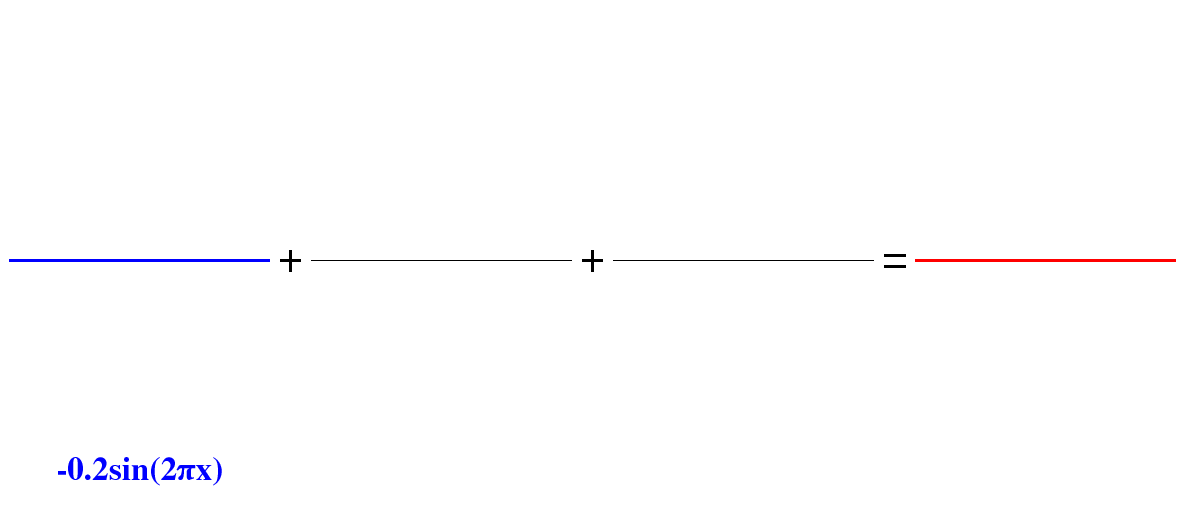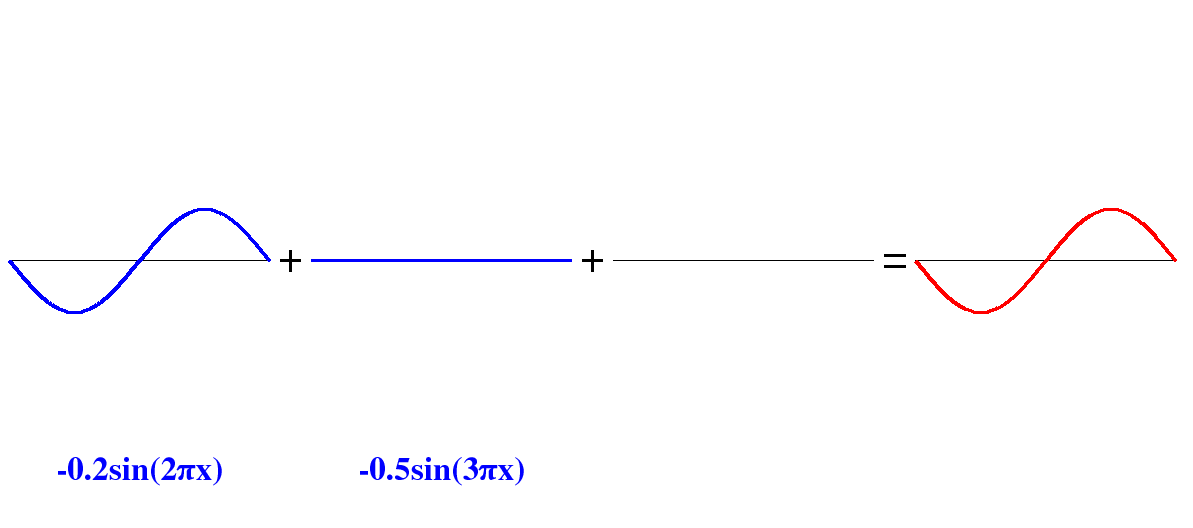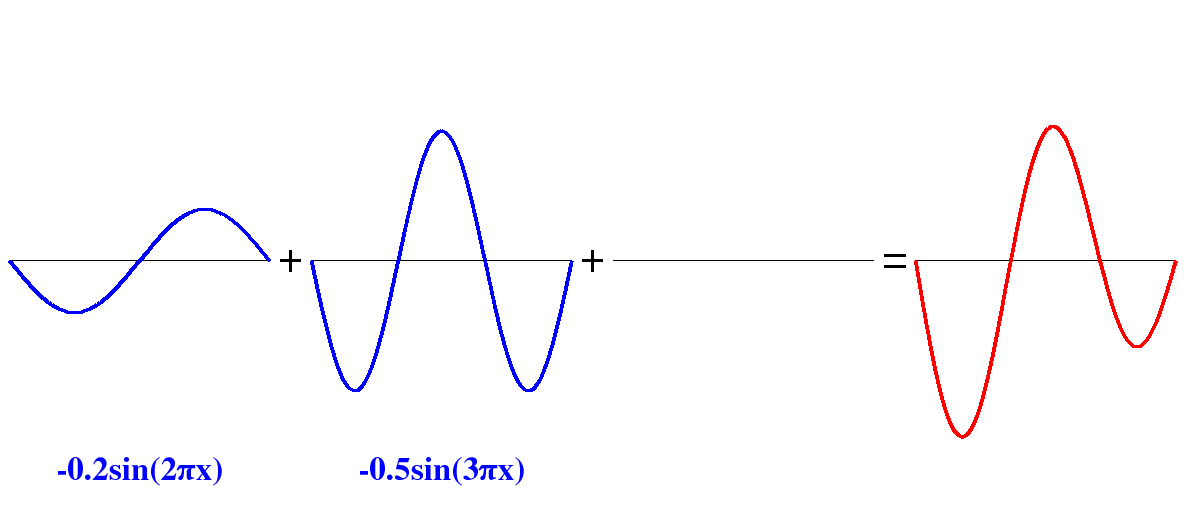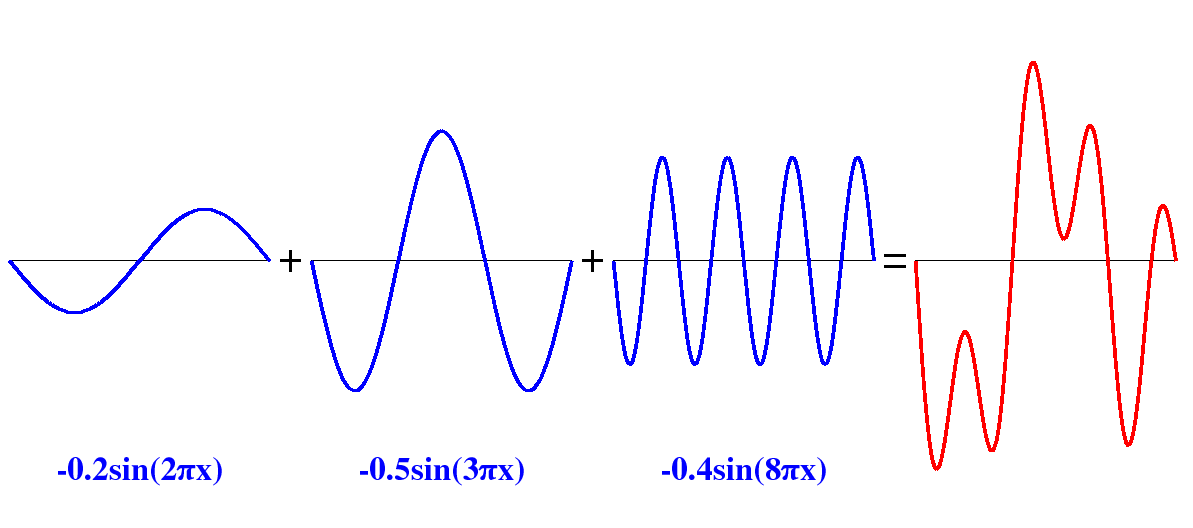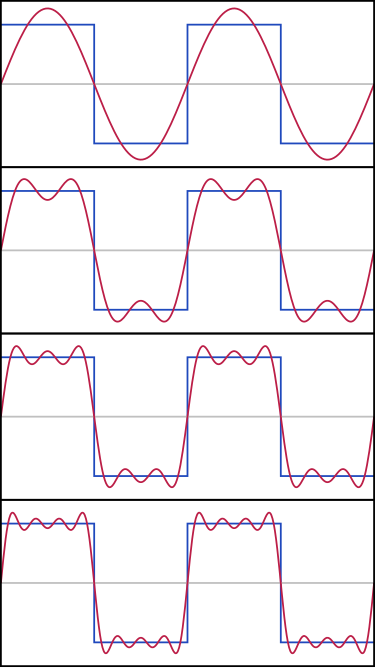$$f(t)\approx a_0(f)+\sum_{n≥1}(a_n(f)cos(nt)+b_n(f)sin(nt))$$ $$f(t)\approx \sum_{n∈Z}c_n(f)e^{int}$$    $$0,19sin(πx) + 0.086sin(3πx) + 0.044sin(5πx) – 0.035sin(7πx) + 0.038sin(9πx) + 0.005sin(11πx) – 0.004sin(13πx) + 0.007sin(15πx) + 0.004sin(17πx) + 0.008sin(19πx) +..$$ [source](https://interstices.info/la-decomposition-en-series-de-fourier/) ::: ## II. 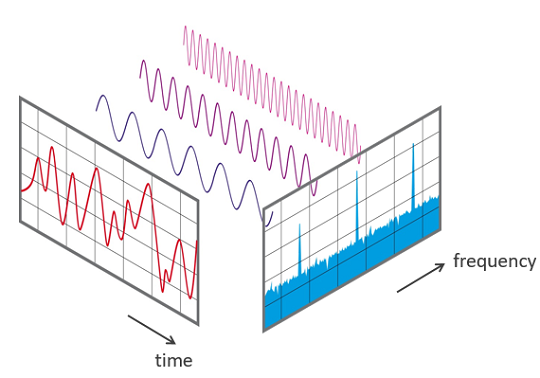La transformée de Fourier  Voici une métaphore en français simple: - Que fait la transformée de Fourier ? A partir d'un smoothie, elle trouve sa recette. - Comment ? Elle passe le smoothie dans un filtre pour en extraire chaque ingrédient. - Pourquoi ? Les recettes sont plus faciles à analyser, comparer et modifier que le smoothie lui-même. - Comment récupérer le smoothie ? Re-mélanger les ingrédients.  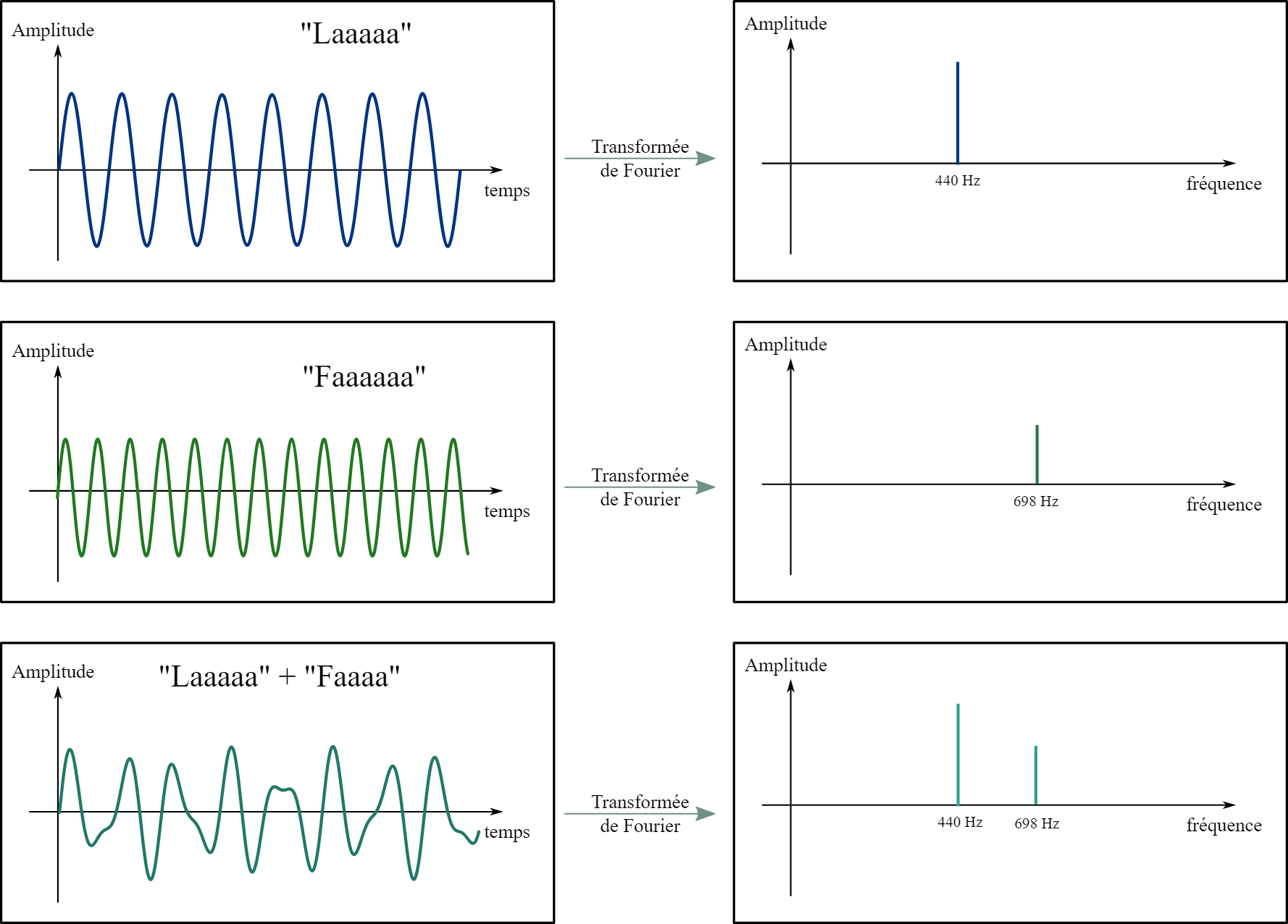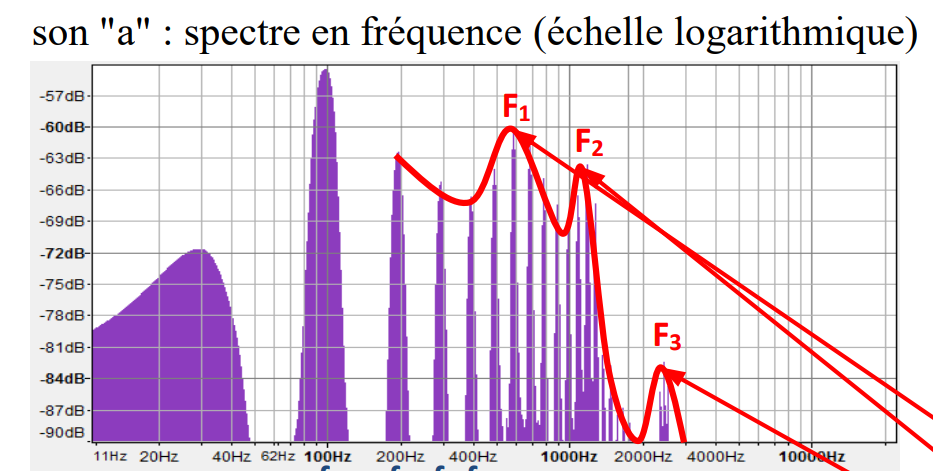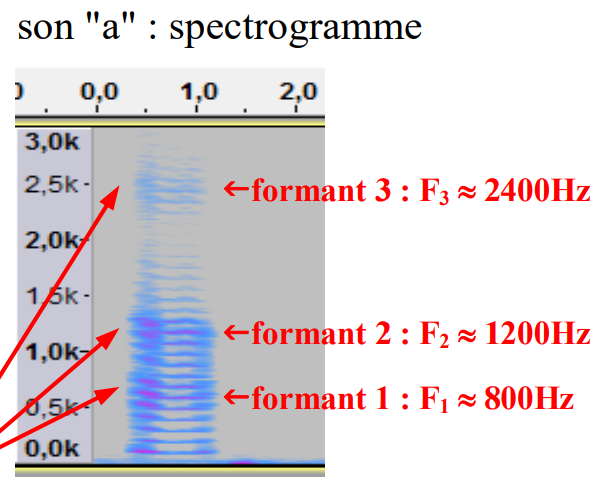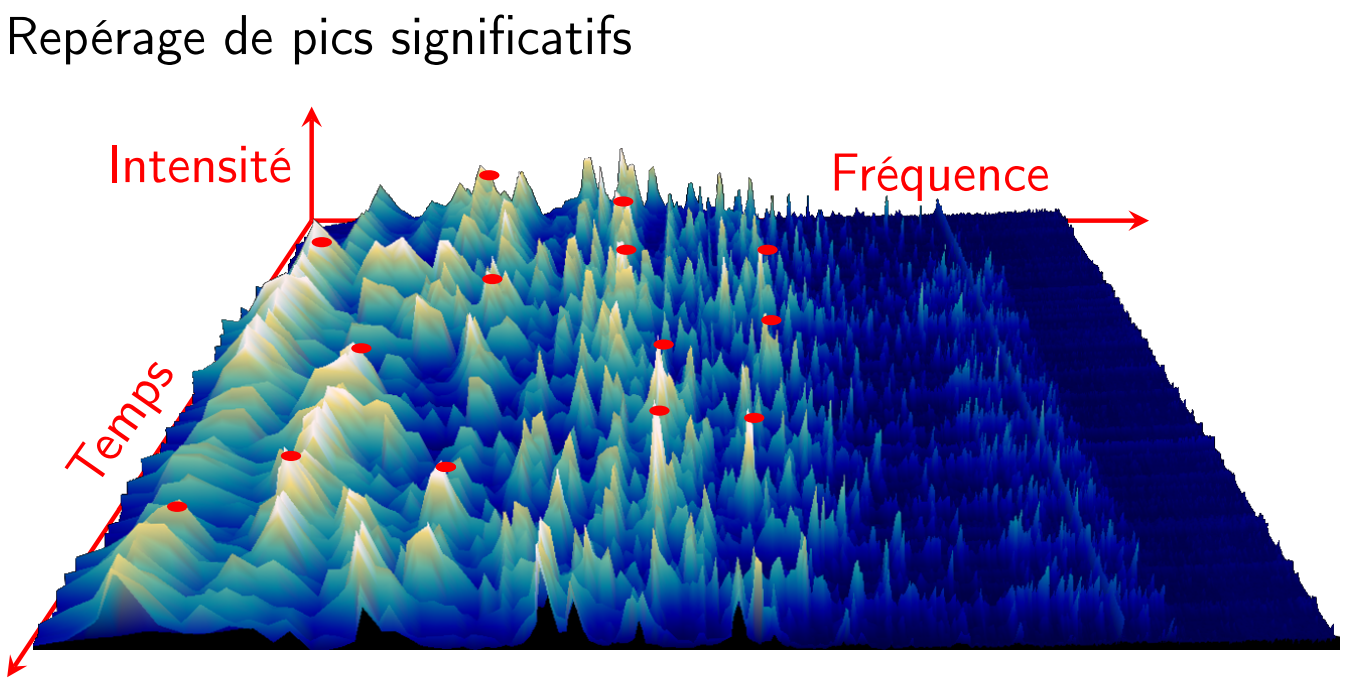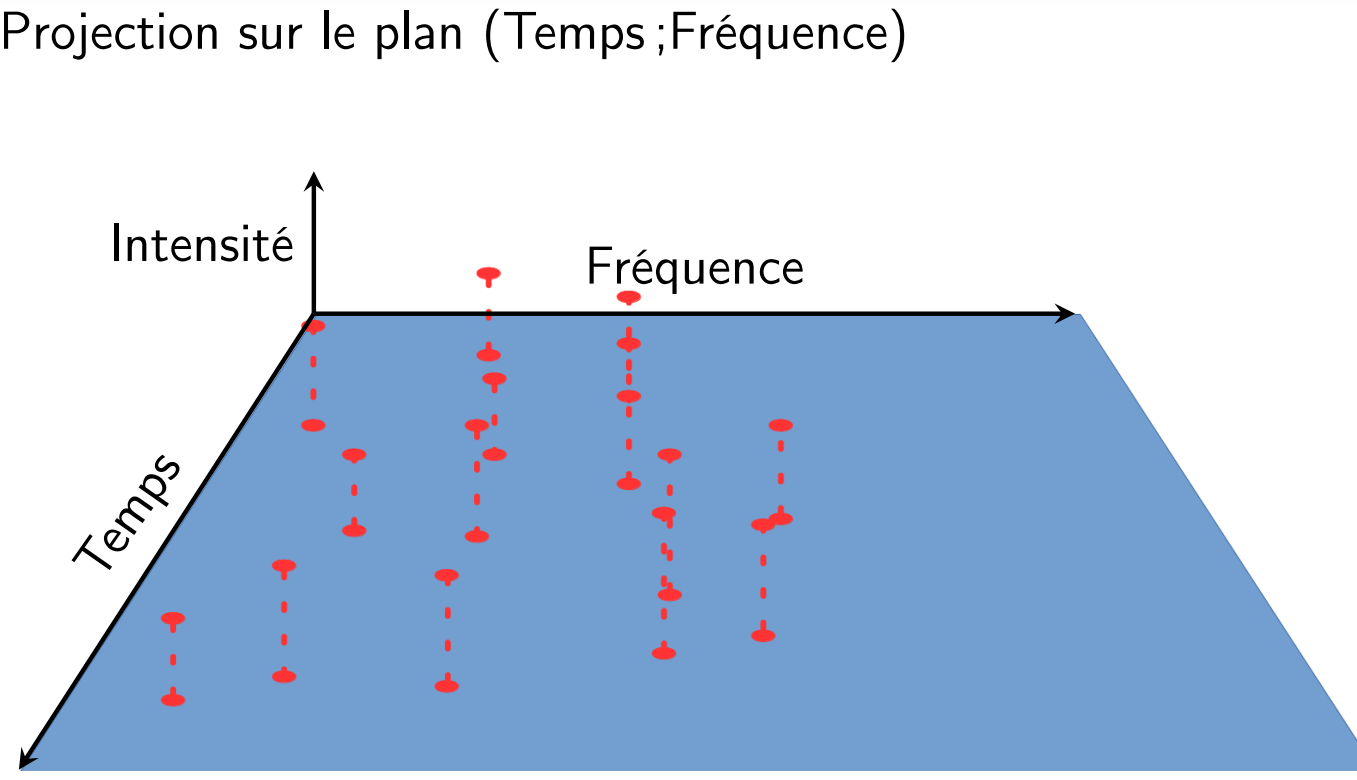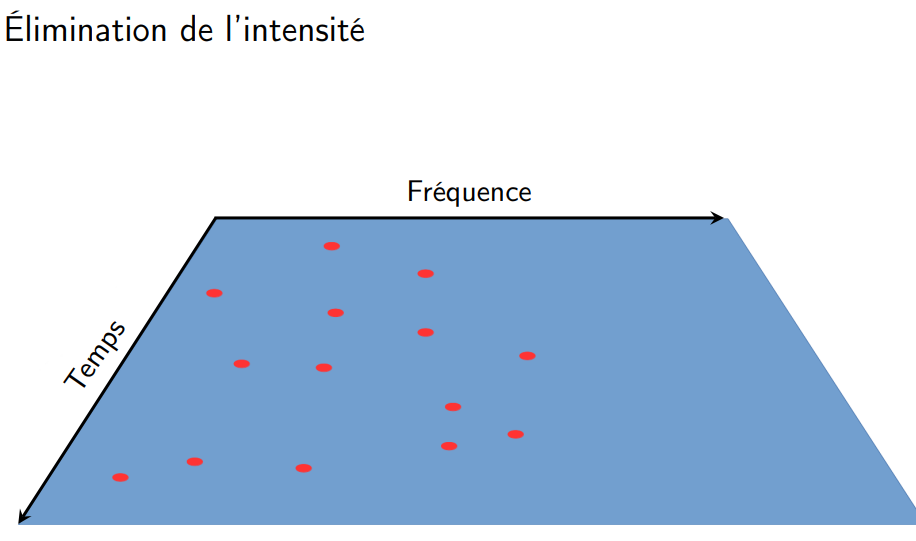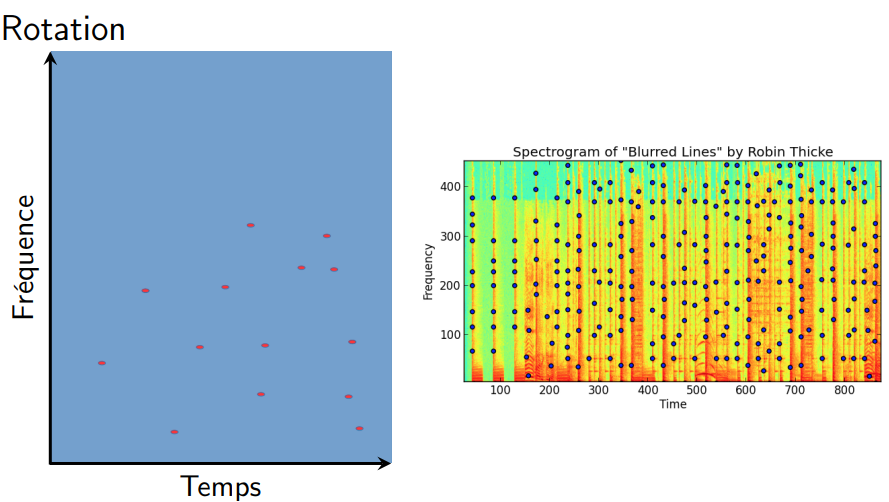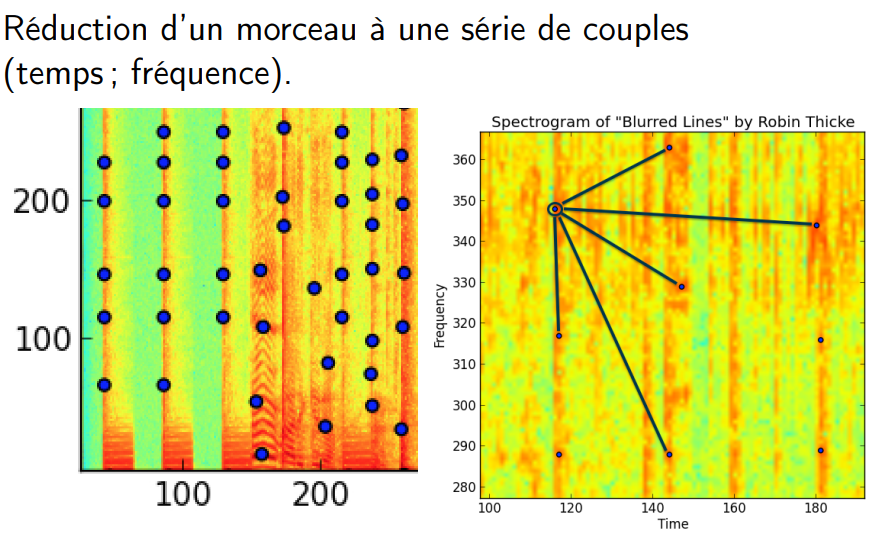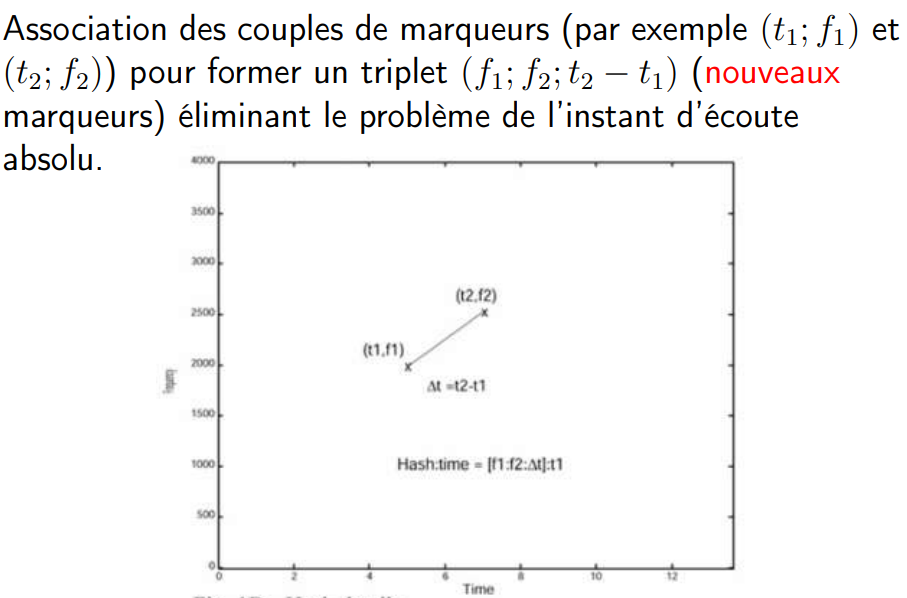**l'idée**: il est plus simple de connaitre les fréquences et leur amplitudes (partie droite ) que toutes les valeurs de la fonction (son ici, partie gauche) :::spoiler **Formants**: reconnaissance voyelle   ::: :::spoiler [**Shazam**](https://irem.univ-poitiers.fr/portail/attachments/article/167/BeamerRegionaleShazam_Site.pdf#page=18)       + Comparaison à une base de données comportant les empreintes de millions de morceaux extraites par ce même algorithme {%youtube En7XJu7cNDM %}à 6'40 ::: ## 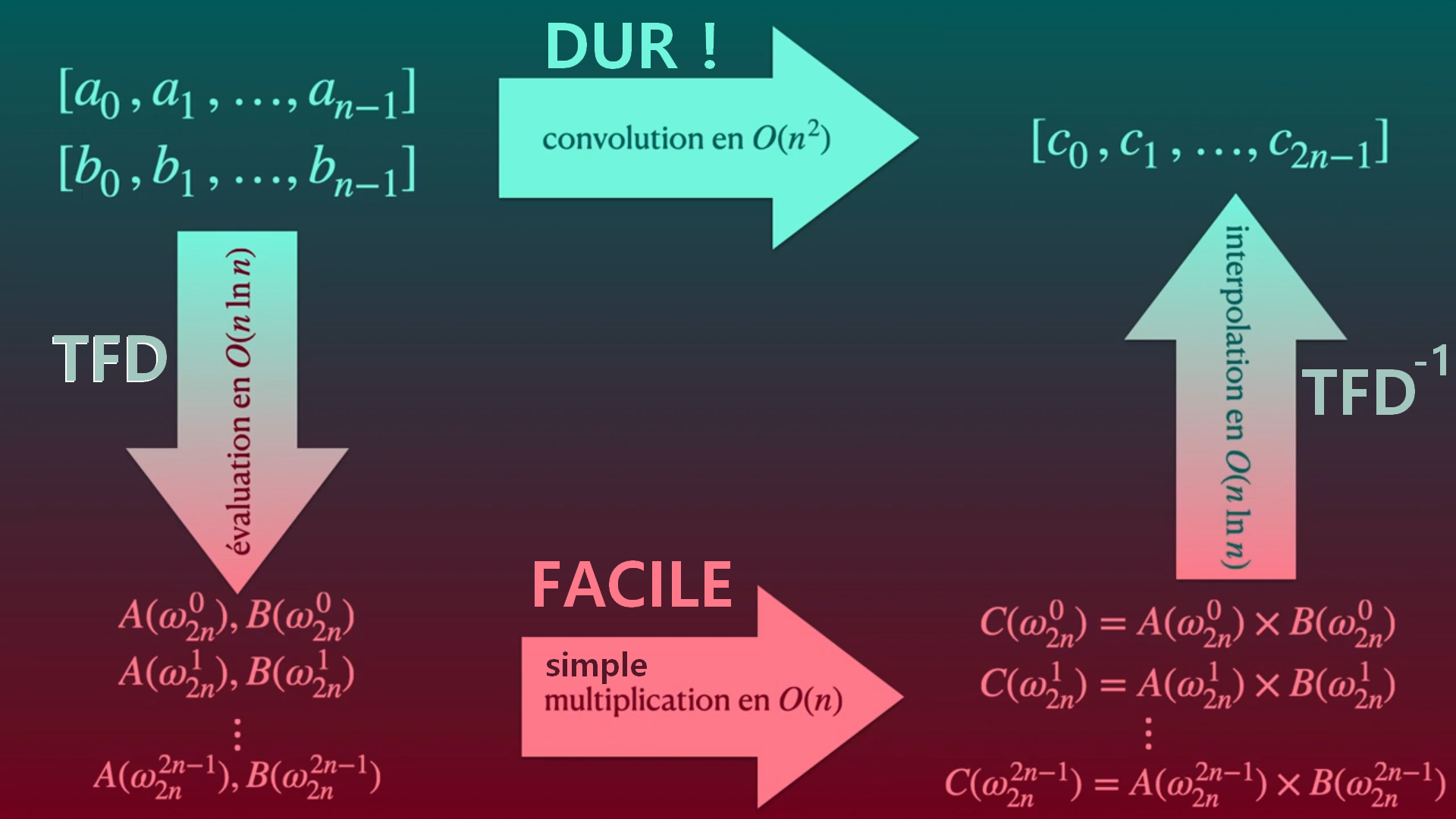III. La Transformée de Fourier Discrète  En informatique, on a un nombre fini de valeurs ,on est en **mode discret** (a contrario dans le monde réel, les signaux analogiques sont en mode continu) **l'idée**: c'est toujours la même: connaitre les fréquences et leur amplitudes plutôt qu'un ensemble finis de valeurs de la fonction . En mode continu, l'outil mathématique sous jacent est la Transformée de Fourier qui utilise des intégrales Ici, en mode discret ,l'outil mathématique est la Transformée de Fourier Discrète qui utilise des sommes. Définissons là: :::warning Soient $x_0,x_1,...,x_{N-1}$ , N valeurs d'un signal discret $x. On a $X$ la Transformée de Fourier de Discrète de $x$ tel que Pour $k = 0, 1, \dots, N-1 \quad$,$$\quad X[k] = \sum_{n=0}^{N-1} x[n] e^{-j \frac{2\pi}{N} kn}$$ En posant $\omega=e^{-j \frac{2\pi}{N}}$, on a $$\quad X[k] = \sum_{n=0}^{N-1} x[n] \omega^ {kn}$$ ::: Rq: $\omega$ est la racine primitive $N$-ième de l'unité : $\quad X[0] = \sum_{n=0}^{N-1} x[n] \omega^ {0n}= \sum_{n=0}^{N-1} x[n]=x_0+x_1+x_2\dots+x_n$ $\quad X[1] = \sum_{n=0}^{N-1} x[n] \omega^ {1n}= \sum_{n=0}^{N-1} x[n]\omega^n=x_0+x_1\omega+x_2\omega^2\dots+x_n\omega^{N-1}$ $\quad X[2] = \sum_{n=0}^{N-1} x[n] \omega^ {2n}= \sum_{n=0}^{N-1} x[n](\omega^2)^n=x_0+x_1\omega^2+x_2\omega^4\dots+x_n(\omega^2)^{N-1}$ La Transformée de Fourier Discrète (DFT) d'un vecteur $\mathbf{x}$ de longueur $N$ peut être exprimée sous forme matricielle :  $$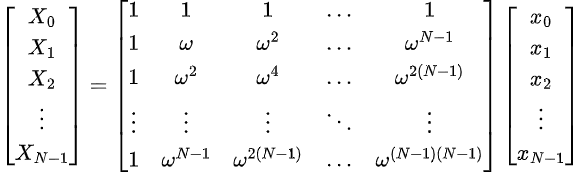X=W_n\times x$$ où : - $\mathbf{X}$ est le vecteur des coefficients de la DFT. - $\mathbf{x}$ est le vecteur des échantillons du signal. 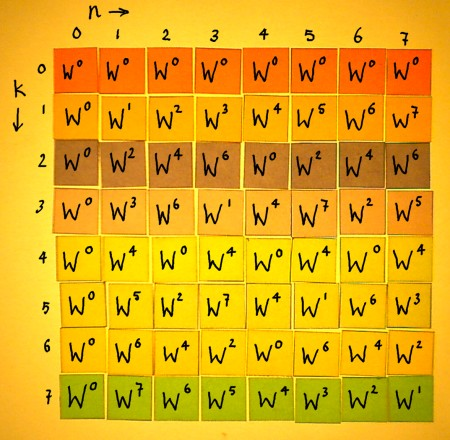- $W_n$ la matrice carrée (de Vandermonde) $W_2 = \begin{bmatrix} 1 & 1 \\ 1 & e^{-i \frac{2\pi}{2}} \\ \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & -1 \\ \end{bmatrix}$,$W_4=\begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & i & -1 & -i \\ 1 & -1 & 1 & -1 \\ 1 & -i & -1 & i \\ \end{bmatrix}$ :+1:Rq1: tous les termes $w^{kn}$ sont faciles à calculer Prenons l'exemple ci dessous N=8, $w=e^{-2\pi/8}$ k=3,les termes $w^{3n}=(w^3)^n$ sont faciles à calculer : on retrouve toutes les racines 8-ième de l'unité. :+1:Rq2: de plus $w^3$,$w-6$ sont conjugués, ainsi que leur puissance   --- - **TFD inverse :** $x=W_n^{-1}\times X$ , avec $W_n^{-1}$ facile à déterminer $$\quad x[k] = \sum_{n=0}^{N-1} X[n] e^{+j \frac{2\pi}{N} kn}$$ ==[en python](https://notebook.basthon.fr/?ipynb=eJzFWN1u2jAUfpXIVyE1lITw00g8ABebdtdKBKEMTBeROJnjqDDEZaVJk3iHrdseLE8yJ4SQDMcl_LTnKvb58Tnf-WxjVmCCHCcAxnAFXEStqUUtYKwAJWFA0RQY7AOtYWI1pksfAQNMvCkCEAReSCbxeEY8VwqWrr-UbNf3CJUUpkYLNAmp7eHxxAsxBYYKgRdSP6TxaqM1PH1B3O-Z-L7_DREvkDHENRM_9dHCl-sDRVN8-zaemXlEsiUbS8TCj0jGNcPEEpN4fs6Zj-V-aMP5qO97T_ITtJU5C_PQ_2BRYi_kodqAGmxBHbZhB3Zhb8S0vk9sTOWP8n2txqtZy9e8Sr93ZQWUIMtlbhQtmC2INj_VRlPiSMn0KwoTR5tffPWJkkRM1mw2us2u2ux0e6ra67T1nlQ_nIt-PEfP35lfnfnsBnWu6zVzPZB8Onwtbz5zumaufHTKgM3XwXd8U1xLoSvnaezxxnjelOOZJwbf8U3xFNK0FOy0iOtk-lKy-wWgFsrg98PE-zM4L5XplCn48U4XE4s4U5VnxX17-Vx5s2K2vHYWXj5H0V1RlWHF--Vd8TziDHx_LEV3dXG3Xj5XPtNeu3O5wa7Izsq7XQBp8VbhnXX86qPN72MLizZ_Dlgg2DGJeYXIh-mWdaVq5OO3-Zk5l-zLs_Mt7fuZ-QrO5aqRj6dqtPlrYvYgwZa7faBM2YsFrM96rO2fSMoD_5HUqvhI2pfX6hR6mmwY0a-eBA5mUNeZ34101-i0O722rul3-p3WyjfumChpo7ax9P_adXSU1F-9RC5ZPiIDUR71y-SRxjoVk5fUv6w_lyfpbEblBy45dRE5t9ZoTFAQOrTEPcuHEfjWdywbM89hTN28wAw0JfhKqKzVlEEyGuQ0A67VzV5TFnJrlLnAjLXF76LVCDDUcoiuz8OYBw8OHaf4t9CosCSYI4KRE_hoEo_SlvtL-sXDLRZwagcM0eU4VXxKFFKscSz8GFqPe3OwZvnhzzOPuNa2MbvB2LWxR4Chrf8B_BaAJg)== ,[fft interactive](https://ciiec.buap.mx/FFT.js/), [ou ici](https://engineering.icalculator.com/discrete-fourier-transform-calculator.html) :heart:[en python complet MPSI](https://notebook.basthon.fr/?from=https://raw.githubusercontent.com/matchre/Expert/refs/heads/master/2%20Complexes%20geometrique/fft.ipynb)[en pdf](https://www.mpsi-camille-guerin.fr/Python/FFT/FFT.pdf) #### Exemple 1 Pour n = 3, on considère $x_0 = 0, x_1 = 1$ et $x_2 = 2$(par exemple) La TFD de la séquence $(x_0, x_1, x_2)$ est la séquence $(X_0, X_1, X_2)$ avec : • $X[0] = \sum_{n=0}^{3-1} x[n] \omega^ {0n}= \sum_{n=0}^{2} x[n]=x_0+x_1+x_2= 0 + 1 + 2 = 3$ • $X[1] =\dots$ • $X[2] =\dots$  #### 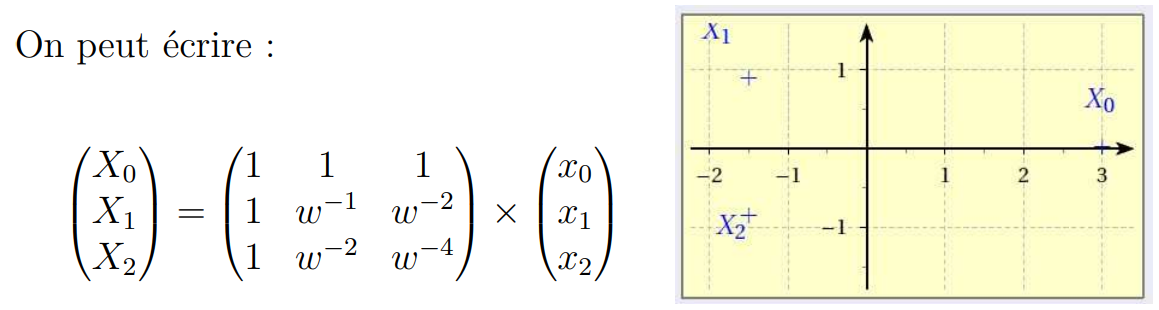Exemple 2:Signal rectangulaire, n = 8  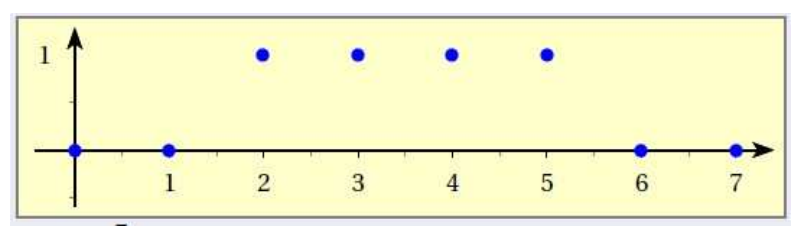1. Donner les valeurs des $x_k$ pour k compris entre 0 et 7. $\dots$ 2. Exprimer en fonction de w les valeurs de $X_p$ pour p compris entre 0 et 7 $\dots$ 3. Retrouver ce résultat sous forme de produit de matrice. X = F × x 4. 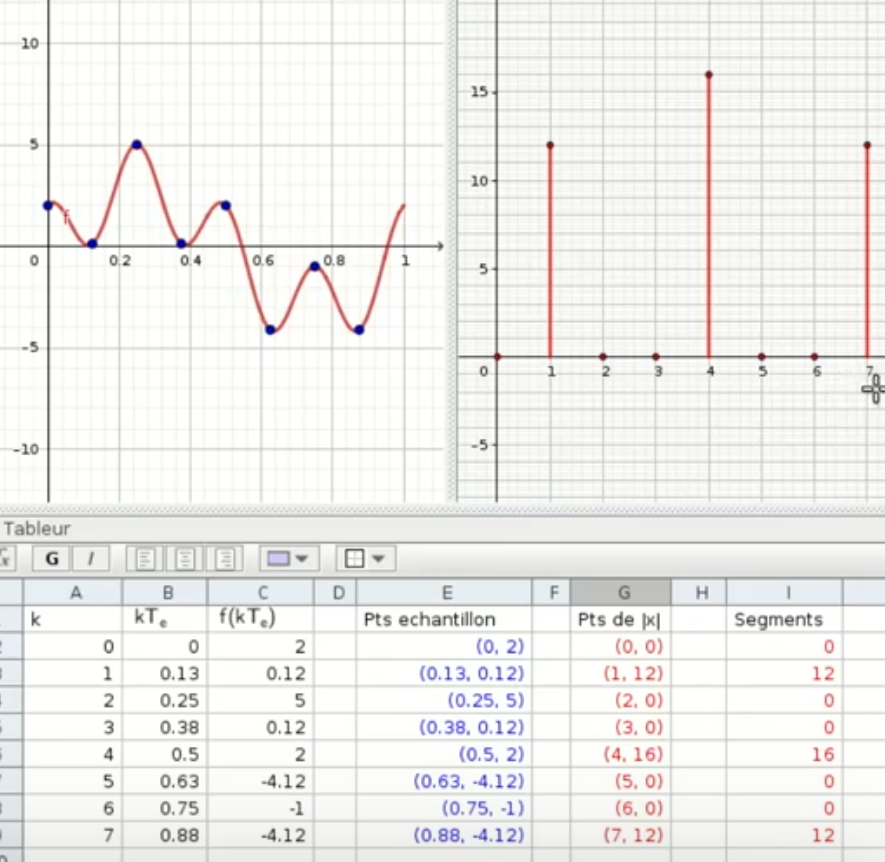Il est possible de représenter le diagramme de $(|X_0|, |X_1|, |X_2|, |X_3|, |X_4|, |X_5|, |X_6|, |X_7|)$  #### Exemple3: Soit le fonction $f(x)=3 sin(2 π x)+2 cos(8 π x)$. On la discrètise , les points x en haut à gauche puis on effectue la TFD et on représente $(|X_0|, |X_1|, |X_2|, |X_3|, |X_4|, |X_5|, |X_6|, |X_7|)$. On a $|X_1|=12 |X_4|=16$ ($|X_7|=4$ repliement de spectre ,qu'on associe à |X_4| ) On divise par 8, on retrouve 3 et 2  <iframe title="Transformée de Fourier discrète avec Geogebra : exemple d'utilisation et d'interprétation des résultats." width="560" height="315" src="https://tube-sciences-technologies.apps.education.fr/videos/embed/f6870f5c-4e9c-45ad-8baf-fc832aa038dc" frameborder="0" allowfullscreen="" sandbox="allow-same-origin allow-scripts allow-popups allow-forms"></iframe> --- ## IV.Transformée de Fourier Rapide (Cooley -Tukey) Il existe une façon de calculer la TFD beaucoup plus rapidement, c'est l'algorithme de Transformée de Fourier Rapide (sigle anglais : FFT ou fast Fourier transform). C’est celui utilisé par tous les logiciels de traitement du signal. En effet la multiplication de matrices demande $n^2$ multiplications.  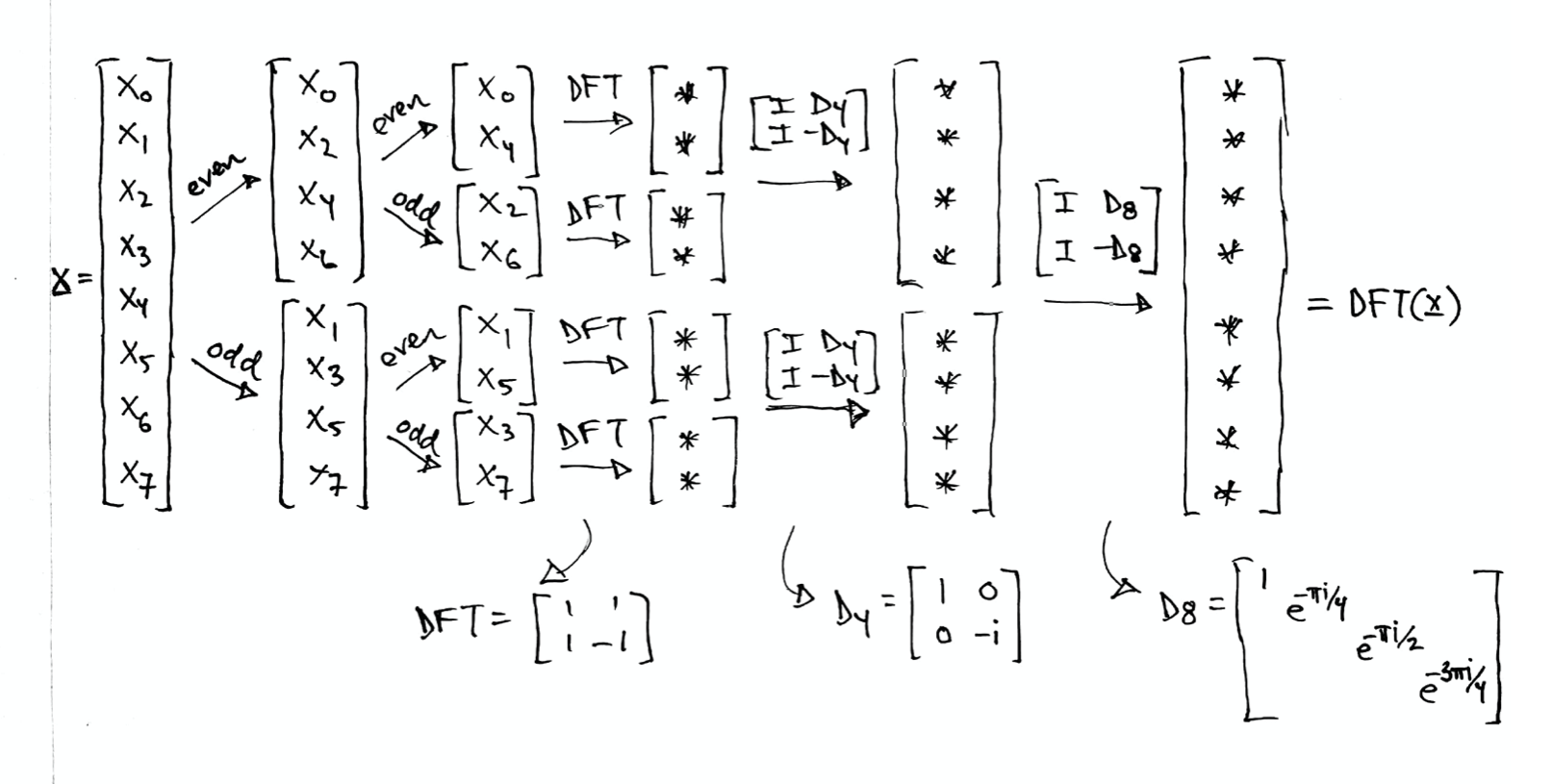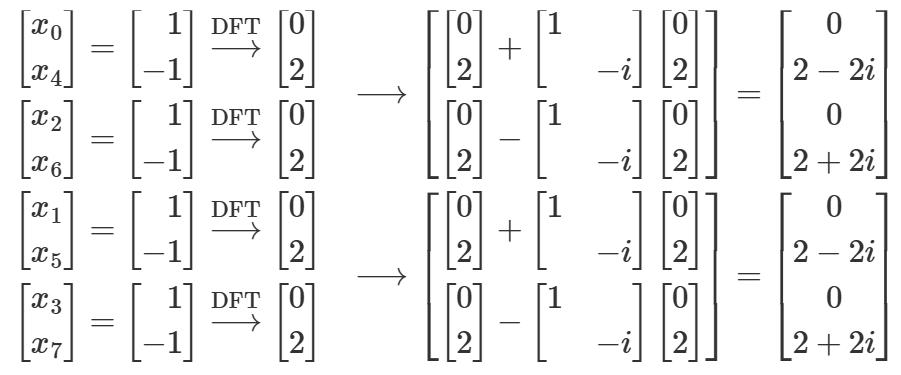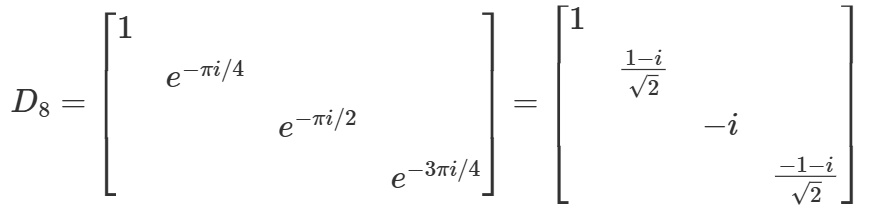**Il se base sur une approche de type ***« diviser pour régner »*** par le biais d'une récursion.**  $\begin{split} \boldsymbol{x} = \left[ \begin{array}{r} 1 \\ 1 \\ 1 \\ 1 \\ -1 \\ -1 \\ -1 \\ -1 \end{array} \right] \end{split}$  avec   :::spoiler exemple0 ## Exemple de la FFT pour un signal de taille 8 Considérons un signal simple $x = [1, 2, 3, 4, 5, 6, 7, 8]$. Voici comment on applique l'algorithme **FFT** à ce signal en suivant le principe de "diviser pour mieux régner". ### Étape 1 : Diviser le signal en deux groupes On commence par diviser le signal en deux groupes : - **Groupe pair** : $[1, 3, 5, 7]$ - **Groupe impair** : $[2, 4, 6, 8]$ ### Étape 2 : Diviser à nouveau en sous-groupes de taille 2 Ensuite, chaque groupe est divisé en deux sous-groupes : - **Groupe pair** : - $[1, 5]$ - $[3, 7]$ - **Groupe impair** : - $[2, 6]$ - $[4, 8]$ ### Étape 3 : Diviser encore jusqu'à obtenir des groupes de taille 1 On continue la division jusqu'à obtenir des sous-groupes de taille 1 : - **Groupe pair** : - $[1]$, $[5]$ - $[3]$, $[7]$ - **Groupe impair** : - $[2]$, $[6]$ - $[4]$, $[8]$ ### Étape 4 : Calculer la TFD sur les groupes de taille 1 La TFD de chaque sous-groupe de taille 1 est simplement la valeur elle-même : - **Groupe pair** : - $[1]$ - $[5]$ - $[3]$ - $[7]$ - **Groupe impair** : - $[2]$ - $[6]$ - $[4]$ - $[8]$ ### Étape 5 : Recombiner les résultats pour des groupes de taille 2 Ensuite, on recombine les résultats des groupes de taille 1 pour former des groupes de taille 2 : #### 1. Combiner les groupes du groupe pair : - [1] et [5]: $X_0 = 1 + 5 = 6$ $X_1 = 1 - 5 = -4$ - $[3]$et $[7]$: $X_0 = 3 + 7 = 10$ $X_1 = 3 - 7 = -4$ #### 2. Combiner les groupes du groupe impair : - $[2]$et $[6]$: $X_0 = 2 + 6 = 8$ $X_1 = 2 - 6 = -4$ - $[4]$et $[8]$: $X_0 = 4 + 8 = 12$ $X_1 = 4 - 8 = -4$ ### Étape 6 : Combiner les résultats pour des groupes de taille 4 On recombine ensuite les résultats des groupes de taille 2 pour former des groupes de taille 4 : - **Groupe pair** : - $[6, -4]$et $[10, -4]$ - $X_0 = 6 + 10 = 16$ - $X_1 = -4 + (-4) = -8$ - $X_2 = 6 - 10 = -4$ - $X_3 = -4 - (-4) = 0$ - **Groupe impair** : - $[8, -4]$et $[12, -4]$ - $X_0 = 8 + 12 = 20$ - $X_1 = -4 + (-4) = -8$ - $X_2 = 8 - 12 = -4$ - $X_3 = -4 - (-4) = 0$ ### Étape 7 : Combiner les résultats finaux pour obtenir la TFD complète Enfin, on combine les résultats des deux groupes de taille 4 pour obtenir la TFD complète : - $[16, -8, -4, 0]$et $[20, -8, -4, 0]$ - $X_0 = 16 + 20 = 36$ - $X_1 = -8 + (-8) = -16$ - $X_2 = -4 + (-4) = -8$ - $X_3 = 0 + 0 = 0$ - $X_4 = 16 - 20 = -4$ - $X_5 = -8 - (-8) = 0$ - $X_6 = -4 - (-4) = 0$ - $X_7 = 0 - 0 = 0$ ### Résultat final : La TFD complète du signal $x = [1, 2, 3, 4, 5, 6, 7, 8]$est donc : $[36, -16, -8, 0, -4, 0, 0, 0]$ ## Conclusion Grâce à l'approche "diviser pour mieux régner", on divise le problème en sous-parties plus petites, et on combine les résultats à chaque étape. Cela permet de calculer la TFD de manière plus rapide que la méthode classique. 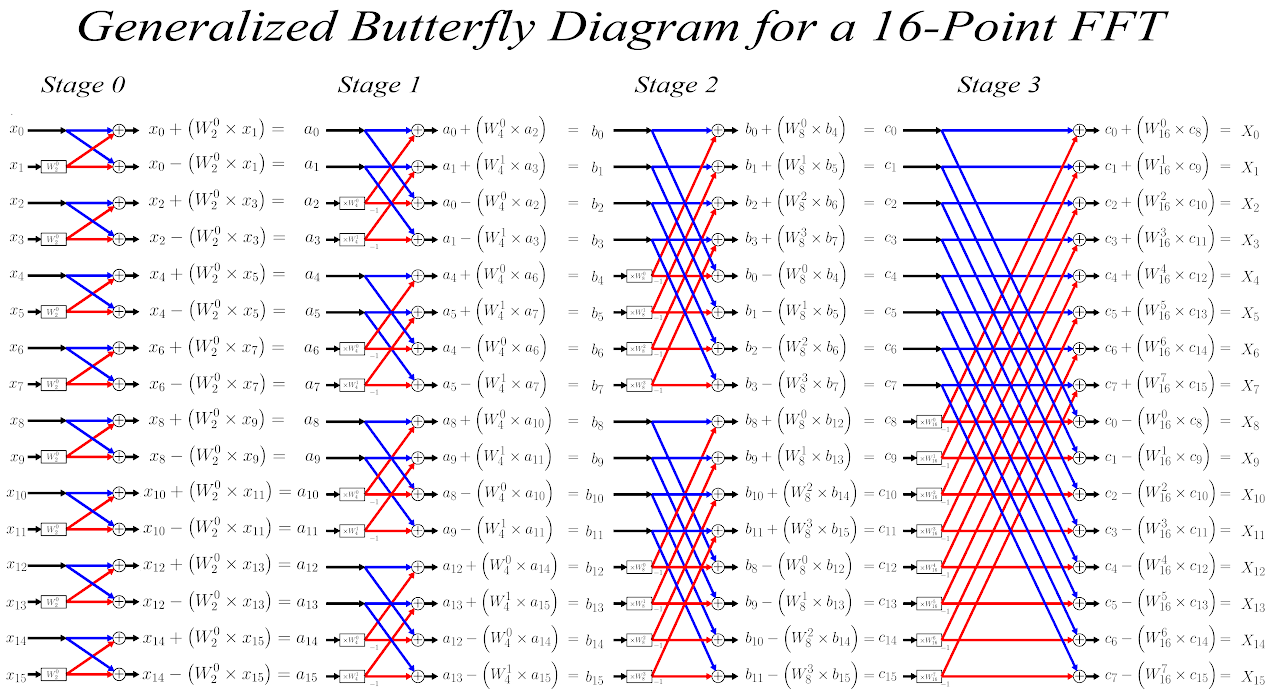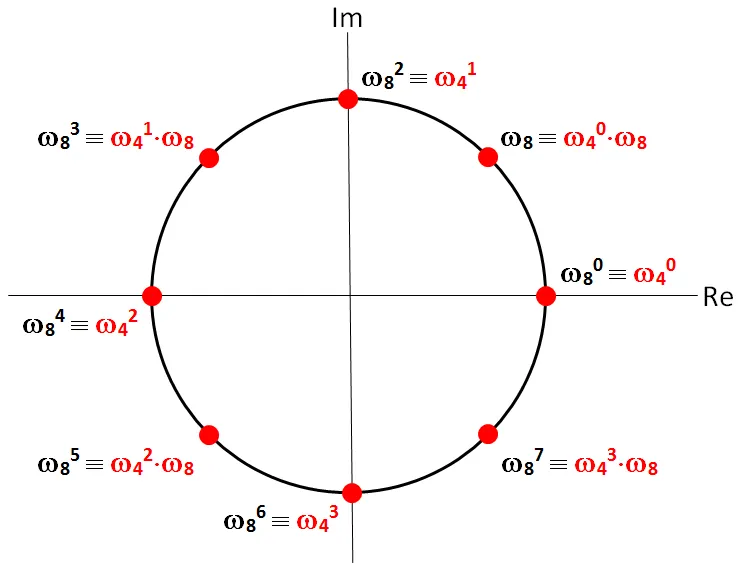::: **Exemple 1: n=4**   **Exemple 2: n=16** Ici au lieu d'avoir $16\times 16$ multiplications, on n'en a besoin que de 64  Avec $\omega_8$ la racine 8-ième de l'unité telle que $\omega_8^8=1$ et $\omega_4$ la racine 4-ième de l'unité telle que $\omega_4^4=1$ L'idée étant que de se ramener à une puissance de 2 inférieure , permet moins de calculs Et on répète ce procédé  ## V.Applications ### 1.Polynômes et FFT LA TFD transforme la convolution en simple produit. https://capytale2.ac-paris.fr/web/c/844d-5541312 [lien sans authentification](https://notebook.basthon.fr/?ipynb=eJytV-tu2zYUfhVWCTBfZFmirjbqAUnbAAE6LCjyL04MWqITphKliZTrrMi77N_WvcGwn36xHVK-212atAkS3g7P-c7huemzEdM0FUb_6rORUUkSIonR__xo6v2RfCio0TcyUn5M8k_cMA2RV2Ws9o7QL1UqWZGymEiWc5RQdFsSnghEuWS0FGjIj44QmdIYpQRdwpmY5GU2_0KFIj4DTkCG3jIRl_O_JEUNRKUiPTu7bBqP5nMRXb2hMUMTwiQqSAkQUPJTxSkqyvkXAZhqmPM_NJqztwATZUTeAd5ZQUt53biTshD9bjfOE5YlFikKYdGkqvWzJmVXdMuL2_vLC5mcvgQgWONXjqa0kihb2A70b7Uc7HoKMvKDMGq1hnzIXydsiuKUCDEYGiQFeEj_7zA-yYfGz0P-JueCJfMvJYzoWLEYOEM5HEqWgX0Rcuwbt413dnDb3dlx2t7Ojj04aTh28xier347sGCePvA8o-j45BhJmqLfKjVvzJpKJlyb1bL0TMvQM81bz-xjS2n1TqJ4C7ZSeODvwQ72YId7sKM92Kca9iHUpxuoTxVqf4U6WKEOV6ijFWoF-g1J4wpsj7aeCZV0ysCplD_FSwoltMyTCjzwRFOeao-ma4oCfAHNBo6tOSt_pUIZZf6vpNVMu-RWVAkTnDif_6N8FiJH3uUQOaJiU8Il7b_ugpuAL7zIF4_QuYVq5VQ8iq9HaLKKUBU2cHCi1ILx9GlHvVAKAxiCIPaAKo8hLgmounwdgU5MsFNKK8gYcU4nExYrwwrUqMkheJUsu7YdKUs2BUxgdh3bFROC8JgqEmzCVRRtcWkqQ0PU5WOpn6vVguwyOmm1lAr14hQWtSV37WjIshKSJkZ_QlJBd8wKaYJumpRlRQ7q8yorHkBVxIsh18IGvLAmE6n-Glee6ZrYdEy7_r1u1kSnW0SRGZqB6W8SFSXjsqH5ba0gE5kGndG4Uv4yivOKS6Pv-KaRV7KoZJ3b6_kSuZAlJRnck3QmVeZ0bAstftq2dY9WP77lOR52XD_oeFaEIw-HDoZzvKLvYOt-yNWOH_lhFHhexz5Muc15Td_eoK85rW7gw1jaG1iuh_wKB6srO1J6a_yOZ3mRjyPHDXfEaB3Wd4IVMnXwtTvbcjbutP_nDj6Mrb2JDRSCl-Ekq18qgaczHq9fGOEQ4pfAAKKjzlZFWgkkwFMhKSUQ7io5ZTlP6Ea8Px3U7ziCCFOpDcJwmZ12uwGxGeJIQoxDAE9VdZ7_Df4HhVpIljBaCWpCFhTkgf6OXqlwfX-Q2zemJxPpGFHhrcNDJ1gJSYOBCgj1d1lLWkKJAD30RFepGVX26UNVmeFggAP7R2QHjWo0yZkY1fEeta5seGvQCDHEOAL1bmkjavaV0yC0S3_Frgd6Dyat5c4yEexRH04K3rOSQgM0b9v3TRM1Ok5k9ULbD3DoRV4YOi7EE3atKMLYt3s9t2eD-yvSTnQP9ODP2-Rhx3G2qQNfc_YWEvZvtA_f0PwP4GkfwvNjY-nc-kClKkJ7kQMNjWo5Dza7m656zqF2Cfr9nrRgNNrzqkUVYaqM7DnFZt34GofDnuM8y3NcbOn06C_GwFmMdj26Xj06QT1Caq_H-vxHvdpTaew93ek4CpUCpFSJErquMUxYWfe5y1az7h5nN-BuwezGb7ve7MZrB7ZuJR3VRvpYtZAuXraPQ_4BMhD0PGkODc5mt6ib9iVj3VMOkG6918JgMfDVfy1QT5RMPVFi9URJ1hMlXE-UfD1ZQtiXNQhtOwh8fHw4t31jTEAhUB9XFfj501Vjs4WFgIlLBmYB05v6m43qJJ_RckpZmurqoSINJouvSqgk4xKWjfxjfaaJqGRyfTaF6qZ6wPmfRPXfqtgwDp6c0uayVx7yV1frT72McZYf-NKrPwE7qpvvVkWak0QsxpGbOK5jj4MxppPA8z07iDHteZPE6dHQx45V8Nvmi3ry7wSGAw97PeKHCaaUeNSLo9Cf2C723WhCJqEG9p2walHWJ_YRPClhxMrL265aFWoF6DLIiaIr76ps3A26Qa97Dh8qt7QcbZfd0fhBpRtLTG-7IfaLWedJuoPwn5c5D6U2XqXpZnK7frw2tyR8pCWnqShorFaLrFQ8gB9zFxhC91Gk5GG0OLjQB0idpFDQK3K7JjceAR8fq7pAQLK3XozgufPS6OPH_wCju5oa)  {%youtube wAfE1aXbq1I %} {%youtube h7apO7q16V0 %} ref: https://perso.crans.org/moubeche/SNIR2/5_TFD/Thomas/26C1%20Transformee%20de%20Fourier.pdf ### 2.(épi)ⁿ-cycloïdes :::warning **Soleil,Terre,Lune** elles tourne, tournent, tournent... 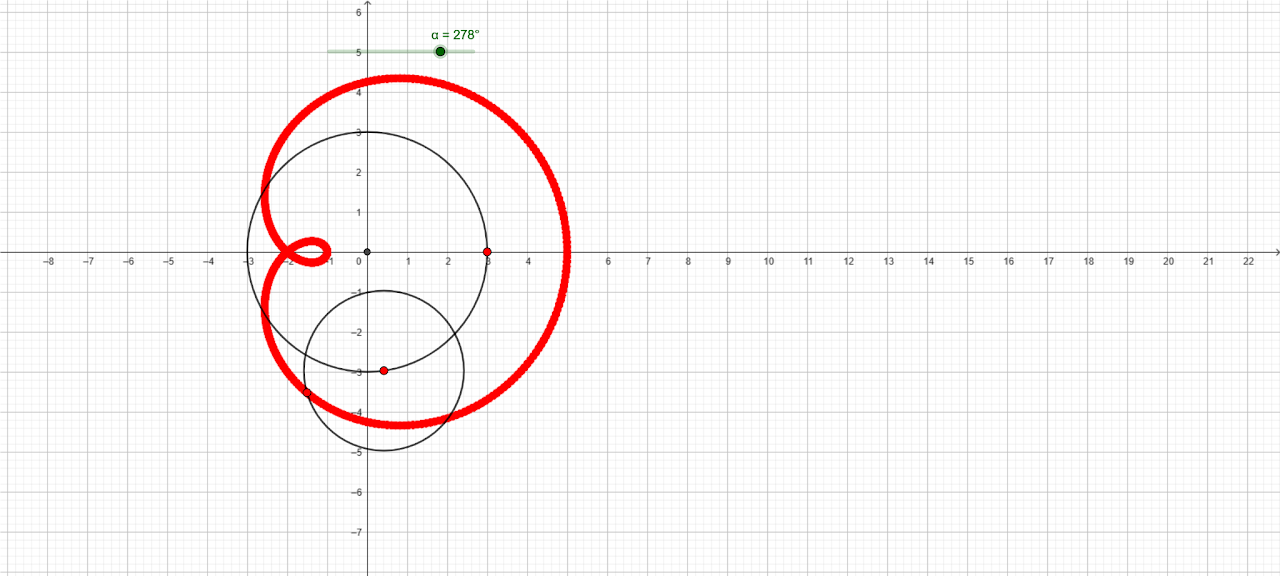::: Et si la lune était 50 fois plus éloignée de la terre… [anim](https://math.univ-lyon1.fr/~alachal/diaporamas/diaporama_cycloides/images_cycloides/orbite_lune04b.gif) :::warning Avec Geogebra $$3 ℯ^{i α}+2 ℯ^{i 2α}$$ ::: [anim](https://www.geogebra.org/classic/er8kqwpj) Une excellente question à se poser, c'est celle de l'équation des courbes que l'on obtient.  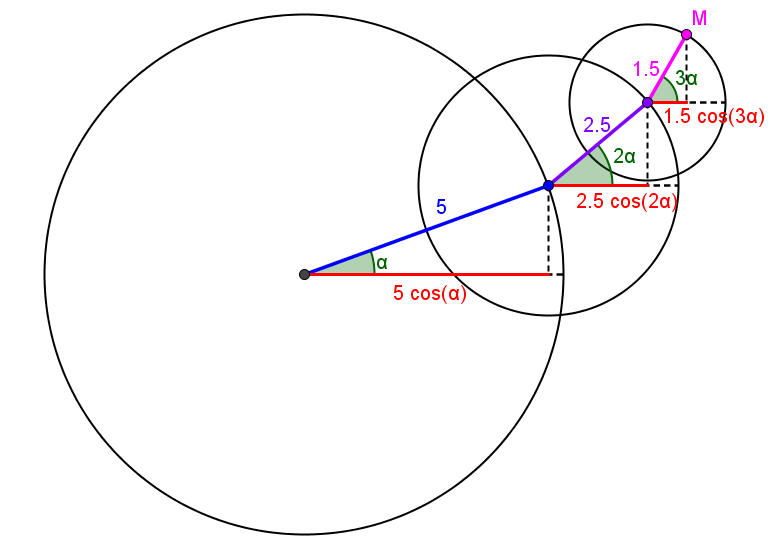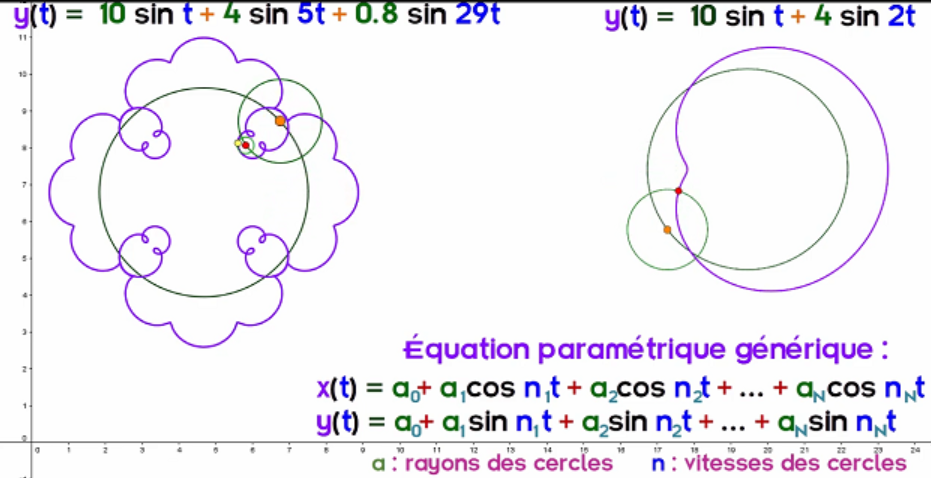Le point M a pour affixe: $$z=5e^{i\alpha}+2,5e^{i3\alpha}+1,5e^{i3\alpha}$$ [anim geogebra](https://www.geogebra.org/m/kfgqpxac#material/kwtkaqg7) , [anim2](https://www.geogebra.org/m/kfgqpxac#material/gcdmcxhu) , [anim3](https://www.geogebra.org/m/kfgqpxac#material/xptbvmkw) {%youtube uazPP0ny3XQ %}  :::warning Dessiner un éléphant avec des cercles ! 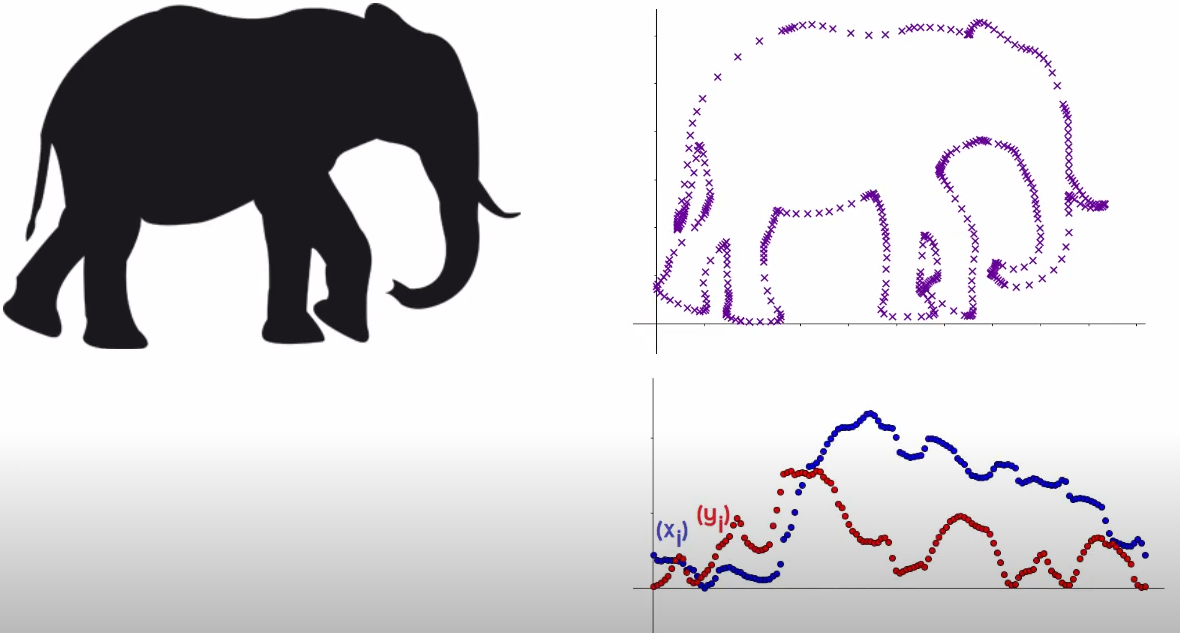:::  Figure à main levée (continue, périodique,pas d'équation math) On discrètise pour avoir un nombre fini de points $(x_n,y_n)$ avec $n=0...N-1$ On calcule les TFD X et Y: - $$\quad X[k] = \sum_{n=0}^{N-1} x[n] e^{-j \frac{2\pi}{N} kn}$$ - $$\quad Y[k] = \sum_{n=0}^{N-1} y[n] e^{-j \frac{2\pi}{N} kn}$$ Puis la TFD inverse permet d'avoir : - $$\quad x[k] = \sum_{n=0}^{N-1} X[n] e^{+j \frac{2\pi}{N} kn}$$ - $$\quad y[k] = \sum_{n=0}^{N-1} Y[n] e^{+j \frac{2\pi}{N} kn}$$  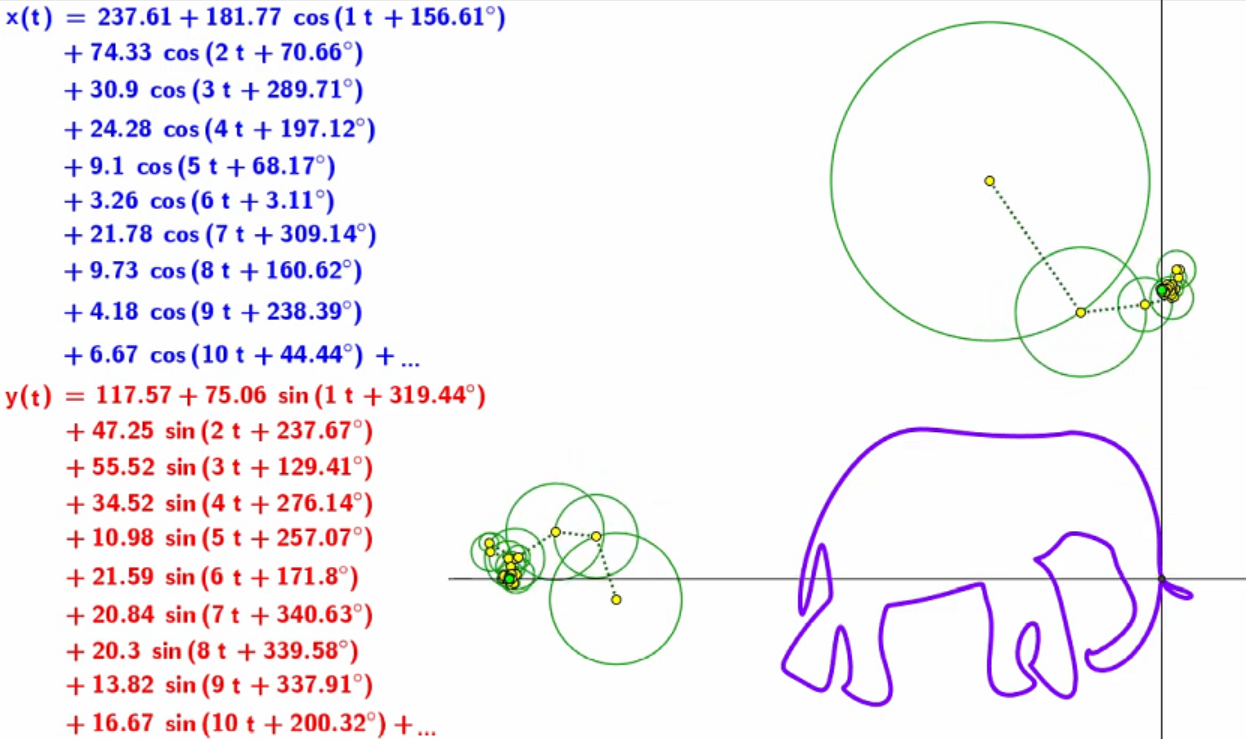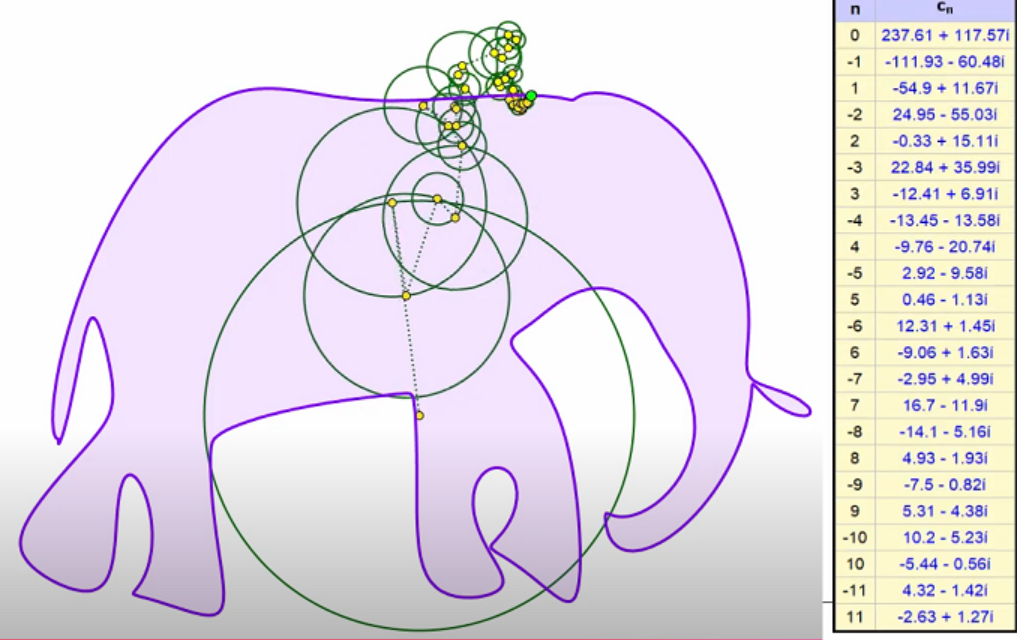Rq: si on considère les points $(x_n,y_n)$ comme des nombres complexes $y_n=x_n+iy_n$,on peut alors calculer Z, la TDF de x: $$\quad Z[k] = \sum_{n=0}^{N-1} z[n] e^{-j \frac{2\pi}{N} kn}$$ Puis la TFD inverse permet d'avoir : - $$\quad z[k] = \sum_{n=0}^{N-1} Z[n] e^{+j \frac{2\pi}{N} kn}$$  https://www.dynamicmath.xyz/fourier-epicycles/ https://ubcmath.github.io/MATH307/dft/convolution.html https://www.mpsi-camille-guerin.fr/Python/FFT/FFT.pdf https://notebook.basthon.fr/?from=https://raw.githubusercontent.com/matchre/Expert/refs/heads/master/2%20Complexes%20geometrique/fft.ipynb <style> h1{text-align: center;color: white; background-image: linear-gradient(to right , #ffca08, #DBAF0D) ;border-radius: 10px;} h2{ color:#0070C0} </style>