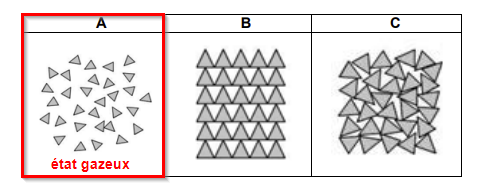
--- title: Correction de l'épreuve du Brevet Série Générale Centres Étrangers du Groupe 1 (2025) tags: correction, DNB, 2025 --- ## ++Partie 1++ : Fabrication de l'ammoniac (14 points) ### 1. Modélisation de l'ammoniac dans les <abbr title="Conditions Normales de Température et de Pression">CNTP</abbr> **Dans le document 1, la modélisation A représente l'ammoniac, qui est un gaz dans les conditions normales de température et de pression**.  :::spoiler **<span style="background-color: #D0F0C0; border-radius: 10px; padding: 5px;">Explication du choix</span>** <span style="color: blue;">*À l'état gazeux, les molécules sont ++espacées et équitablement réparties++ dans tout le volume du contenant. Elles sont également ++totalement libres++, et ++se déplacent très rapidement++ (ce qui ne peut être représenté sur un schéma).*</span> ::: ### 2. Composition de la molécule d'ammoniac **La molécule d'ammoniac a pour formule chimique $NH_3$, elle est donc composées de :** * **1 atome d'<span style="color: blue;">azote</span>** $(\color{blue}{N}H_3)$ * **3 atomes d'<span style="color: grey;">hydrogène</span>** $(N\color{grey}{H_3})$ ### 3. Type de transformation et justification Soit l'équation de réaction $N_2 + 3\,H_2 \rightarrow 2\,NH_3$. **La synthèse de l'ammoniac est une transformation chimique car la composition chimique des substances change : ++les atomes des molécules de réactifs++ (diazote et dihydrogène) ++se combinent pour créer une nouvelle molécule de produit++ (l'ammoniac)**. ### 4. Proportion de diazote **Dans l'air atmosphérique, il y a 80% en volume de diazote**. :::spoiler **<span style="background-color: #D0F0C0; border-radius: 10px; padding: 5px;">Connaissance à avoir pour répondre correctement</span>** <span style="color: blue;">*L'air atmosphérique est un mélange de nombreux gaz, ++les deux principaux sont le diazote (environ 80% en volume) et le dioxygène (environ 20% en volume)++.*</span> ::: ### 5. Masse de dihydrogène nécessaire **On rappelle qu'au cours d'une transformation chimique, il y a conservation de la masse totale : la masse totale des réactifs consommés doit être égale à la masse totale des produits fabriqués (Loi de Conservation de la Masse)**. Si on note $m(N_2)$ la masse de diazote nécessaire, $m(H_2)$ celle de dihydrogène nécessaire et finalement $m(NH_3)$ la masse d'ammoniac formé, alors on peut écrire : $m(N_2)+m(H_2)=m(NH_3)$ avec $\left\{\begin{array}{ll}m(NH_3)&=1\text{ t}=1\,000\text{ kg}\\m(N_2)&=824\text{ kg}\end{array}\right.$ Soit : $824\text{ kg}+m(H_2)=1\,000\text{ kg}$ $m(H_2)=1\,000\text{ kg}-824\text{ kg}$ $m(H_2)=176\text{ kg}$ **Pour former 1 tonne d'ammoniac, il faudra 176 kilogrammes de dihydrogène**. ## ++Partie 2++ : Épandage d'un engrais (11 points) ### 6. 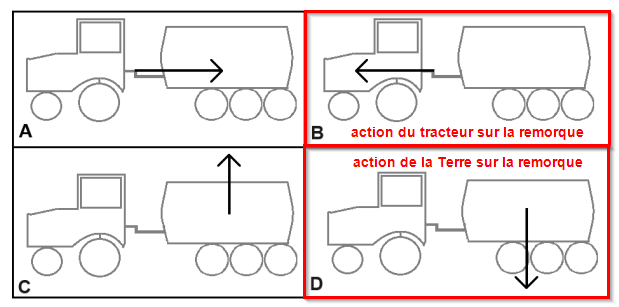Choix des modélisations des actions mécaniques remorque-épandeur * **L'action mécanique exercée par le tracteur sur la remorque (action 1) est modélisée par le schéma B** ; * **L'action mécanique exercée par la Terre sur la remorque (action 2) est modélisée par le schéma D** ;  :::spoiler **<span style="background-color: #D0F0C0; border-radius: 10px; padding: 5px;">Connaissances à avoir pour répondre correctement</span>** <div style="color: blue;"><ul> <li><i>L'<b>action du tracteur sur la remorque</b> est une <u>action de contact localisée</u> dont l'effet est de tirer la remorque vers l'avant : ce doit doit être un segment fléché <u>horizontal</u> ayant pour <u>origine le lieu de contact tracteur/remorque</u> dans le <u>sens de déplacement du tracteur</u>.</i></li> <li><i>L'<b>action de la Terre sur la remorque</b> est une <u>action à distance répartie</u> dont l'effet est d'attirer la remorque vers le centre de la Terre : ce doit doit être un segment fléché <u>vertical</u> ayant pour <u>origine le centre de gravité de la remorque</u> orienté <u>vers le bas</u>.</i></li> </ul> </i></div> ::: ### 7. 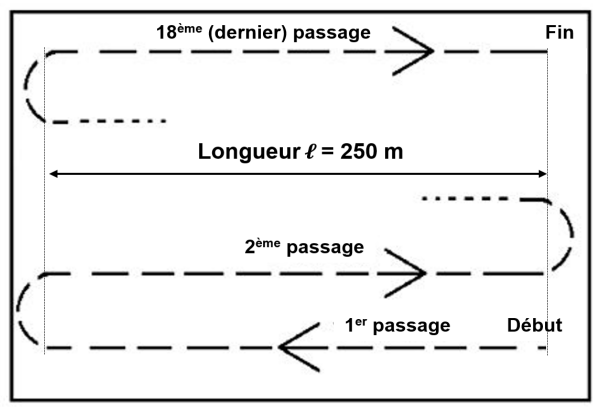Durée d'épandage sur un champ  Si l'on ne tient pas compte des manoeuvres en bout de champs, pour parcourir la totalité du champ, le tracteur devra faire 18 passages, soit parcourir une distance : $d=18\times l$ , avec $l=250\text{ m}=0,250\text{ km}$ La relation entre $d$, $v$ et $t$ peut s'écrire : $t=\dfrac{d}{v}$ Avec $\left\{\begin{array}{ll}d&=18\times l= 18\times0,250\text{ km}\\v&=9\text{ km/h}\end{array}\right.$ , soit $t=\dfrac{18\times 0,250\text{ km}}{9\text{ km/h}}=2\times0,250\text{ h}=0,5\text{ h}$ **Il faudra 0,5 heure (soit 30 minutes) pour répandre l'angrais sur la totalité du champ**. :::spoiler <span style="background-color: #D0F0C0; border-radius: 10px; padding: 5px;">**Retrouver la bonne relation pour la calcul**</span> <div style="color: blue;"><i> <br/>On connaît par coeur la relation $v=\dfrac{d}{t}$ Cela peut aussi s'écrire : $\dfrac{v}{1}=\dfrac{d}{t}$ <u>Produit en croix</u> : $\dfrac{v}{1}=\dfrac{d}{t} \Leftrightarrow v\times t = d\times 1$ Or $v\times t = d$ peut aussi s'écrire $\dfrac{\not{v}\times t}{\color{red}{\not{v}}}=\dfrac{d}{\color{red}{v}}$ et donc finalement $t=\dfrac{d}{v}$ </i></div> ::: ### 8. Forfait de location à choisir  Pour traiter 10 champs identiques, à raison d'un temps moyen de traitement d'un champs de $t_\text{moy}=45\text{ min}$, il faudra un temps total $t_\text{tot}$ : $t_\text{tot}=10\times t_\text{moy}=10\times 45 = 450\text{ min}$ À convertir en heure : $t_\text{tot} = 450\text{ min} = \dfrac{450\text{ min}}{60\text{ min/h}}=7,5\text{ h}$ **Il faut donc choisir le forfait B avec une durée de location de 8 heures ($8\text{ h}>7,5\text{ h}$)**.