--- title: "SOLUTION ALTERNATIVE pour le groupe Transat / modélisation 3D en vue de son impression 3D" author: Carole le Beller lang: fr date: Janvier 26, 2025 tags: Carole Le Beller, cône de révolution, demi-cône de révolution, calculs mathématiques, MPLS Bretagne, Maison Pour La Science Bretagne, Commission Inter IREM TICE, C2i TICE, IREM de Rennes --- --- --- # <center>SOLUTION ALTERNATIVE </center> # <center> <i class="fa fa-gear fa-spin" style="color: firebrick"></i> </center> # <center>Pour le groupe "*Transat*",</center> # <center>Stage DESIGN 2025 de la MPLS Bretagne</center> --- ## <center> Modélisation 3D en vue de son impression 3D </center> ## <center> avec GeoGebra 3D </center> </br> <center> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_715e9b1ad3a8571ee72fd9a2ab05d502.gif" alt="Secteur circulaire avec l'angle de 60° encore plus éloigné sector_diagram_60_degree_farther.svg, converti en png" width="50%"></center> </br> ## *<center>------ - ------</center>* #### *<center>Par Carole LE BELLER</center>* <center> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_5282cb7b0ace4fce03a8d6797c1a7bb9.png" alt="logo Carole LE BELLER" width="10%"></center> --- --- ## Plan 2D réalisés avec GeoGebra 2D et les outils languettes ### À disposition - Plan 2D manuscrit et une photographie *(voir dans la colonne "2025-Productions des stagiaires" puis "2025 - Le transat pour bonhomme "boule à thé"" : https://digipad.app/p/933763/6398815864bb)* du groupe 'Transat' *(composé de Christelle LE BRUSQ-PREMEL, Mathilde MANINI et Christophe MENARD, stage Design 2025 MPLS Bretagne.)* - Mémoire visuelle de la réalisation en papier cartonné par le groupe "Transat" - Plan 2D refait dans GeoGebra 2D et les outils languettes (outils créés par Carole LE BELLER pour GeoGebra) utilisés pour réaliser un patron sans colle à destination d'une découpeuse à lame (Silhouette Portrait) : <center> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_dd6f55b298ffab0bcda8e1db13f4577a.png" alt="Plan 2D refait dans GeoGebra 2D, converti en png" width="50%"><img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_d59d91b39503464564b2ea370def62fb.png"alt="patron réalisé avec GeoGebra 2D, converti en png" width="50%"> </center> <center><em>Réal. Figures par Carole LE BELLER</em></center> </br> Fichier : https://www.geogebra.org/m/qtq3raq4 --- --- # Étape 1️⃣ : Calculs mathématiques pour la construction du cône de révolution connaissant son patron :::info ### Données initiales Un cercle de rayon $R = 5\,\text{cm}$ est découpé en un secteur circulaire correspondant à un angle au centre de $60^\circ$. La longueur du grand arc $L$ est associée au complément de ce secteur. Ce dernier est utilisé pour construire un cône de révolution. </br> ::: ### Croquis correspondants aux données 1. Un cercle de rayon $R = 5\,\text{cm}$ avec une portion de $60^\circ$ marquée. La longueur de la base du cône de révolution à construire est $L$. <center><img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_e396a66fc759d6d12072c80a36259aff.png" alt="Secteur circulaire avec l'angle de 60° encore plus éloigné sector_diagram_60_degree_farther.svg, converti en png" width="35%"> </center> :sparkles: *Figure réalisée avec l'assistance de l'IA ChatGPT 4o mini* 2. La hauteur $h$ est perpendiculaire à la base $[AB]$. Le triangle $ABH$ est donc rectangle en $A$, où $H$ est le sommet du cône, $AB = r$ est le rayon de la base circulaire, et $AH = h$, $BH = R = 5\,\text{cm}$. <center><img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_78f6729eb909c3053ffab454a6144fa7.png " alt="Triangle rectangle ABH triangle_AHB_corrected.svg, converti en png" width="40%"></center> --- ## a) Calcul de $r$, le rayon de la base du cône de révolution Le rayon $r$ est le rayon de la base du cône à construire. La longueur $L$ correspond à l'arc de cercle du secteur circulaire et est donnée par : $$ L = \frac{360^\circ - 60^\circ}{360^\circ} \times 2 \pi R $$ Substituons les valeurs : $$ L = \frac{300^\circ}{360^\circ} \times 2 \pi \times 5 $$ $$ L = \frac{25 \pi}{3}\,\text{cm} $$ Sachant que $L = 2 \pi r$, où $r$ est le rayon de la base du cône, nous avons : $$ r = \frac{L}{2 \pi} = \frac{\frac{25 \pi}{3}}{2 \pi} $$ $$ r = \frac{25}{6}\,\text{cm} $$ :::success >**Valeur exacte :** $r = \frac{25}{6}\,\text{cm}$. **Pour indication :** $r \approx 4,17\,\text{cm}$. ::: --- ## b) Calcul de $h$, la hauteur du cône de révolution Dans le triangle rectangle $ABH$, rectangle en $A$, on utilise le théorème de Pythagore. La relation est : $$ HB^2 = AH^2 + AB^2 $$ $$ HB^2 = h^2 + AB^2 $$ Sachant que $HB = R = 5\,\text{cm}$ et $AB = r = \frac{25}{6}\,\text{cm}$, nous avons : $$ 5^2 = h^2 + \left(\frac{25}{6}\right)^2 $$ $$ h^2 = 25 - \left(\frac{25}{6}\right)^2 $$ Calculons : $$ h^2 = 25 - \frac{625}{36} $$ $$ h^2 = \frac{900}{36} - \frac{625}{36} $$ $$ h^2 = \frac{275}{36} $$ $$ h = \sqrt{\frac{275}{36}} = \frac{5 \sqrt{11}}{6}\,\text{cm} $$ :::success >**Valeur exacte :** $h = \frac{5 \sqrt{11}}{6}\,\text{cm}$. > **Pour indication :** $h \approx 2,8\,\text{cm}$. ::: --- :::danger ### Résumé des résultats - Rayon de la base du cône : $r = \frac{25}{6}\,\text{cm}$ ($\approx 4,17\,\text{cm}$). - Hauteur du cône : $h = \frac{5 \sqrt{11}}{6}\,\text{cm}$ ($\approx 2,8\,\text{cm}$). </br> ::: <center><img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_7b4fd7fc1a0876a58477dc70af2c1b36.png " alt="cône de révolution effectué dans GeoGebra et converti en png" width="40%"></center> --- --- # Étape 2️⃣ : Construction du demi-cône dans GeoGebra 3D ## Éléments de code à saisir successivement dans GeoGebra 3D A = (0, 0, 0) // Centre de la base H = (0, 0, (5 * sqrt(11)) / 6) // Sommet du cône r = 5 // Rayon de la base h = (5 * sqrt(11)) / 6 // Hauteur du cône // Demi-cercle représentant la base (dans le plan XOY) B = (r, 0, 0) // Point à l'extrémité droite C = (-r, 0, 0) // Point à l'extrémité gauche c: ArcCercle(A,B,C,PlanxOy) // Demi-cercle // Génératrices reliant les extrémités de la base au sommet Segment[H, B] // Génératrice droite Segment[H, C] // Génératrice gauche // Surface paramétrique pour le demi-cône demicone=Surface((r cos(t) (1-s),r sin(t) (1-s),h s),t,0,π,s,0,1) :sparkles: *Code GeoGebra écrit avec l'assistance de l'IA ChatGPT 4o mini* ## Explication des éléments du code **1. Points A et C** - $A = (0, 0, 0)$ : Ce point représente le centre de la base du cône, situé à l'origine du plan XY. - $H = \left( 0, 0, \frac{5 \sqrt{11}}{6} \right)$ : Le sommet du cône est situé à une hauteur spécifique dans l'axe Z, avec la valeur $h$ qui est déterminée par cette expression. **2. Points P1 et P2** - $B = (r, 0, 0)$ et $C = (-r, 0, 0)$ : Ces deux points sont les extrémités de la base circulaire du cône, de part et d'autre de l'axe X, à une distance $r$ du centre $A$. **3. Base circulaire** - $\text{Base} = \text{Arc}(A, B, C)$ : Ce code crée un arc de cercle représentant la demi-base du cône. L'arc va de $B$ à $C$ de centre $A$. **4. Génératrices** - $\text{Segment}[HB]$ et $\text{Segment}[HC]$ : Ces segments relient le sommet du cône $H$ aux points extrêmes $B$ et $C$ de la base, formant les côtés du cône. **5. Surface paramétrique** La surface est définie par une fonction paramétrique où $t$ et $s$ sont des paramètres : - $t$ représente l'angle de rotation autour de l'axe $Z$ (allant de $0$ à $\pi$ pour former un demi-cercle), - $s$ contrôle l'altitude de la surface (allant de $0$ à $1$, où $0$ est à la base et $1$ est au sommet). Cela produit un demi-cône avec un rayon de base de $r$ et une hauteur de $h$, dont la surface est générée de manière paramétrique. 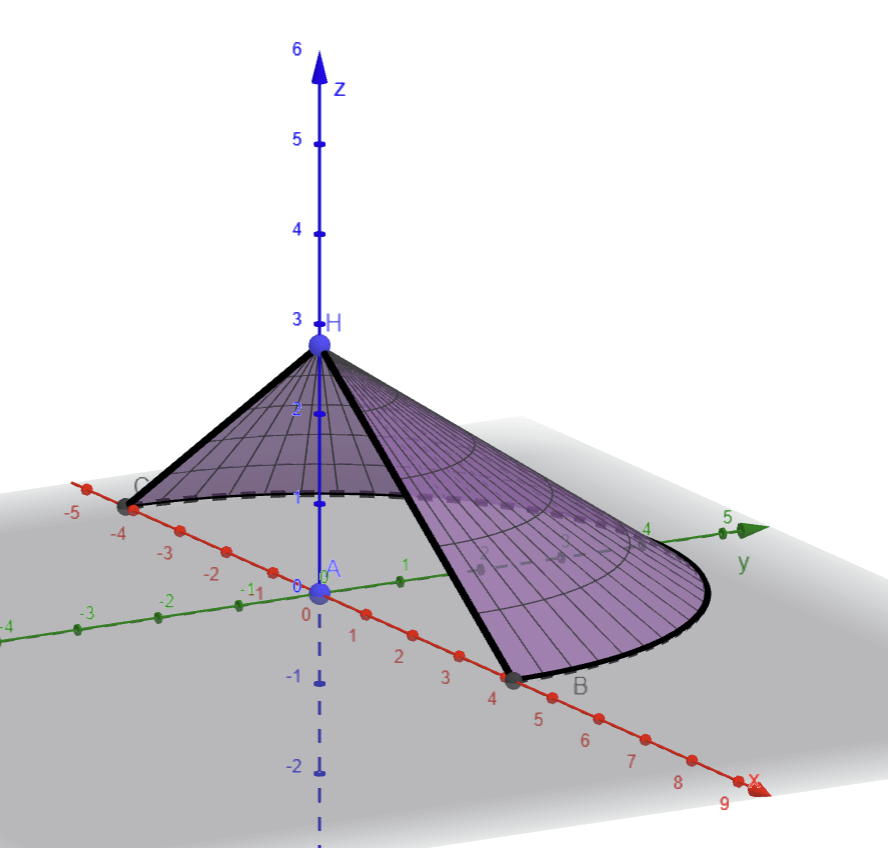## Résultat dans GeoGebra 3D  <center><em>Réal. Figures par Carole LE BELLER</em></center> </br> Fichier : https://www.geogebra.org/m/xzvsrreh --- --- # Étape 2️⃣ : Construction du reste de la modélisation 3D dans GeoGebra 3D ## Éléments de code GeoGebra 3D avec commentaires Saisir ligne par ligne les codes suivants i: Droite(H,axeY) \\Droite parallèle à l'axe des ordonnées et passant par le point H D=Point(i) \\D un point libre sur i j: Droite(B,i) \\Droite parallèle à i passant par B p: Plan(B,H,D) \\Plan D_{1}=MilieuCentre(H,B) \\Milieu de [HB] k: Perpendiculaire(D_{1},p) \\Droite perpendiculaire au plan p et passant par D_D_{1} d: Cercle(B,3,k) \\ Cercle de centre B, de direction k et de rayon 3 e: Cercle(H,7,k) \\ Cercle de centre H, de direction k et de rayon 7 (4 + 3 = 7 cm) E=Intersection(j,d,2) \\ Point d'interction entre d et j F=Intersection(i,e,2) \\ Point d'interction entre e et i c_{1}=Segment(H,B,q1) \\ [HB] côté du polygone q1 e_{1}=Segment(E,F,q1) \\ [EF] côté du polygone q1 f_{1}=Segment(F,H,q1) \\ [FH] côté du polygone q1 p2=Segment(B,E,q1) \\ [BE] côté du polygone q1 q1=Polygone(H,B,E,F) **Puis par symétrie** pv: Plan(D,H,A) \\ Plan vertical passant par H q1'=Symétrie(q1,pv) \\ Symétrique du polygone q1 par rapport au plan vertical pv E'=Symétrie(E,pv) \\ Symétrique du point E par rapport au plan vertical pv Renommer la longueur e_{1} du segment [EF] : EF G=MilieuCentre(E,F) \\ Milieu de [EF] Créer un curseur angle nommé "angle" allant de 20° à 180° de pas 1° p': Rotation(p,-angle,EF) \\ Rotation du plan p par rapport à l'axe [EF] de (-angle°) l: Perpendiculaire(E,p') \\ Droite perpendiculaire à p' q: Cercle(E,4,l) \\ Cercle de centre E de direction la droite l et de rayon 4 s: Cercle(F,5,l) \\ Cercle de centre F de direction la droite l et de rayon 5 G=Intersection(s,q,1) \\ Point d'intersection entre les deux cercles t1=Polygone(E,G,F) \\ Triangle EGF t1'=Symétrie(t1,pv) \\ Triangle symétrie de EGF par rapport au plan vertical pv G'=Symétrie(G,pv) \\ Point symétrique de G par rapport au plan vertical pv ## Résultats <center> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_35b70a9a4e6ae87a38dc94141f9f5ab6.png" alt="Dans GeoGebra 2D, converti en png" width="50%"><img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_0b66726224195a3d3cfe2efa14a8a4b8.png" alt="" width="50%"> </center> <center><em>Réal. Figures par Carole LE BELLER</em></center> </br> ## Résultats sans les points, les droites et les plans En désaffichant les plans, les droites, on obtient la figure suivante. Puis n désaffichant certains points, certains segments et les axes du repère et le plan, on obtient la figure suivante. <center> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_4d6000b7a721b1ebeac1cfbad4f6100a.png" alt="Dans GeoGebra 2D, converti en png" width="50%"><img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_c55188b4cee679ff54a745e1a3b06612.png" alt="" width="50%"> </center> <center><em>Réal. Figures par Carole LE BELLER</em></center> </br> </br> Fichier : https://www.geogebra.org/m/hxs64kcs --- --- # Étape 3️⃣ : Exportation en STL à partir de GeoGebra De GeoGebra, pour exporter la figure 3D en STL, aller dans Fichier Exporter en.. Impression 3D (.stl) La fenêtre (à modifier) ci-après apparaît <center> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_aaac044faecfc88ebc5bb59e1e828612.png" alt="Dans GeoGebra 2D, converti en png" width="70%"></center> --- --- # Étape 4️⃣ : Amélioration du modèle 3D avant impression 3D En images *(copies d'écran par Carole LE BELLER)*, dans Builder3D, importer le modèle puis - **Réparer le modèle et le retourner** <center> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_25200ef87a56921eaaf6855d7e69cdee.png" alt="Copie d'écran de Builder3D" width="45%"> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_5e9c30abd8e43e673a2ee32b677929c3.png" alt="Copie d'écran de Builder3D" width="45%"> </center> </br> - **Placer une sphère sur la partie à retirer et 'soustraire' dans 'Objet' puis 'Modifier' à deux reprises** <center> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_abcfa30e0ee423f7f9a7a6a2fdfd153a.png" alt="Copie d'écran de Builder3D" width="45%"> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_5f0f86b7314a3c546c547131be37ad54.png" alt="Copie d'écran de Builder3D" width="45%"> </center> </br> <center> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_ffa8d0ef659c8f2999c67bd4606525fb.png" alt="Copie d'écran de Builder3D" width="50%"> </center> </br> - **Enregister au format STL** <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_51f8ca8966c53c9bad0fd8e0e2d2013c.png" alt="Copie d'écran de Builder3D" width="45.7%"> <img src="https://minio.apps.education.fr/codimd-prod/uploads/upload_31cf2cfcc32a2915444c42d4bf7be146.png" alt="Copie d'écran de Builder3D" width="45%"> </center> </br> </br> Fichier : https://digipad.app/nfs6/933763/art3d-print3d-clb-transat-angle68-repare-mod-position_lgnh3g55e7.zip --- --- # Étape 5️⃣ : Impression 3D du modèle 3D Prototype *Images à venir...*