# Activité : Création d'une étoile géométrique  ## Objectifs - Apprendre à tracer une étoile à cinq branches. - Comprendre la décomposition en facteurs premiers. - Explorer les connexions entre les mathématiques et l'art. ## Matériel - Feuille A4 - Compas - Règle - Rapporteur - Crayon ## Instructions 1. **Préparation de la feuille** - **Tracer** légèrement les diagonales de la feuille A4 pour trouver son centre. 2. **Tracé du cercle principal** - Avec le compas, **tracer** un cercle de 9 cm de rayon centré sur l'intersection des diagonales. 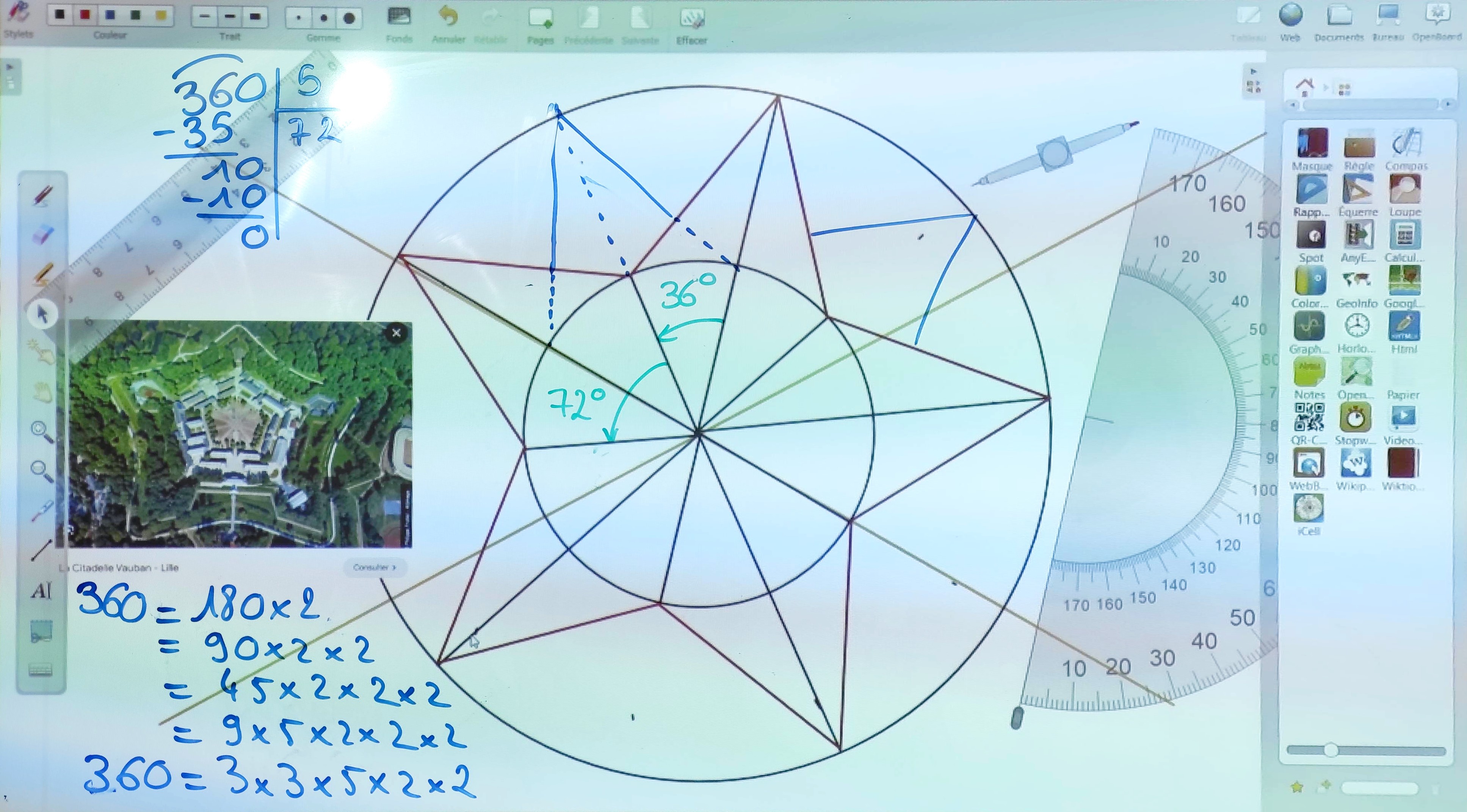3. **Décomposition en facteurs premiers de 360** - **Effectuer** la décomposition en facteurs premiers de 360 pour déterminer les options pour le nombre de branches. 4. **Choix du nombre de branches** - **Opter** pour un nombre de branches qui est un diviseur de 360 (par défaut 5). 5. **Division euclidienne de 360 par le nombre de branches** - **Calculer** l'angle entre les branches en divisant 360° par le nombre de branches choisi, par exemple 72° (puisque $360\div5 = 72$). 6. **Tracé des rayons** - **Utiliser** le rapporteur pour tracer des rayons du cercle tous les 72°. 7. **Tracé du second cercle** - En utilisant le même centre, **tracer** un second cercle de 4,5 cm de rayon à l'intérieur du premier. 8. **Bissectrices des branches** - **Tracer** des bissectrices à chaque paire de rayons pour délimiter les branches de l'étoile. L'angle entre la bissectrice et chaque branche doit être de 36° (pour l'étoile à 5 branches : $72\div2=36$). 9. **Construction de l'étoile** - **Relier** finalement les points où les bissectrices croisent le petit cercle pour former l'étoile à cinq branches. ## Approfondissement - Discutez de la possibilité de varier le nombre de branches en utilisant la décomposition en facteurs premiers de 360. - Évoquez les fortifications de Vauban et leur conception en étoile, faisant le lien entre géométrie et histoire. ## Conclusion Cette activité allie géométrie et créativité, enracinant les connaissances mathématiques dans des applications concrètes et historiques.